連続群論
連続群論
のぼりん さんの書込 (2006/08/22(Tue) 23:29)
こんにちは.私は社会人の物理ファンで,保江邦夫「連続群論」(日本評論社)を読んでいるところです.実は,他掲示板で疑問点を質問したのですが,回答が得られなかったため,ネットで検索し,こちらの存在を知りお邪魔しました.
さて,同書に,ヒルベルト空間 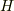 上の有界作用素
上の有界作用素 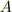 が正規作用素であることと,ある測度空間
が正規作用素であることと,ある測度空間  があって,あるユニタリ変換
があって,あるユニタリ変換 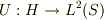 により
により
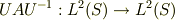
が  上の複素可測関数を乗じる線形作用素であることは同値である,という補題があります.その証明として,31 ページでは,
上の複素可測関数を乗じる線形作用素であることは同値である,という補題があります.その証明として,31 ページでは, 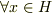 に対し,
に対し, 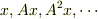 が張る閉部分空間
が張る閉部分空間 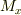 をヒルベルト空間と見ると,
をヒルベルト空間と見ると, 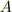 を
を 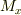 に制限した
に制限した 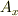 も
も 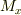 の自己共軛作用素になると説明しています.ここまでは判ります.これに引き続き同ページ 6 行目以下に
の自己共軛作用素になると説明しています.ここまでは判ります.これに引き続き同ページ 6 行目以下に
このとき 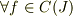 に対して写像
に対して写像
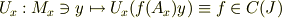
を定める.
との記述があります.しかしこれは, 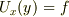 と定義する意図ではない筈です.おそらく何らかの誤植だろうと思うのですが,思い付きません.一体
と定義する意図ではない筈です.おそらく何らかの誤植だろうと思うのですが,思い付きません.一体 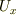 をどう定義する意味か,教えていただけますか?実際のところ,同書をお持ちでない人には説明が判り難いと思いますが,何卒よろしくお願いします.
をどう定義する意味か,教えていただけますか?実際のところ,同書をお持ちでない人には説明が判り難いと思いますが,何卒よろしくお願いします.
Re: 連続群論
toorisugari no Hiro さんのレス (2006/08/23(Wed) 00:02)
書かれていること自体ちんぷんかんぷんで,お役に立てそうにないですが,一応,お聞きします.
> このとき |468f76c79099426ce161714cc295045c| に対して写像 > |2bc42454f83aa19d0cb1b16d2e5ee948| >を定める.
に出てくる 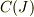 が何かわからないので教えてもらえませんか?
が何かわからないので教えてもらえませんか?
Re: 連続群論
のぼりん さんのレス (2006/08/23(Wed) 08:54)
toorisugari no Hiroさん:
早速のレス,どうもありがとうございます.^^感謝します.
ご指摘のとおり, 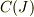 について,説明するのを失念していました.済みませんでした.
について,説明するのを失念していました.済みませんでした.
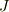 は実数上の閉区間で,
は実数上の閉区間で, ![J = [ - \parallel A \parallel, \parallel A \parallel]](http://hooktail.maxwell.jp/bbslog/af24dff944a32c75b78ece82cf8ffe37.png) と定義されています.ここに,
と定義されています.ここに, 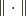 は 作用素ノルムです.
は 作用素ノルムです. 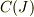 は,閉区間
は,閉区間 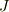 上の実連続関数全体の集合で,引用箇所の後に,恒等式
上の実連続関数全体の集合で,引用箇所の後に,恒等式
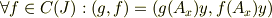
を示し,「 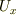 が有界な<b>等長線形作用素</b>となることがわかる.即ち
が有界な<b>等長線形作用素</b>となることがわかる.即ち 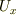 はヒルベルト空間
はヒルベルト空間 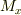 からヒルベルト空間
からヒルベルト空間 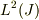 へのユニタリー変換を与える」としています.
へのユニタリー変換を与える」としています. 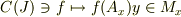 を
を 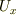 とするのならわかるのですが.しかし,
とするのならわかるのですが.しかし, 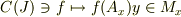 は単射でないので,これの逆写像を
は単射でないので,これの逆写像を 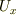 とすることはできませんし…
とすることはできませんし…
実は,著者のメール・アドレスをネット検索し,そこに問い合わせようとしたのですが,そのアドレスは有効でなく,万策尽きてしまいました.
何卒よろしくお願いします.
Re: 連続群論
toorisugari no Hiro さんのレス (2006/08/23(Wed) 10:18)
中身はまだ考えていないですが,
とりあえず,こちらの方
> 実は,著者のメール・アドレスをネット検索し,そこに問い合わせようとしたのですが,そのアドレスは有効でなく,万策尽きてしまいました.
メールアドレスはわかりませんが,ここに電話番号が書いてありますね.
Re: 連続群論
のぼりん さんのレス (2006/08/26(Sat) 06:52)
本件に関しては,自己解決しました. 結論的には,著者の混乱と思われます. どうもお騒がせしました.
しかし,この補題の証明には,本件以外にも(論理的に)おかしいところがあります. 読み続けるのが嫌になって来ました…
Re: 連続群論
mNeji さんのレス (2006/08/26(Sat) 10:25)
始めまして.
私は,のぼりんさんの勉強されている分野は判らないのですが,「独習者にとって,細かなところの記述にエラーがあった場合,とても苦労することがある」事に強く賛同いたします.
本に付いての疑問を受け付けない出版社も多く地団駄踏むことがあります.でも,一度は出版社にメールされることをお勧めします.私の経験では,海外にすむ著者に連絡を取っていただけたことがあります.
後一つのご提案としては,このスレッドに,のぼりんさんのお考えの「在るべき姿」をお書きになっては如何でしょうか? 少なくとも,誤回答ならば反応があるとおもいます.正解ならば,無回答の確率は高いかもしれませんが,同学の志をお持ちの方々に励みになると思います.ひいては,出版社や著者に反省を促すきっかけになるかもしれません.
是非とも,気持ちよく勉学・研究にお励み下されるように.
Re: 連続群論
のぼりん さんのレス (2006/08/26(Sat) 12:23)
mNejiさん,こんにちは. 励ましの言葉,ありがとうございました.
質問箇所そのものについては解決したのですが,実は証明の中身に疑問が生じ,今考えているところです. 第一感では,本書の方針には不備がある様に思われます. 自分なりの結論に至るまで一,二週間はかかりそうな雰囲気ですが,一応の結論が出たら,またこちらに報告します. 穴を埋められれば良いのですが,そうでなければ本書は断念せざるを得ないでしょう.
Re: 連続群論
のぼりん さんのレス (2006/08/27(Sun) 17:44)
本証明中の該当部分の主張は,たとえば恒等変換だと成り立たない様です. 同証明をどの様に変更すれば良いのか,判然としません. もっとも,補題の主張は,正規変換を対角化すれば良いことと考えます. 数学的な証明は兎も角,物理的には納得できたので,取り敢えず良しとします.
しかし,本書は読者にとって余り親切に書かれていない印象を受けています. そろそろ本書の諦めどきかも…
Re: 連続群論
Joh さんのレス (2006/08/28(Mon) 12:11)
のぼりんさん,私も同書を持っていましたが,いま手元に無いので返答しかねていました.確か,著者の人の自習ノートをそのまま本にしたものだったと思いますが,日本語が分かりにくかった印象があります.何か良い本をみつけたら,教えてください.
Re: 連続群論
のぼりん さんのレス (2006/08/29(Tue) 23:15)
Joh さん,こんばんは.著者の自習ノートですか!どおりで記述に穴が多い訳です.
元々量子力学の本を読んでいたところ,恥ずかしながらリー群の記述が良く判らず,進展が困難になってしまい,本書を買ってみました.元々リー群については余り知識がなく,私が読んだことがあるのは, ?山内,杉浦「連続群論入門」(培風館) ?松島与三「多様体入門」(裳華房) だけです.?は,三次元回転群,二次元特殊ユニタリ群,ローレンツ群等について解説しています.?は,リー群とリー環の基本事項について書いてあります.どちらも良い本だと思うのですが,これだけでは不足だと感じ,本書を読めば理解が深まるかと期待したのでしたが,甘かった様です.私こそ,何か良い本があったら,是非教えて下さい.
Re: 連続群論
toorisugari no Hiro さんのレス (2006/08/30(Wed) 00:07)
のぼりんさん: 中身については死んだ振りしてました._o_
> 私こそ,何か良い本があったら,是非教えて下さい.
洋書ですけど "Lie Algebras in Particle Physics" Howard Georgi
はどうでしょう.
物理屋がリー環の講義をするとき種本にする本だそうです. のぼりんさんの指向が純粋数学方面なのか物理方面なのかわかりませんが, 参考にされてはどうでしょう.
Re: 連続群論
のぼりん さんのレス (2006/09/02(Sat) 08:23)
toorisugari no Hiro さん
"Lie Algebras in Particle Physics" Howard Georgi を紹介いただき,ありがとうございました.アマゾンの紹介文を読んでみました.確かにしっかり勉強するにはとても良さそうな本ですね.生憎,今の私には少々荷が重そうですので,同書は将来の楽しみにとっておこうと思います.
Re: 連続群論
mNeji さんのレス (2006/09/02(Sat) 12:04)
横から失礼します.
ご紹介の本のamazon書評を拝見しました.こんなに好意的な意見が付いている本も珍しいと思います.特に最初の「エアコンさん」の;
>Lie代数を物理の人のために簡単に説明してくれています.けれど,見かけよりははるかに読むのが大変でした.それでも純粋な数学の本を読むよりは格段に読みやすいと思います. > > 個人的には装丁がとても気に入っています.フォント読みやすいです.愛着がわいて読んでいる期間は毎日持ち運んでいました.
には,微笑ましい光景を見た気がします.
#本の魅力の2つもが一緒になれば,いい本になる証拠だと思います.(LaTeX友の会・収集人 談)
群→結晶→物性→困難→遠のく のループから脱却できると,いいのですが.だれか「猫の脳をもった物理屋をして,Lie群を親しめるための講義」をしてくれませんかね.
Re: 連続群論
Chappy さんのレス (2006/09/02(Sat) 13:20)
僕もお邪魔します,,,Chappyです.. Lie群ではないですが,Lie代数の本なら, “リー代数入門佐藤肇”がいいですよ,mNejiさん. 楽しく計算しながら,学べる感じです.線形代数は必須ですが. 定義,定義,補題,補題,定理,定義,,,などと追い込まれることはないですよ. けっこう簡単な言葉で書いてあるのに,意外にもやってることは深かったりします. 僕も読んでる途中なので,mNejiさんもぜひ!!
Re: 連続群論
mNeji さんのレス (2006/09/02(Sat) 16:29)
Chappyさん:
> Lie群ではないですが,Lie代数の本なら,
てっきり別物かと思っていました.
>楽しく計算しながら,学べる感じです.線形代数は必須ですが. 複素数の計算なら,チト興味深いですね.でも線形代数といわれると難しそう.
>定義,定義,補題,補題,定理,定義,,,などと追い込まれることはないですよ. 「追い込まれる」っそ,そうなんです,数学の本は....
さらに付け加えさせていただくと,最初の数ページに無茶苦茶難しい記号などが撒き散らしてあって,それを無視して読むと突然に簡単になったりして.若い頃は,この手のコケ脅かしで,踵を返したのだろうと思います.
>けっこう簡単な言葉で書いてあるのに,意外にもやってることは深かったりします. う〜む,専門の学生さんがそこまで言うのですから,一度は見てみようかとおもいます.
そういえば,授業でSU(2),SU(3)に入っても,抽象論が延々と続き,表現論の論議でうとうとしてたら,チクチクと皮肉られたのを,思い出してしまった.
でも,それらの発展かと思うと,親近感も出てきますね.
Re: 連続群論
Joh さんのレス (2006/09/02(Sat) 23:19)
Chappyさん,
それって,「線形代数の続きとして」とか書いてある,割と薄い本ですか? そういえば夏休みにキリング形式とか計算してましたよね.
うーん,取り組んでみようかなぁ.
Re: 連続群論
Chappy さんのレス (2006/09/02(Sat) 23:59)
>mNejiさん 抽象論の中にちゃんと具体例を見出していれば,mNejiさんにとってその授業も楽しいでしょうね.初対面から,綺麗で完璧すぎる構築物を見せられるから,数学の講座に眠気(吐き気?)が出てくるのかもしれませんね (^^; 時間の都合上,仕方ないのかもしれません. でも,幸せですよ.今までの数学の歴史の集大成の一部を,たった 1時間半30分×14 の時間の中で習えるんですから.かなりのスピードのジェットコースターです.それだけの歴史の重み,簡単に理解できなくて当たり前と思うことにしましょう(笑)
>Johさん それです,それ!ご存知でしたか,,, Johさんには物足りないのではないですか??
僕は,数学のカリキュラムに「線形代数の続きとしてのLie代数入門」という講座を作ってもよいのではないかと思います.教養の講座でもできるでしょう.線形代数の復習と理解にぴったりだと思います.きっと著者の佐藤肇先生は名大でそんな講座を開いているのだろうとは思いますが.
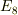 行列なんてホットなところですね.
行列なんてホットなところですね.
Re: 連続群論
のぼりん さんのレス (2006/09/06(Wed) 21:43)
事後報告です.
toorisugari no Hiro さんにご紹介いただいた Howard Georgi の「Lie Algebras in Particle Physics」を,ついアマゾンで買ってしまい,本日届きました. 読まなければいけない本がどんどん増えて,困り果てています.(笑)
Re: 連続群論
toorisugari no Hiro さんのレス (2006/09/06(Wed) 22:31)
> 読まなければいけない本がどんどん増えて,困り果てています.(笑)
(^^).まったく御意.
こんど,読後感をのせてください.
Re: 連続群論
mNeji さんのレス (2006/09/06(Wed) 23:31)
>読まなければいけない本がどんどん増えて,困り果てています.(笑)
嬉しい悲鳴ですね.
>こんど,読後感をのせてください.
と言わずに,読みながらの質問の方が,双方の為では?
Chappyさんも「リー代数入門」の資料を基に解説をする模様?
こんなに摩訶不思議に人を引き付けるものは何だろうという素朴な興味もありますので,是非とも宜しくお願いします.
Re: 連続群論
のぼりん さんのレス (2006/09/09(Sat) 16:35)
本書の前に読むべき本が山積みになっていますので,何時になったら本書に到達できることやら… まぁ,こんな状態ですが,いつか本書に到達したら経過報告を致します.