トンネル確率計算

トンネル確率計算

ムー民 さんの書込 (2006/08/21(Mon) 11:59)

はじめまして，現在大学４年のムー民と申します．質問させていただきたいのですが，量子力学，トンネル確率の計算は，どうやって計算すればいいのでしょうか．障壁を越えた後との振幅の比までは何とか出せるのですが…その後，その比の絶対値の２乗を求めることが計算が複雑すぎてできません．Re項とIm項にわけ，それぞれ２乗して出す方法を使用しているのですが，もっと簡単に求める方法はないのでしょうか？何か方法ありましたらぜひ教えていただきたく思います．

Re: トンネル確率計算

mNeji さんのレス (2006/08/21(Mon) 13:19)

具体的にどんなポテンシャルを考えて，どんな波動関数を仮定して解いたとかを書けますか？

恐らく，1次元で計算されているのでしょうから，常微分方程式ですよね？適当にテキスト形式で書いてくだされば，LaTeXには変換しますよ．

Re: トンネル確率計算

ムー民 さんのレス (2006/08/21(Mon) 13:38)

mNeji様返信ありがとうございます．本当にごく一般的な障壁のトンネル確率です．一次元で0<x<aの範囲で，ポテンシャルがV，それ以外では０で，E<Vの場合を考えています．（本当に一般的な教科書に載っているようなものです．）障壁を越えた後の振幅をF，越える前の前進波の振幅をAとして， F/A={4κk*exp(κ-ik)a}/{(κ+ik)^2+(κ-ik)^2*exp(2κa)} ただしk^2=2mE/h^2,κ=2m(V-E)/h^2 というような感じです． ここから｜F/A|^2を求めたいのですが，まず分母を有理化のように実数に変えて，そのあとReとImを分けて２乗するという方法でやろうとしたのですがあまりにも計算が面倒で，（大学院の試験中にやるような計算ではないような…）困っていました．ほかにもさまざまな場面でこのような計算をする機会があるかとは思いまして，簡単な計算方法があるのではと思ったのですが… 困ったことに何冊かの教科書を探してみても途中の計算過程を書いてくれているものはなかったので… つまらない質問でお手数をおかけしまして大変申し訳ありません．

Re: トンネル確率計算

mNeji さんのレス (2006/08/21(Mon) 14:45)

すいません，量子力学に付いては，まだ記憶が蘇えっていないので，考え方がまだ明確でないので直ぐにお答えできません．

でも，1次元の跳び箱型のポテンシャル問題ですから，計算は出来るはずですね．

むしろ，直ぐに振幅の話をされていますが，計算する上では，全ての計算過程を明示するべきと思います．どこかでミスをしていると，計算を検証することが出来ないからです．

そこで，波動関数を跳び箱の，左側，その中，右側でどのように設定して，それぞれの波動関数をどのような条件で連結したかを明示した上で，必要な状態量の計算を明記しませんか？

複素数の計算に持ち込めば，なんどか答えは導き出ると思います(指先パワーです：笑).

Re: トンネル確率計算

mNeji さんのレス (2006/08/21(Mon) 15:34)

直接の答えは書いてありませんが，丁寧な解説として,

● 初等量子力学／量子力学（2004年度講義録）

がありました．

さてご質問を図にすると

<pre>

《図1 ポテンシャルと波数》

V ＿＿＿ ＿＿＿＿＿＿＿＿__ V ↑｜｜ ｜｜｜ ｜｜｜ E ＿＿＿＿｜｜｜ ↑｜｜ ｜｜｜ ｜｜｜ ＿＿＿＿｜＿＿＿＿＿＿＿＿＿｜｜＿＿＿＿＿＿＿＿＿

x＝0 x=a

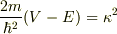
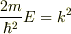
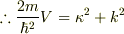
\frac{2m}{\hbar^2}(V-E)=\kappa^2 \frac{2m}{\hbar^2}E=k^2 \therefore \frac{2m}{\hbar^2}V=\kappa^{2}+k^2

《図2ポテンシャルと波動関数》

＋――――――――＋ V ｜｜

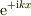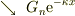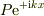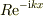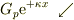\ \mathrm{e}^{+\mathrm{i}kx} →｜ \searrow \ G_{n}\mathrm{e}^{-\kappa x} ｜ \ P\mathrm{e}^{+\mathrm{i}kx} → \;\ \;R\mathrm{e}^{-\mathrm{i}kx}\ ←｜ \ \; G_{p}\mathrm{e}^{+\kappa x}\ \swarrow ｜ ｜｜ ＿＿＿＿＿＿＿＿＿＿＿＿＿＿｜｜＿＿＿＿＿＿＿＿＿

x＝0 x=a

1) 左の領域2) 中央の領域3) 右の領域 右向き進行波 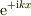\ \mathrm{e}^{+\mathrm{i}kx} 右向き減衰波 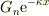\ G_{n}\mathrm{e}^{-\kappa x} 右向き進行波 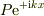\ P\mathrm{e}^{+\mathrm{i}kx} 左向き反射波 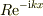\ R\mathrm{e}^{-\mathrm{i}kx} 左向き減衰波 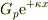\ G_{p}\mathrm{e}^{+\kappa x} </pre>

●波動関数とその導関数についての連続性

・ｘ＝０で

1+R =G_{n} + G_{p} \tag{1}
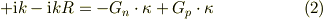
+\mathrm{i}k-\mathrm{i}kR=-G_{n}\cdot \kappa + G_{p}\cdot \kappa \tag{2}

・ｘ＝a で

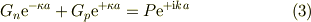
G_{n}\mathrm{e}^{-\kappa a} + G_{p}\mathrm{e}^{+\kappa a}=P\mathrm{e}^{+\mathrm{i}k a} \tag{3}
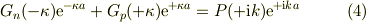
G_{n}(-\kappa)\mathrm{e}^{-\kappa a} + G_{p}(+\kappa)\mathrm{e}^{+\kappa a}=P(+\mathrm{i}k)\mathrm{e}^{+\mathrm{i}k a} \tag{4}

●係数を求める

波動関数の係数 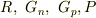R,\ G_{n},\ G_{p},P は4個で，波動関数の接続条件も4本の一次式だから解く事ができる．

大雑把にいえば，(1),(2)からRを消去し，(3),(4)からPを消去し，それらから 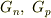G_{n},\ G_{p} を求め，それらからR,Pを求める．

(1)*(ik)+(2)

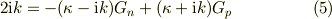
2\mathrm{i}k=-(\kappa -\mathrm{i}k)G_{n}+(\kappa +\mathrm{i}k)G_{p} \tag{5}

(3)*(ik)-(4)

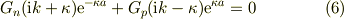
G_{n}(\mathrm{i}k +\kappa)\mathrm{e}^{-\kappa a} +G_{p}(\mathrm{i}k -\kappa)\mathrm{e}^{\kappa a}=0 \tag{6}

上式から，直ちに

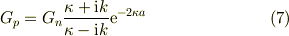
G_{p}=G_{n}\frac{\kappa +\mathrm{i}k}{\kappa -\mathrm{i}k}\mathrm{e}^{-2\kappa a} \tag{7}

(5)に代入し，

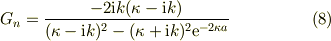
G_{n}=\frac{-2\mathrm{i}k(\kappa -\mathrm{i}k)}{(\kappa -\mathrm{i}k)^2-(\kappa +\mathrm{i}k)^2\mathrm{e}^{-2\kappa a}} \tag{8}

(7)に代入して

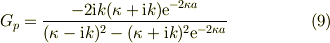
G_{p}=\frac{-2\mathrm{i}k(\kappa +\mathrm{i}k)\mathrm{e}^{-2\kappa a}}{(\kappa -\mathrm{i}k)^2-(\kappa +\mathrm{i}k)^2\mathrm{e}^{-2\kappa a}} \tag{9}

(8),(9)の右辺を見ると,分母・分子に 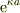\mathrm{e}^{\kappa a} を掛けると，指数関数が対称的になることがわかる．また，分母を実部・虚部とに整理する．

(9)から始める，

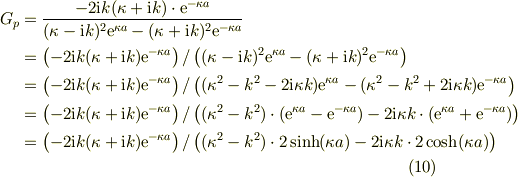
G_{p}&=\frac{-2\mathrm{i}k(\kappa +\mathrm{i}k)\cdot\mathrm{e}^{-\kappa a}}{(\kappa -\mathrm{i}k)^{2}\mathrm{e}^{\kappa a}-(\kappa +\mathrm{i}k)^2\mathrm{e}^{-\kappa a}}\\&=\left(-2\mathrm{i}k(\kappa +\mathrm{i}k)\mathrm{e}^{-\kappa a}\right) /\left( (\kappa -\mathrm{i}k)^{2}\mathrm{e}^{\kappa a}-(\kappa +\mathrm{i}k)^2\mathrm{e}^{-\kappa a} \right)\\&=\left(-2\mathrm{i}k(\kappa +\mathrm{i}k)\mathrm{e}^{-\kappa a}\right) /\left( (\kappa^2 -k^2 -2\mathrm{i}\kappa k)\mathrm{e}^{\kappa a}-(\kappa^2 -k^2 +2\mathrm{i}\kappa k) \mathrm{e}^{-\kappa a} \right) \\&=\left(-2\mathrm{i}k(\kappa +\mathrm{i}k)\mathrm{e}^{-\kappa a}\right) /\left( (\kappa^2 -k^2 )\cdot(\mathrm{e}^{\kappa a}-\mathrm{e}^{-\kappa a})-2\mathrm{i}\kappa k \cdot(\mathrm{e}^{\kappa a}+\mathrm{e}^{-\kappa a}) \right) \\&=\left(-2\mathrm{i}k(\kappa +\mathrm{i}k)\mathrm{e}^{-\kappa a}\right)/ \left( (\kappa^2 -k^2 )\cdot 2\sinh(\kappa a) -2\mathrm{i}\kappa k \cdot2\cosh(\kappa a) \right) \tag{10}

同様な処理を(8)について実施すると

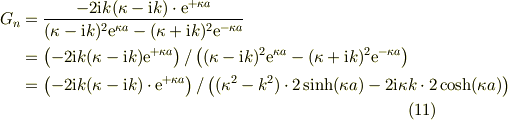
G_{n}&=\frac{-2\mathrm{i}k(\kappa -\mathrm{i}k)\cdot \mathrm{e}^{+\kappa a}}{(\kappa -\mathrm{i}k)^{2}\mathrm{e}^{\kappa a}-(\kappa +\mathrm{i}k)^2\mathrm{e}^{-\kappa a}} \\&=\left(-2\mathrm{i}k(\kappa -\mathrm{i}k)\mathrm{e}^{+\kappa a}\right) /\left( (\kappa -\mathrm{i}k)^{2}\mathrm{e}^{\kappa a}-(\kappa +\mathrm{i}k)^2\mathrm{e}^{-\kappa a} \right)\\&=\left( -2\mathrm{i}k(\kappa -\mathrm{i}k)\cdot \mathrm{e}^{+\kappa a} \right)/\left( (\kappa^2 -k^2 )\cdot 2\sinh(\kappa a) -2\mathrm{i}\kappa k \cdot2\cosh(\kappa a) \right)\tag{11}

(10),(11)を(3)に代入すると，

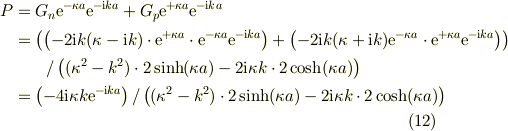
P &=G_{n}\mathrm{e}^{-\kappa a}\mathrm{e}^{-\mathrm{i}k a} + G_{p}\mathrm{e}^{+\kappa a} \mathrm{e}^{-\mathrm{i}k a} \\&=\left(\left( -2\mathrm{i}k(\kappa -\mathrm{i}k)\cdot \mathrm{e}^{+\kappa a} \cdot \mathrm{e}^{-\kappa a}\mathrm{e}^{-\mathrm{i}k a} \right) + \left( -2\mathrm{i}k(\kappa +\mathrm{i}k)\mathrm{e}^{-\kappa a}\cdot \mathrm{e}^{+\kappa a} \mathrm{e}^{-\mathrm{i}k a} \right) \right) \\& \qquad / \left((\kappa^2 -k^2 )\cdot 2\sinh(\kappa a) -2\mathrm{i}\kappa k \cdot2\cosh(\kappa a)\right) \\&=\left( -4\mathrm{i}\kappa k \mathrm{e}^{-\mathrm{i}k a} \right)/ \left( (\kappa^2 -k^2 )\cdot 2\sinh(\kappa a) -2\mathrm{i}\kappa k \cdot2\cosh(\kappa a)\right)\tag{12}

(10),(11)を(1)に代入すると，

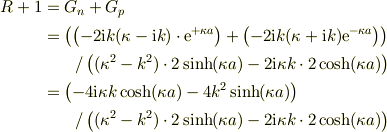
R+1 &=G_{n} + G_{p} \\&=\left(\left( -2\mathrm{i}k(\kappa -\mathrm{i}k)\cdot \mathrm{e}^{+\kappa a} \right) + \left( -2\mathrm{i}k(\kappa +\mathrm{i}k)\mathrm{e}^{-\kappa a} \right) \right) \\& \qquad / \left((\kappa^2 -k^2 )\cdot 2\sinh(\kappa a) -2\mathrm{i}\kappa k \cdot2\cosh(\kappa a) \right) \\&=\left( -4\mathrm{i}\kappa k \cosh(\kappa a) -4k^2 \sinh(\kappa a) \right) \\& \qquad / \left((\kappa^2 -k^2 )\cdot 2\sinh(\kappa a) -2\mathrm{i}\kappa k \cdot2\cosh(\kappa a)\right)

上式を整理して，

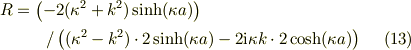
R &=\left(-2(\kappa^2 + k^2)\sinh(\kappa a) \right) \\& \qquad / \left((\kappa^2 -k^2 )\cdot 2\sinh(\kappa a) -2\mathrm{i}\kappa k \cdot2\cosh(\kappa a)\right)\tag{13}

● 検討と検算

今回のモデルは，十分遠方の左側から進行波が振幅1で入射し，原点で振幅Rで反射(reflection)し，ポテンシャル障壁を負のエネルギーにより減衰しながら通りぬけ，再度，透過(penetration)して再度振幅Pの進行波として前方に散乱する．

したがって，反射係数|R|^2や透過係数|P|^2を求めると，その和は1にならないといけない．

これらを計算するのに，(12),(13)の分母 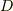D の|D|^2を求めておく．

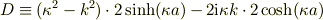
D \equiv (\kappa^2 -k^2 )\cdot 2\sinh(\kappa a) -2\mathrm{i}\kappa k \cdot2\cosh(\kappa a)
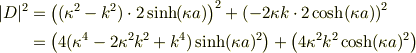
|D|^2 &= \left( (\kappa^2 -k^2 )\cdot 2\sinh(\kappa a) \right)^2 + \left( -2\kappa k \cdot2\cosh(\kappa a) \right)^2 \\&= \left( 4(\kappa^4 -2\kappa^2 k^2 +k^4 )\sinh(\kappa a)^2 \right) + \left( 4\kappa^2 k^2\cosh(\kappa a)^2 \right)

ここで 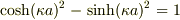\cosh(\kappa a)^2 -\sinh(\kappa a)^2 =1 に注意すると

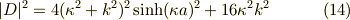
|D|^2 = 4(\kappa^2 +k^2)^2 \sinh(\kappa a)^2 +16\kappa^2 k^2 \tag{14}

(12)と(14)より,透過確率は

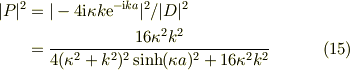
|P|^2 &=|-4\mathrm{i}\kappa k \mathrm{e}^{-\mathrm{i}k a}|^2 / |D|^2 \\&= \frac{16\kappa^2 k^2}{4(\kappa^2 +k^2)^2 \sinh(\kappa a)^2 +16\kappa^2 k^2} \tag{15}

(13)と(14)より,反射確率は

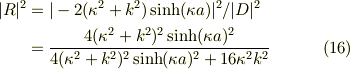
|R|^2 &=|-2(\kappa^2 + k^2)\sinh(\kappa a) |^2 / |D|^2 \\&= \frac{4(\kappa^2 + k^2)^2 \sinh(\kappa a)^2}{4(\kappa^2 +k^2)^2 \sinh(\kappa a)^2 +16\kappa^2 k^2} \tag{16}

(15),(16)は「透過確率＋反射確率=1」を満たすことが確認された．

なお，図1で示した関係；

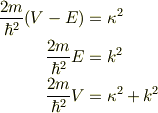
\frac{2m}{\hbar^2}(V-E) &=\kappa^2 \\\frac{2m}{\hbar^2}E &=k^2 \\\frac{2m}{\hbar^2}V &=\kappa^{2}+k^2

で各確率を書き下すと；

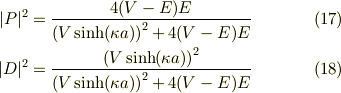
|P|^2 &= \frac{4(V-E)E}{\left(V \sinh(\kappa a)\right)^2 +4(V-E)E} \tag{17}\\|D|^2 &= \frac{\left(V \sinh(\kappa a)\right)^2}{\left(V \sinh(\kappa a)\right)^2 +4(V-E)E}\tag{18}

(18)式が判り易いですが，ポテンシャル・障壁が高くなると反射係数が大きくなり，極限で1となり透過出来ない事になります．

他方，ポテンシャル・障壁Vが低くなって，入射エネルギEに近づいても，一気にゼロにならないところが面白いですね．

いま，この説明を書いていて気になってきたのですが，この逆に，井戸型のポテンシャルだったらどういう挙動をするのでしょうかね．落ち着いたら解いてみてください．

Re: トンネル確率計算

toorisugari no Hiro さんのレス (2006/08/21(Mon) 17:07)

量子力学しばらくといてないので，大ぼけかもしれませんが， 右の領域の波数は1ではなく k にすべきでは?

Re: トンネル確率計算

mNeji さんのレス (2006/08/21(Mon) 18:01)

>右の領域の波数は1ではなくkにすべきでは?

仰せの通りだと思います．訂正いたしました．

つい，アスキー・アートに目が...いっその事，LaTeXで，アスキー・アートが出来たらいいのですが(笑)．

Re: トンネル確率計算

ムー民 さんのレス (2006/08/21(Mon) 20:21)

ｍNeji様の返信（No11432）のとおりの条件です．境界条件はｘ＝aにおいて関数が一致することと，その微分も連続であることが条件です．それらの条件からMnejiさんの記述で言えば１／Pが求まります． これが最初の投稿で記述した F/A={4κk*exp(κ-ik)a}/{(κ+ik)^2+(κ-ik)^2*exp(2κa)} になります．この計算結果は教科書にも載っていますのであっていると思います． あとはこの|F/A|^2を求めればいいわけですが… やはりここからは指先パワーですかね（笑） 根気よくゴリゴリ計算してみようと思います．皆様いろいろご意見ありがとうございました．実は院試まであと６日しかないので…(>_<)間に合いません笑．大変勝手ながら失礼いたします． ありがとうございました．

Re: トンネル確率計算

mNeji さんのレス (2006/08/21(Mon) 21:07)

ムー民さん：

了解しました．なにはともあれ，ベストを尽くしてください．

自分の推量だけで書いてしまい，自信がなくなったので，細かく検索しました．その結果ずばりの計算をされている方を拝見できました．

トンネル効果(1次元)

取り急ぎ，ご連絡まで．

自分は，時間が掛かりそうですが，指パワーによって算出してみますが，時間が掛かりそうです．判ったら，書き入れます．

試験は，時間との格闘ですが，開き直って「自分の理性によって判らぬものは無いのだ！」と心を落ち着かせて，ベストを尽くされますように．

そういう意味では，障壁の透過確率の解法過程が見つかったのは，首尾のよい兆候だと感じます．

Re: トンネル確率計算

mNeji さんのレス (2006/08/22(Tue) 22:42)

計算結果を No.11432 に示しました．

ムー民さんの途中経過や，他のサイトの結果とも微妙に食い違いが在るようですが，ゴーイング・マイ・ウェイで作って見ました．

細かな検算はサボっていますが，「透過確率と反射確率の和が１」となる事は確認しました．

将来,時間ができたら検算をして，結果をお知らせくださると，嬉しいです．

量子力学の演習なんて考えると，こんなにつまらない計算も無いですが，「指パワーの訓練や，量子力学クイズ」と考えれば善い事に気づきました(笑)．

追伸：

改めて

と比較したところ，一致しています．でも，なんで透過確率と反射確率を判りにくく書くのだろうか？ どこかに底本があるのかもしれないな．

Re: トンネル確率計算

toorisugari no Hiro さんのレス (2006/08/23(Wed) 01:21)

mNejiさま: 計算ご苦労様です．昔解いたと思っているんですが，こんなに大変だったんですね．(たぶん，最後まで解かず途中でごまかしてたんでしょうね．)

(10,11)式

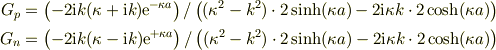
G_{p}&=\left(-2\mathrm{i}k(\kappa +\mathrm{i}k)\mathrm{e}^{-\kappa a}\right) / \left( (\kappa^2 -k^2 )\cdot 2\sinh(\kappa a) -2\mathrm{i}\kappa k \cdot2\cosh(\kappa a) \right)\\G_{n}&=\left( -2\mathrm{i}k(\kappa -\mathrm{i}k) \mathrm{e}^{+\kappa a} \right)/\left( (\kappa^2 -k^2 )\cdot 2\sinh(\kappa a) -2\mathrm{i}\kappa k \cdot2\cosh(\kappa a) \right)

これをこのまま変形するより

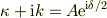
\kappa + \mathrm{i}k = A\mathrm{e}^{\mathrm{i}\delta/2}

とおいた方が「若干」計算が楽になります．(いや，本質的には楽にならないかも．．．)

ちなみに

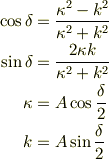
\cos\delta &= \frac{\kappa^2-k^2}{\kappa^2+k^2}\\\sin\delta &= \frac{2\kappa k}{\kappa^2+k^2}\\\kappa &= A\cos{\frac{\delta}{2}}\\k &= A\sin{\frac{\delta}{2}}

です．

Re: トンネル確率計算

mNeji さんのレス (2006/08/23(Wed) 01:46)

toorisugari no Hiroさん：

私は，量子力学は夏休みの宿題で朝永振一郎さんの「量子力学I・II」を読まされた以外は，ファインマンの量子力学しか読みませんでした．なので，こんな面倒な問題は絶対解いたことありません．もしヤッテイタラ今回解かなかったと思います．

でも，下手な波動の問題を無理に解くよりは，シンプルでイメージを確り持てて，いい問題だと思いました．そこで「仮想のポテンシャル・バリアをシリコン・チップ上に構築して，そこに電子をぶつける」として具体的に，波動関数を作図すると面白いかと思ってます．

もし，具体的にそんな感じの解説をした本をご存知ではありませんか？

Re: トンネル確率計算

toorisugari no Hiro さんのレス (2006/08/23(Wed) 02:00)

> もしヤッテイタラ今回解かなかったと思います．

御意．

> そこで「仮想のポテンシャル・バリアをシリコン・チップ上に構築して，そこに電子をぶつける」として具体的に，波動関数を作図すると面白いかと思ってます．

この問題は本当は波束で考えなければいけないと，本か教官がいってた気がします． でも，そうなると手計算ではダメで，シミュレーションでやるしかないでしょうね．

> もし，具体的にそんな感じの解説をした本をご存知ではありませんか？

ごめんなさい．私は知りません．

Re: トンネル確率計算

mNeji さんのレス (2006/08/23(Wed) 10:04)

toorisugari no Hiroさん：

>この問題は本当は波束で考えなければいけないと，本か教官がいってた気がします． >でも，そうなると手計算ではダメで，シミュレーションでやるしかないでしょうね．

物理の面白さの一つには，シンプルな模型で大筋の理解をして上で，重要なポイントを攻略することかもしれませんね．

こういう量子力学の散乱問題があるから，高校の物理で「波動」を教えるのかと思い至りました．でも，量子力学では波動方程式を前面において論議できるので，「物理の部分」と「計算の部分」が明快にできて説明も楽ですね．

他方,高校の物理で，「クントの実験」を明快にすればするほど，「物理の問題」だけが鮮明になってしまって，たんなるショーに終わる危険性があると思いました．

やはり高校の物理には「波動」は無用である，と思いました...．

追伸：

こんなところで，cosh(x)^2 - sinh(x)^2 =1 ，のお世話になるとは思いませんでした.途中，「cosh(x)^2 ＋ sinh(x)^2 =1」としたために．とても変な感じになり，大慌てしました．結局，指数表現に戻って，気が付きました(爆笑)．やはり指数関数は偉大ですね．

Re: トンネル確率計算

mNeji さんのレス (2006/08/23(Wed) 12:05)

近似で調べていたら，

次のサイトで

電子顕微鏡 基本用語集

次の項目がありました，商品(電子顕微鏡)の説明に，平面波ボルン近似の説明を見るとは思いもしませんでした．

ーーーーーーーーーー引用ーーーーーーーーーーーーーーー ボルン近似 Born approximation

結晶による電子の散乱を考えてシュレーディンガー方程式を解くとき，電子線のエネルギーが相互作用のポテンシャルエネルギーに比べて大きい場合，相互作用を摂動とみなし散乱波を冪級数展開して最低次の項を取る近似．具体的には，散乱波を摂動がないときの解である平面波に対する微小な付加項としてシュレーディンガー方程式を解く．ボルン近似で結晶構造因子が結晶ポテンシャルのフーリエ変換で与えられる．→結晶構造因子

Re: トンネル確率計算

mNeji さんのレス (2006/09/11(Mon) 03:00)

ムー民さん：

もうご覧になっていないと思いますが，この記事の計算は馬鹿正直にする人は少ないと思いますので，記事として保存する作業を始めたいと思います．

もし何か困る点があればご連絡ください．

作業は，明示的に反対が無ければ，進行したいとおもいます．

以上

上記のご連絡をしたあと，「かぎプロジェクト」で記事に変換作業を始めたのですが，ある都合で作業の続行が出来なくなりました．

資料のバックアップはさせていただいてますので，事情が許せば何らかの方法で，ご質問と，回答をあわせて公開し，今後の勉強家の学生さんに説明できるようにしたいとおもいます．

取り急ぎ，お詫びもうしあげます．

2006-09-16 16:06 mNeji