手に馴染むLaTeXe #01
手に馴染むLaTeXe #01
mNeji さんの書込 (2006/08/20(Sun) 01:10)
これまで,下記のスレッドで多くの論議を戴き有難うございました.
---- 記 ----- 「数学用語の使い方」と「TeXでの表し方」 - 2006/08/04(Fri) 20:16 No.11108"
ただし,一つのスレッドが長いと,他のスレッドをご覧になる方を妨害するらしいので,あらたなスレッドに切り替えたいと思います.
此処では,前回のスレッドで浮き上がってきたLaTeXにより「数学,物理,化学,工学などの分野での数式表現」を「効率よく・豊かな表現力を保ち,手に馴染む」にはどうすればいいのかを論議していただけたらと思います.
なお,スレッドの投稿数が20ぐらいをを目安に,スレッドを更新したいと思います.長丁場の論議なので,気の向いたら,お好きな論議を下されば嬉しいです.
Re: 手に馴染むLaTeXe #01
toorisugari no Hiro さんのレス (2006/08/29(Tue) 22:21)
No.11132
■7■ ベクトル
の記事ですが,
変数としての太字のベクトル表記にはmathbfよりboldsymbolが良いと思います.(ただし, 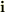 にはどちらがよいかわかりません.)
にはどちらがよいかわかりません.)
<Tex>mathbf{A}, boldsymbol{A}</Tex>
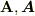
Re: 手に馴染むLaTeXe #01
mNeji さんのレス (2006/08/29(Tue) 23:05)
ご意見有難うございます.
現在,他の記事と同じフォーマットに変換するべく準備中です.
その中で判ったことをご報告します.
太字ベクトルについては bm というのがこのサイトに準備されているようです.
<Tex>mathbf{A}, boldsymbol{A}, bm{A}, boldmath{A}, xbm{i}+ybm{j} </Tex>
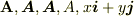
#おっと,こうやって見ると,bmは boldsymbolに近いですね.
基底ベクトルも bm としようかと思います.理由は,基底ベクトルだからといって,特殊な関数でも,固有名詞でもないベクトル変数と考えました.
ここら辺,お気づきの点は,どしどしお教えくださるとありがたいです.
====
あいう"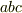 "かき
"かき
Re: 手に馴染むLaTeXe #01
toorisugari no Hiro さんのレス (2006/08/30(Wed) 00:14)
mNeji様:
ふむ.bm,よさげですね.こっちの方がいいと思います.
> 基底ベクトルも \bm としようかと思います.
賛成します.系の回転で基底ベクトルの中身(??)は変わるので斜体の方がいいと思います.
Re: 手に馴染むLaTeXe #01
mNeji さんのレス (2006/08/30(Wed) 02:16)
toorisugari no Hiroさん:
>賛成します.系の回転で基底ベクトルの中身(??)は変わるので斜体の方がいいと思います.
有難うございます,ほっとします.
他方,自分の好みで言えば,どうしても,上に矢印か横棒が無いとヴェクタに見えなくて...,でも横棒は複素数に取られてしまったので,矢印しか残らなくって....
で,突然気になりだしたのですが,学生の頃,書くのが嫌いで
・ベクトル 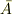 ・複素共役
・複素共役 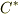 ・余弦
・余弦 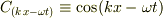
試験の時は,ベクトルと三角関数は定義をして解答してました(笑).
Re: 手に馴染むLaTeXe #01
MXK さんのレス (2006/08/31(Thu) 19:12)
ベクトルを(斜体)太字にするのは賛成です. 高校生は矢印で習っているようですが.
あと,cos, sin の引数に括弧がついているのが気になりました. 1つの項しかない場合は省略するのが一般的です. cosh なども同様です.
2階微分のところのダッシュが足りません.
Re: 手に馴染むLaTeXe #01
mNeji さんのレス (2006/08/31(Thu) 22:12)
MXKさん:
ご意見有難うございます.
>ベクトルを(斜体)太字にするのは賛成です. >高校生は矢印で習っているようですが.
私は,高校のときにベクトルは習わなかったと思います.大学でベクトルを勉強したときはベクトルは(斜体?)太字だったように思います.当時,これを手書きにするととても不細工になるので嫌いでした.電磁気か量子力学の参考書が普通の斜体に上に 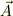 見たいで,その矢印が
見たいで,その矢印が  だったような気がします.うろ覚えですが,ファインマンさんの量子力学だったかもしれません.他方,砂田さんの理論電磁気学は
だったような気がします.うろ覚えですが,ファインマンさんの量子力学だったかもしれません.他方,砂田さんの理論電磁気学は 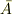 だったかもしれません.当時の版の本を見たいものです.
だったかもしれません.当時の版の本を見たいものです.
いずれにしろ,当時は矢印か横棒で手書きしたと思います.他方,当時,線形連立方程式のマトリックスを「太い立体の大文字」 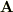 で,や1列ベクトルを「太い立体の小文字」
で,や1列ベクトルを「太い立体の小文字」 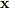 で表現し,行列式はマトリックスを2本の縦棒で挟んで,
で表現し,行列式はマトリックスを2本の縦棒で挟んで, 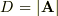 としていたと思います.
としていたと思います.
そこで,太いベクトルを見ると,マトリックスや列ベクトルを連想してしまい,とても不思議に見えてしまいます.ある種の浦島太郎・現象かもしれません.
>あと,cos, sin の引数に括弧がついているのが気になりました. >1つの項しかない場合は省略するのが一般的です. >cosh なども同様です.
これに付いては,考えるところと,感じるところがありすぎるので,すこし考えさせてください.
一応,フォーマルには,物理は数学と違って,すぐにプログラムすることも考慮して,リダンダントでも,見やすくするのが善い,と考えるからです.
本音は,記憶力が悪いので,三角関数の公式を覚えきれないので,それらを嫌悪しているので,引数が一つの場合,括弧を省略する特権を付与したくないのです.
逆に指数関数の場合,引数が一つの場合,括弧を省略する特権を付与しています.非論理的,恣意的なことですね.それゆえ,しばし考えさせてくださいまし.
>2階微分のところのダッシュが足りません.
さっそく訂正させて戴きました.有難うございました.
Re: 手に馴染むLaTeXe #01
mNeji さんのレス (2006/09/04(Mon) 22:29)
以前,この掲示板で作成した「LaTeXテンプレート」はある長さを越えることが出来ない上,長ければTeX変換のサーバに負荷がかかる可能性がありました.
今回,かぎしっぽのフォーマットにして,下記に査読の原稿として提出しました.これをご覧の上,ご意見があれば,是非ともお聞かせください.忌憚ないご意見をお願い申し上げます.
記事/LaTeX表現集(mNeji著) - 物理のかぎプロジェクトWiki
Re: 手に馴染むLaTeXe #01
mNeji さんのレス (2006/09/12(Tue) 02:21)
MXKさん:
以前のご意見で, >あと,cos, sin の引数に括弧がついているのが気になりました. >1つの項しかない場合は省略するのが一般的です. >cosh なども同様です.
これについて,私見を述べさせていただきます.
結論としては,この掲示版を含み,カジュアルな環境でアイデアを速記するという場面で式を書き出す場合は,系統的に括弧をつけるほうが間違いが少ないと思います.
#これに反して,筆記の場合, 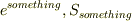 の場合,
#極力,括弧を省略しています.
の場合,
#極力,括弧を省略しています.
勿論,格式のある論文や書籍の原稿作成においては,その提出先のルールに従うべきと思います.
実際に数学系の図書にあたって見ると,特にマトリックス表現では,引数が1つの場合でも,明示的に括弧を付与するケースが多々あります.
勿論,公式集では,「引数が1つの場合」には括弧を付与しないルールが徹底しているように見受けられました.
以上が,自分の場合のクライテリアにしようと考えて居ります.論議を忘れないうちにご報告いたします.
Re: 手に馴染むLaTeXe #01
Chappy さんのレス (2006/09/12(Tue) 17:40)
数式を書くときには,意味が正確に伝わることが大事ですが,式の簡潔さも大事だと思います.
したがって, 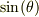 と表記するのは,
意味が正確に伝わりますが,簡潔さに欠けると思います.
また,
と表記するのは,
意味が正確に伝わりますが,簡潔さに欠けると思います.
また, 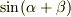 については,カッコをつけないと,
については,カッコをつけないと, 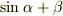 となり,
これは“
となり,
これは“ 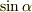 と
と 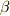 を足し合わせたもの”と,十中八九,そう解釈されるでしょう.
を足し合わせたもの”と,十中八九,そう解釈されるでしょう.
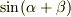 であると捉える人はまずいないと思います.
であると捉える人はまずいないと思います.
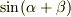 は,正確さ・簡潔さからこれ以上はないという表記だと思います.
は,正確さ・簡潔さからこれ以上はないという表記だと思います.
それとですね,「文脈で判断しろ」という数式の書き方もよくないと思います. それが書物だったら,大変ですね...読者を余計なことで迷わせてはいけませんよね.古い本ではたまにあるような気もしますが.それも誤植の一種でしょうか.
関係ない話ですが, 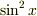 という書き方も,
という書き方も, 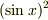 という書き方に比べ,式の簡潔さに一役買ってますね.
という書き方に比べ,式の簡潔さに一役買ってますね.
追伸:できるだけたくさんの本から,その本の内容だけでなく,数式の表記の仕方なども学ばなければなりませんね.逆に,多くの人の目に晒される,出版物等の責任は大きいです.まっとうな数式の表現に努めなければなりません.
Re: 手に馴染むLaTeXe #01
mNeji さんのレス (2006/09/12(Tue) 20:04)
「正確」・「簡潔」な記法と,そのツールを求めたのがTeXで,その入れ物自身をそのルールに似る様に努力したのがWikiではないかと感じます.
大昔の話です:
輪講の時に,計算ミスが発生して,辻褄があわなくなり,...,結果,Chappyさんが例示した 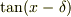 の
括弧を忘れ,さらに
の
括弧を忘れ,さらに  まで忘れていたのです.入力波が相互作用なしで出力波として出ただけでした(笑).
まで忘れていたのです.入力波が相互作用なしで出力波として出ただけでした(笑).
リダンダンシーとアキュラシーの論議で大騒ぎになりました.そのとき一人の人が「皆さん,傘を持って出るかどうかをどうやって決めますか?」と言い出しました.これはこれで,結構話が盛り上がりました.最後に,本人がぽつりと;
「だから毎日,鞄に傘をいれたままなのさ」
私は,それいらい,傘は鞄の中に入れっぱなしで,初等関数の括弧は付けっぱなしです.どう贔屓目に見ても, ・書く時に「括弧の入れる入れないを考える精神的緊張」, ・読むときに「括弧が無いのはミスでないかとテェックする手間」 よりも,単純に ・常に「括弧にいれて書く」方が良いと思います.
でも,これは個人の好き勝手な問題ですがね.
>「文脈で判断しろ」という数式の書き方もよくないと思います.
- 具体的に問題をお示しくださいますか.
> 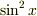 という書き方も,
という書き方も, 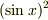
私の場合は,数式把握能力が低いので「正弦関数で,引数x,を自乗するのだな」と見れるので,後者を好みます.
確かに,簡潔性としては前者です.式の流れだけを追っている場合,私も前者がいいです.でも,一度,その式を使ってデータ分析するという場合,圧倒的に後者です.そのままプログラムに書けますから.
ああ,だから,簡潔性はそのテキストが使われる場面依存性によって支配されているのではないですか?
自分の感じでは,実験ノートとかアイデア・ノートは,迅速性と正確性が重要です.この掲示板もどちらかというとインフォーマルであると思います.
他方,査読記事などは,フォーマル仕立てなので,簡潔性が優先されるのですかね.
フォーマルな本や論文に,内容と同時に,簡潔さ,綺麗さに注意を注いでほしいと思います.
特に,
・文章と式のバランス, ・式への句読点, ・必要最小限の式番号とその配置,
については,コンピュータ・リテラシなどでノウハウを伝授するべきかもしれません.
私が「式の句読点」に気づいたのはファインマンさんの教科書だったような気がします.あの本は内容がチンプンカンプンなのに,一種のバランスの美みたいなタイプライティングと思いました.今一度,見てみたいものです.
Re: 手に馴染むLaTeXe #01
mNeji さんのレス (2006/09/12(Tue) 20:31)
追加の質問:
Q1 数学の図で,三角形ABCと文章でかき,図面で点ABC と記入しますが.この時の表現は立体ですか,斜体ですか?
Q2 数学の本で,「証明」の始りに白い□,終りに黒い■が付くようですが,この手の記号はほかにもあるのでしょうか?
Re: 手に馴染むLaTeXe #01
Chappy さんのレス (2006/09/12(Tue) 20:54)
初等関数の括弧は付けっぱなしは,個人の自由ですよね,失礼しました,,,.
>「文脈で判断しろ」という数式の書き方 具体例が出せません,,,ごめんなさい. 悪しき参考文献でもあればいいのですが,,,
Q1 三角形は立体が多いのですかねぇ.まぁ,あまり細かいことを気にする必要がないとは思いますよ.
Q2 人によってけっこう好みがあるようですね.mNejiさんのおっしゃるとおり,□もありますし,■も.筆記では□を荒く塗りつぶす方もいらっしゃるようです.他には,□に/を入れる方(“ます”です)もいらっしゃいますね.僕が見たことあるのはそれくらいですね.みんな四角ですが,○を書く人はいらっしゃらないのかな??
Re: 手に馴染むLaTeXe #01
toorisugari no Hiro さんのレス (2006/09/13(Wed) 15:00)
どちらにつけるか迷いましたが,本筋からは離れているのでこちらに書きます.
Re: ガウスの法則 mNeji
- 2006/09/12(Tue) 13:37 No.11869
において
> 例:ある曲面Sの法線方向 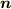 にむいた微小面積素
にむいた微小面積素 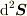 と電束密度との内積を曲面
と電束密度との内積を曲面  について加えたもの:
> 例:
について加えたもの:
> 例: 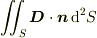
と書かれていますが,この 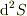 が気になります.私は上付き添え字の2に違和感を持つのですが,これがほかに使われている文献などをご存じでしょうか?
が気になります.私は上付き添え字の2に違和感を持つのですが,これがほかに使われている文献などをご存じでしょうか?
Re: 手に馴染むLaTeXe #01
mNeji さんのレス (2006/09/13(Wed) 17:40)
>この 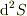 が気になります.
が気になります.
あっ,済みません.なんかの手拍子です.ご注意,有難うございました.
最近,砂川さんの「電磁気学の考え方」を入手しました.超久しぶりに 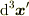 に接し,指が消すのを拒否したように推察されます(笑).
に接し,指が消すのを拒否したように推察されます(笑).
至急,訂正します.
Re: 手に馴染むLaTeXe #01
MXK さんのレス (2006/09/13(Wed) 20:07)
呼応して積分記号も1個でいいように思います. 面積分を重積分に直した時点で2つになるという考え方です.
Re: 手に馴染むLaTeXe #01
mNeji さんのレス (2006/09/13(Wed) 21:20)
添削,有難うございます.
>呼応して積分記号も1個でいいように思います. >面積分を重積分に直した時点で2つになるという考え方です.
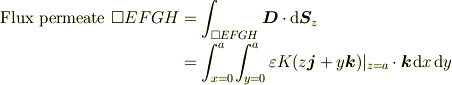
こういった意味でしょうか.「1つの面積分」=『「1つの線積分」と「1つの線積分」との直積』と言う感じでしょうか?
もし宜しければ,「□EFGHを通り抜ける電束」というのをなんて表現すれば良いのかご教示くださいますでしょうか? 思いついた単語をそのまま書いただけなので....
Re: 手に馴染むLaTeXe #01
toorisugari no Hiro さんのレス (2006/09/13(Wed) 22:21)
私は 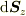 の
の  添え字もいらないかなと思います.
添え字もいらないかなと思います.
> 「□EFGHを通り抜ける電束」というのをなんて表現すれば良いのでしょうか?
英語の話ですか,日本語の話ですか,数式上の話ですか? わたしなら,式だけ
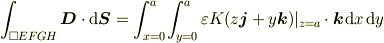
と書けば十分と思います.
>「1つの面積分」=『「1つの線積分」と「1つの線積分」との直積』と言う感じでしょうか?
上の式の左辺は座標系に依存しない表式,右辺は座標系に依存する表式なので,等しいといわれると抵抗があります.左辺を直角座標系で書き換えると『「1つの線積分」と「1つの線積分」との直積』になる,あるいは左辺の直角座標系での「表現」が直積になる,ぐらいでしょうか.
Re: 手に馴染むLaTeXe #01
mNeji さんのレス (2006/09/14(Thu) 01:47)
toorisugari no Hiroさん:
>z添え字もいらないかなと思います. >わたしなら,式だけ
なるほど,合点いたしました.有難うございます.
恐らく,MXKさんも,面倒なやつとお思いでしょうね(笑).
Re: 手に馴染むLaTeXe #01
toorisugari no Hiro さんのレス (2006/09/14(Thu) 09:52)
> 恐らく,MXKさんも,面倒なやつとお思いでしょうね(笑).
うーん,というよりmNejiさんのようにアクティブに書かれる方は貴重ですし(英語の話はかなり参考になりました),仮にそこに議論になるようなことがあったとしても,それはすべての人が参考になるものですから,これからもお互いに墓穴やらなにやら掘りまくりましょう.
Re: 手に馴染むLaTeXe #01
mNeji さんのレス (2006/09/14(Thu) 12:59)
toorisugari no Hiroさん:
>これからもお互いに墓穴やらなにやら掘りまくりましょう.
私の場合,天然ボケなので,自然に間違えまくってしまうような.
私の関係では,体積積分,線積分はちらほらあっても,面積分が先ず出てこないのに気づきました.何となく;積分の次数みたいな感じで,
・体積分,微小要素スカラー:次数3 ・面積分,微小要素ベクトル:次数2 ・線積分,微小要素ベクトル:次数1
見たいなイメージがあって,表現に混乱が生まれたみたいですね.
確かに,この手の思い込みは,使ってデバックしないかぎり判らないのかもしれません.
B3の夏休み直前に,正しい数式の書き方の練習をウェブ・サイトじょうでコンテスト形式でやって,相互評価させるような特別講義でもすると善いかもしれませんね.
Re: 手に馴染むLaTeXe #01
mNeji さんのレス (2006/09/30(Sat) 00:58)
このスレッドを立てた本人です.今日で,掲示板から卒業します.ついては,このスレッドでは返答いたしませんので,お許しください.
なお,LaTeX表現集に関しては,COさん,Chappyさんにバトンタッチさせていただいたので,宜しくお願い申し上げます.
ご指導ありがとうございました.