固体物理学で・・・
固体物理学で・・・
msndance さんの書込 (2006/08/18(Fri) 17:01)
キッテルの固体物理学入門で気になっているところがあります.
ひずみの成分exx=eyy=ezz=δ/3となる物体の一様膨張に対し,
U=C11/2(exx^2+eyy^2+ezz^2)+C44/2(eyz^2+ezx^2+exy^2)+C12(eyyezz+ezzexx+exxeyy)
C??:コンプライアンス定数
で表される立方結晶の弾性エネルギー密度Uは U=(C11+2C12)δ^2/6
体積弾性率Bを定義の-Vdp/dVに等価である U=Bδ^2/2 ※ で定義すると,立方結晶については B=(C11+2C12)/3
という説明に出会ったんですが,※の式とB=-Vdp/dVが等価であることを導くにはどうしたらいいんでしょうか.
Re: 固体物理学で・・・
篠原 さんのレス (2006/08/18(Fri) 23:24)
msndanceさん,はじめまして. 篠原です.
すみませんが,msndanceさんは大学生ですか? 学年,専攻などを教えていただけると助かります.
また,力学の基礎的な部分はもう習っておられますか? これをしっかり理解できているか否かで,説明の仕方が変わります... 以上,返答をお願いいたします.
(ちなみに,上式において係数 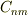 はコンプライアンス定数ではなく,スティフネス定数です...)
はコンプライアンス定数ではなく,スティフネス定数です...)
Re:+固体物理学で・・・
msndance さんのレス (2006/08/19(Sat) 09:55)
専攻は物理ではありませんが,力学,量子力学,弾性体力学,熱統計力学などを一通り独学してます.それらを前提とした説明にもついていけるかと思います.よろしくお願いします.
Re:+固体物理学で・・・
篠原 さんのレス (2006/08/19(Sat) 16:47)
> 力学,量子力学,弾性体力学,熱統計力学などを一通り独学してます.
おぉ・・・ すばらしい・・・・ 私の苦手とする分野ばかりを独学とは・・・
苦手ですので,私の考えが合っているかわかりませんが,感覚だけでも伝われば幸いです.
今,簡単のために簡単なバネの問題でのアナロジーを考えましょう.
ご存じの通り,バネの自然長から 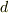 だけずれた位置にある質点がバネから受ける力は,
だけずれた位置にある質点がバネから受ける力は,
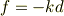
ですよね.
ここで,  となります.(Bの定義と似ていますよね.)
このとき,バネに蓄えられたエネルギーを考えると,
となります.(Bの定義と似ていますよね.)
このとき,バネに蓄えられたエネルギーを考えると,
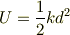
を導くことができますよね.
(仕事の定義より,物体にかかる力を平衡位置から 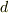 まで積分すると求められます.)
まで積分すると求められます.)
ここで, 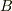 の定義をみてみると,バネ常数と同様の定義となっていますよね.
仮に
の定義をみてみると,バネ常数と同様の定義となっていますよね.
仮に 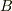 が一定であるとすると,その定義は,
が一定であるとすると,その定義は,
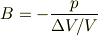
と書き直せますよね.
ここで,適当な立体を仮定して,それにかかる圧力を,体積の変化と 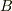 を用いて上式から求め,そこからエネルギー密度を求めると
を用いて上式から求め,そこからエネルギー密度を求めると 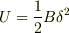 となります.
となります.
今は時間がないのでこの辺まで・・・. 一度ご自分で計算してみてください.
# 説明がわからなければ,お気軽にご質問ください.
Re:+固体物理学で・・・
msndance さんのレス (2006/08/20(Sun) 16:35)
すいません,頭がごちゃついてきました.
p=-BΔV/Vとf=-kdを比べると, 前者の式にはΔVが入ってますよね. あとは,x,y,zの3方向に力が加わっていることを考えればいいんですよね.
う〜〜ん,そこらへんがうまく計算できないです・・・.
Re:+固体物理学で・・・
篠原 さんのレス (2006/08/20(Sun) 19:30)
数式だけを眺めていても,問題はなかなか解けません. 具体的な問題を設定し,物理的イメージを持ちながら解くことをお勧めします.
あと,いきなり難しい問題を設定してもなかなか答えにたどり着けません. まずは簡単な問題を設定して問題を解いてみてください.
問題を簡単にするために,1方向だけから力が加わっている場合について考えましょう.
断面積 S の円柱を設定し,その長さを L とします.
円柱の軸方向に力がかかり,その長さが d だけ変化したときのエネルギー(密度)を求めてみてください.
ここで, 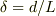 に注意すると,エネルギー(密度)の式が求まります.
に注意すると,エネルギー(密度)の式が求まります.
# 大学院入試前で,今はあまり時間が取れません. # 大変申し訳ありませんが,丁寧に導出を書いている時間は無いので,出来るだけ自力で解いてください. # もちろん,分からない点があれば,お気軽にご質問ください :)
Re:+固体物理学で・・・
mNeji さんのレス (2006/08/20(Sun) 21:56)
msndanceさん:
始めまして.私は,物性が苦手で,その手の本が手持ちにないのですが,体積弾性率というのは,考える対象を等方的に加圧していく時の体積の変化率を考えるわけですよね.理化学辞典で体積弾性率を見ると
いま圧力が, 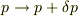 と変化する時に体積が
と変化する時に体積が 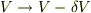 変わるときに,体積弾性率
変わるときに,体積弾性率  とすると
とすると
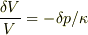
逆に
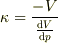
一方,資料が立方体なら
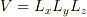
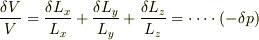
各方向ごとの歪は,圧力変化 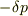 と歪テンサで表現できる筈ですね.外していたら,御免なさい.
と歪テンサで表現できる筈ですね.外していたら,御免なさい.
Re:+固体物理学で・・・
msndance さんのレス (2006/08/20(Sun) 22:36)
mNejiさん,篠原さん>
すみません,ちょっと勘違いしてたようです.立方結晶に限らず,もっと一般的な話だったように思います.もっとテキストの本文を熟読すべきでした.
δ=dV/V≒exx+eyy+ezz という膨張に関する式を忘れていました.
dp=-BdV/V=-Bδ この圧力に逆らって単位面積あたりBδの力を加えて膨張させていくので ばねの弾性エネルギーと同様に積分すれば U=(1/2)Bδ^2になる・・・でよかったですかね. 単位面積あたりの力である圧力を積分した結果ですので, 弾性エネルギー密度の「密度」というのは,単位面積あたり・・・という意味でよろしいでしょうか?>篠原さん(入試勉強忙しい中すみません,お時間のあるときで結構です)
Re:+固体物理学で・・・
篠原 さんのレス (2006/08/20(Sun) 23:12)
mNejiさん,こんばんは. フォローありがとうございます. 助かります.
msndanceさん,そのとおりです. 問題を設定しなくても解けるとは・・・ 頭の回転が速いですね.
一見,無次元量  による積分に見えますが,その本質は仕事の定義である 力を距離で積分していることに注意してください.
による積分に見えますが,その本質は仕事の定義である 力を距離で積分していることに注意してください.
エネルギー密度ですが,これは面積あたりではなく,体積あたりと言う意味です. 単位に注意しながら式を追いかけてみてください.
Re:+固体物理学で・・・
msndance さんのレス (2006/08/20(Sun) 23:33)
あ,そうですね,変位方向に関する微小距離をかけないと仕事にならないですからね.
えーっと,エネルギー=N・m エネルギー/体積=N/m^2
[B]=[-Vdp/dV]=[p]=N/m^2
あ・・・確かに・・・.圧力の次元と単位体積あたりのエネルギーは同じなわけですね.
とんだ独断に陥るところでした.私はまだまだですね.
熱的振動
msndance さんのレス (2006/09/06(Wed) 15:14)
あれからキッテルの固体物理学を読みすすめ,フォノンの熱的振動のところまできました.
それで,フォノンII:熱的性質の問題2なんですが・・ 300Kナトリウム格子定数a=4.225*10^{-8}cm の基本単位格子の 熱膨張率ΔV/Vの2乗平均を求める.体積弾性率は7*10^{10}erg・cm^{-3}
解説を読んでいましたところ,
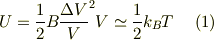
ナトリウムは体心立方格子基本格子の体積Vは
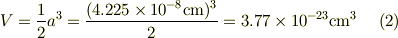
これらの数値を代入して,
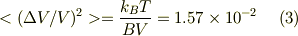
ΔVがマクスウェル分布をとっている場合
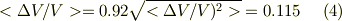
?.(1)式の真ん中の辺で(ΔV/V)^2の右側にVがついていて,どうして?と思いました.No.11415ではB=(1/2)B(ΔV/V)^2 δ=ΔV/Vとなっていたからです. ?.また,右辺の1/2というのはどこから出るのかと思いました. ?.(4)の真ん中の式なんですが,0.92という数値はどこから出てくるのでしょう.
キッテルの本の本文を読んでも理由が思い浮かばなくて困っております. 問題の解説のほうは,「キッテル固体物理学演習」をみております.
Re: 熱的振動
toorisugari no Hiro さんのレス (2006/09/06(Wed) 16:38)
詳しい方がfollowしてくださるまでのつなぎとして.
- 片方がエネルギー密度,もう片方がエネルギー.
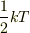 は1自由度のエネルギー(等分配則を調べてください.)
は1自由度のエネルギー(等分配則を調べてください.)- 手元に資料がないのでわからないですが,平均を定義するときに出てくる(数学的な)定数だと思います.
Re: 熱的振動
msndance さんのレス (2006/09/06(Wed) 17:12)
ありがとうございます.(1)(2)まで理解しました.
Re: 熱的振動
toorisugari no Hiro さんのレス (2006/09/06(Wed) 21:45)
(3)
 がMaxwell-Boltzmann分布
に従うとき,絶対値の平均とR.M.S(2乗平均の2乗根)は
がMaxwell-Boltzmann分布
に従うとき,絶対値の平均とR.M.S(2乗平均の2乗根)は
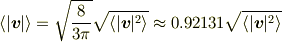
の関係を満たします.
きちんと計算をしめしたURLは見つからなかったですが,とりあえず,
# でも体積がMB分布???何か変.
Re: 熱的振動
msndance さんのレス (2006/09/07(Thu) 13:13)
う〜ん,熱統計の本を見返してみましたが,MB分布は速度に関するものですよね.
体積と速度の関係がはっきりすれば,ΔVもMB分布に従うかどうかはっきりするのですが・・・.
Re: 熱的振動
mNeji さんのレス (2006/09/07(Thu) 14:47)
門外漢ですが,各格子間の相互作用が「長距離」であれば,格子の熱振動子が相互にエネルギー伝達するような意味で「速度の分布則」を「エネルギーの分布則」に置き換える強引近似もありえるのかな?,と感じます.
そういわれると,アインシュタインさんの誘導放射の話も,とてもラフな論議(光を一つの調和振動子とする!)といった中から生まれたように思います.
と言いつつ,振動方向は3自由度あるのに,エネルギの等配分が
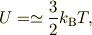
にならないのが判らない?,ですね.
Re: 熱的振動
msndance さんのレス (2006/09/08(Fri) 08:45)
は,おそらく1/2kBTの定数倍程度のオーダーである,という意味あいなんだと思います.
問題の解説では1/2kBTを使った記述はないので,あまりこだわらなくてもいいのかもしれません.
MBのほうはもうちょっと考えてみます.