教えてください><
教えてください><
よーこ さんの書込 (2006/08/17(Thu) 11:13)
1日考えましたが無理でした・・. 問) http://chance.moo.jp/denji2.PNG 図のような同心球導体1,2,3があるとき,各導体の電位V1,V2,V3を以下の各問いの条件時に求めよ.
a)導体1,3にそれぞれQ[c],−Q[c]を与えたときにV1,V2,V3を求めよ.
b)導体1,3にそれぞれQ[c],−Q[c]を与えた上で導体2と3を細い導線で接続したときのV1,V2,V3を求めよ.
c)導体1,3にそれぞれQ[c],−Q[c]を与えた上で導体1と3を細い導線で接続したときのV1,V2,V3を求めよ.
Re: 教えてください><
mNeji さんのレス (2006/08/17(Thu) 18:02)
とりあえず,考えるヒントを示してみます.
静電気の性質は,重力の性質と良く似ています.例えば,示された図で言えば,導体3に-Q(C)の電荷がある時の電場と,導体3の重量がM(kg)ある時の重力(場)は共に逆自乗の法則に従います.今,同心球の原点に座標原点が一致しているとして,
いま, 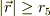 の場合を考えると;
の場合を考えると;
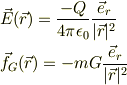
となり,それぞれ原点に点電荷-Qが,点質量Mがある場合の逆自乗の公式に従いますます.ところが, 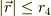 の場合を考えると;
の場合を考えると;
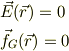
と一転して場が消滅します.まさにマジックです.
これを,もう少し詳しく言えば,球面上に分布した電荷や質量の分布は,あたかも原点に位置する点の作る場と同じ場を作るので,そのポテンシャル・エネルギーも当然,点が作り出すポテンシャルと同様に 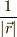 に比例します.ところが,一度,その分布の内側に入ると,場が消滅する,力が働かない為に,ポテンシャル・エネルギーは一定になってしまうのです.
に比例します.ところが,一度,その分布の内側に入ると,場が消滅する,力が働かない為に,ポテンシャル・エネルギーは一定になってしまうのです.
Re: 教えてください><
篠原 さんのレス (2006/08/17(Thu) 20:47)
よーこさんはじめまして. mNejiさんこんばんは. 篠原です.
> よーこさん,
Yahooの掲示板でも全く同じ質問をされていますね. 当掲示板でマルチポストは禁止されています. 気をつけてください.
また,「無理でした」では,こちらはあなたが何が分からないのか分かりません. 大学生なら,もう少し大学生らしい質問の仕方があるでしょう・・・.
Re: 教えてください>< ←解説ノート
mNeji さんのレス (2006/08/20(Sun) 10:59)
■■ 球面上に分布する静電場を考えるノート ■■ by mNeji at 2006-08-19 ■■
この問題は,静電荷の球面分布に関する典型例なので,ステップ・バイ・ステップで思い出しながら解説を書き出してみます.と言って,新しい事は何も出てくるわけでありません,念の為に.説明は,よーこさんのオリジナル図に従って書いてあります. http://chance.moo.jp/denji2.PNG
スレッドを立てられたよーこさんのオリジナルの質問に付いては,下記サイトが詳しい説明をされているようです;
◎ 電磁気(今澤良太さん) - http://csx.jp/~imakov/elemag/elemag.html
私が下手な説明をするより,こちらをご覧になることをお勧めします.
でも,これらの解説をご覧になっても<b>釈然としない方</b>もいらっしゃると思います.かく言う私も,静電荷の計算問題,特に「アース」が入った問題は胡散臭くて大嫌いでした.今回の問題は,「アース」の話が無いので,持論を整理して説明ノートにまとめたいと思います.
さて,問題の静電場を求める事が判り難い原因は,静電荷の方程式(微分形式→積分形式)を誘導してくるまでに;
○微分形:単位体積中の電荷に比例して,電場の発散が生じる.
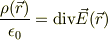
| | なが〜い数学の旅が続く! ので,重要な仮定が消えてしまったりする!?! ↓ ○積分形:詳しい説明は→「■4■ 静電場の方程式」にある.
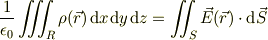
| ↓ ○実際の計算に向かう時に, ・必要な条件や考え方は何? ・積分形の方程式をどう処理するのか?
ズバリ,それを指摘すると;
■1■ 金属の電気的性質と電場の関係 ■2■ ガウスの定理(ヴェクタの発散の体積積分=ヴェクタの面積分)の解釈 ■3■ ヴェクタの面積分が解ける条件
だと思います.では大雑把に,これらをレビューしましょう.
――――――――
■1■ 金属の電気的性質と電場の関係
此処では,金属を単純に近似します:
・金属中には自由電子が一杯いて,外部から電場がしようとすると,逆の電場をすぐ作る.従って,金属内部には電場は存在しないし,電流も流れない. ・金属表面では,外部電場は表面に垂直成分しか持たない.もし,表面に平行な成分の電場ができれば,上に述べた自由電子によって,すぐキャンセルされるからだ. ・金属に外部電荷を注入すると,外部電荷同士相互に反発し,金属表面になるべく離れて分布する.この時の電荷分布が平衡する時間は非常に早い,事実上,瞬間に平衡すると近似する.簡単なはなし,形状が尖った部分に電荷が移動し易い. ・簡単な話,金属は理想的な電荷のコンテナであると考える.そして,電荷は常に外側にむかって分布する.
■2■ ガウスの定理(ヴェクタの発散の体積積分=ヴェクタの面積分)の解釈
・考える領域を「ゴミ袋」で滑らかに包むことをかんがえる.この袋全体の外向きの面を厳かに面「 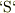 」と命名する.→ 電場ヴェクタの面積分
・この袋の内部の体積部分を厳かに領域「
」と命名する.→ 電場ヴェクタの面積分
・この袋の内部の体積部分を厳かに領域「 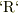 」と命名する.
→ 電荷密度の体積分=含まれる金属に注入されている外部電荷(真電荷).
→ 金属相互の誘導電荷は関係ない!(アースが無い限り)
→ 金属同志が「入れ子」になっていようが,「別々」になっていようが関係ない.
」と命名する.
→ 電荷密度の体積分=含まれる金属に注入されている外部電荷(真電荷).
→ 金属相互の誘導電荷は関係ない!(アースが無い限り)
→ 金属同志が「入れ子」になっていようが,「別々」になっていようが関係ない.
■3■ ヴェクタの面積分が解ける条件
電荷分布から直接的に電場分布を出すには,もう少し微分方程式の解法を勉強する必要があります.でも,その結果だけなら皆さんも良くご存知のクーロンの法則を適応して出してしまえばいいだけです.といっても,腕力がいるので,色々なテクニックを必要とします.
此処では,面 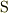 を通して出て行く電場の面積分が判り易く解ける条件を3つ説明します.
を通して出て行く電場の面積分が判り易く解ける条件を3つ説明します.
・平行電極(コンデンサ)のような場合:
→ 電極の端を無視するために,無限大の面を仮定する.
・同心筒のような場合:
→ 電極の端を無視するために,無限大の長さを仮定する.
・同心球のような場合:
→ 端がなく,球対象だから,中心方向の成分だけ: 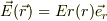
今回の説明は,最後の条件を考える事ですね.
■4■ 静電場の方程式
●真空中での静電荷が作り出す電場の方程式:微分形と積分形
○微分形:単位体積中の電荷に比例して,電場の発散が生じる. 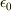 は真空の誘電率である.
は真空の誘電率である.
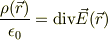
○積分形:「領域Rに含まれる真電荷の総和」は「領域Rの表面Sを内側から外にむけてでる電場の面積分」に比例する.
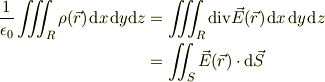
ここで
・  の一部の微小面積を
の一部の微小面積を 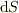 とし,
その部分の内側から外に向いた法線ヴェクタを
とし,
その部分の内側から外に向いた法線ヴェクタを 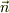 とすると,
・微小面積ヴェクタは
とすると,
・微小面積ヴェクタは 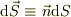 となる.
となる.
上式の右辺で,体積分から面積分への変形には「ガウスの定理」を用いている.
◇◇◇ コーヒー・ブレイク#0: ガウスの定理のガウスさんって?◇◇◇◇◇◇
ちなみに,理化学辞典第3版によると; ガウス [英 Gauss, Carl Friedrich] 1777-1855. ドイツの数学者. 途中略.青年時代に整数論を熱愛し,...1812年に超幾何級数を論じ, 1827年には曲面論を展開するなど,代数学,解析,幾何学などの各方面に 大きな貢献をした. また,1800-20年の間は主として天文学に,1820-30年は測地学に, 1830-40年は物理学とくに<b>電磁気学</b>に,それぞれ著しい寄与をした....
#わが国でいえば江戸時代の後期に,この様な研究をされていたかと思えば.... #電磁気を53〜63歳にかけて研究したんだ,ヒェー. #ベクトル解析も,PCも無い時代だからこそ出来たのだろうが,感謝.
◇◇◇◇◇◇◇◇◇ ガウスさんの言葉: Chappyさんのページから抜粋 ◇◇◇◇◇◇◇◇◇
pauca sed matura (狭くとも深く)−Carl Friedrich Gauss−
◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇
■5■ 具体的な計算
◆5.1◆ 導体3にだけ電荷がある場合.
示された図で言えば,導体3にQ_3(C)の電荷がある時の電場を求める.同心球の原点に座標原点が一致するようにとる.
半径  の球面を
の球面を  に取ると,領域
に取ると,領域  は半径
は半径 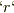 `の球体全部.
半径rでの電場,
`の球体全部.
半径rでの電場, 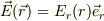 半径rでの微小面積ヴェクタ,
半径rでの微小面積ヴェクタ, 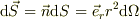
従って
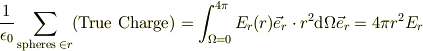
故に
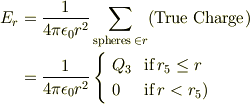
この様に,金属球面に真電荷が均一に分布した場合に,その金属球面より外側に出来る電場は,その中心に点電荷として存在した場合のクーロンの法則に一致する.
ところが,その金属球面より少しでも内側にはいると,電場は完全に消滅する.言い換えると,球面上に分布した均一電荷はその内側に電気力線を延ばせないのだ.
この現象は,静電場が電荷からの距離の逆自乗の法則(クーロンの法則)に従うことによる.事実,クーロンの法則に従って,電場の直接積分しても,球内では電場が零となることが確かめられる.
◇◇◇ コーヒー・ブレイク#1: クーロンの法則を直接に積分◇◇◇◇◇◇
B1でこの話を知ったときに,にわかに信じられなくで,球面に均一電荷分布を考えて,クーロンの法則から球内部の電場を直接に積分したことがあります.部分積分を幾つか重ね,一見キャンセルしなさそうな積分が一気に消滅したのを見て,電荷の体積分の効能を実感した記憶があります.
万有引力もクーロンの法則に従うので,まったく同じことがいえます.従って,静電場が相対論的な拡張に従うのと類似の形式で,重力場(万有引力)も相対論的な拡張をすることが出来るようです.面白いですね.
◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇
◆5.2◆ 導体3と導体2に逆符号の電荷がある場合.
恐らく,この段階に来て,静電場の醍醐味を味わうことが出来ると思います.味噌は,静電誘導です.
導体3に電荷 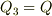 ,導体2に電荷
,導体2に電荷 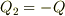 ,導体1に電荷
,導体1に電荷 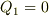 であることを考えます.
であることを考えます.
- 半径
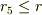 の領域を考えると
の領域を考えると
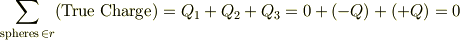
なので, 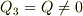 にも関わらず,外側に電場が存在しません.
にも関わらず,外側に電場が存在しません.
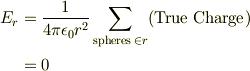
- 半径
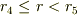 の領域を考えると
の領域を考えると 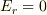
この領域は,導体3の内部であるので,電場は零; 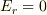 .
.
- 半径
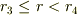 の領域を考えると
の領域を考えると
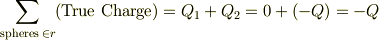
従って,この領域では,
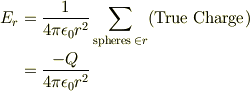
- 半径
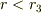 の領域を考えると
の領域を考えると
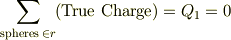
従って,この領域では,(i)と同様に,
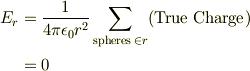
以上が,積分系の静電場の方程式の解を整理した結果です.でも,それだけでは何か論議が不足していませんか? よく見ると,電場は導体2と導体3の間にしか存在しませんし,そこに蓄積されている電荷は(-Q:+Q)です.そう,まさ導体2と導体3はコンデンサと同様の振る舞いをしているのです.
<pre> <図1断面図のイメージ:正確な絵ではない>
⇒ 球の外側 ⇒
電場 電場=ゼロ |←←←←←←←| ↑ ┌―――――┐┌―――――――┐| |導体2||導体3|| |||||
真電荷 -Q 真電荷 0 真電荷 +Q _電荷同志キャンセル 誘導電荷 0 誘導電荷 +Q 誘導電荷 -Q / 実効電荷 -Q 実効電荷 +Q 実効電荷 0
</pre>
積分系の方程式の計算では,あくまで「真電荷」で計算します.でも,実際の電場の出来方を把握するには,真電荷に誘導電荷を加えた; ・実効電荷=真電荷+誘導電荷 で考える方が直裁であることが判ります.
なお,注意したいのは,内側の導体から外側の導体に電場が繋がっている場合です.外側の導体の電荷はいくらあっても,内部へ影響しないので内側の電極に静電誘導を起こしません.
#見方を変えると,内側の真電荷から生じた電場は,外側の電極の内側に静電誘導を起こして初めて着地できる訳だ!
他方,真電荷が料理用ラップのような絶縁フィルムの表面にスプレーされているような場合,静電誘導を起こさないので,導体2,3からの電場はそれぞれ独立に出て行く.
<pre> <図2断面図のイメージ:正確な絵ではない>
⇒ 球の外側 ⇒
電場|→→→→ __電場同志でキャンセル |←←←←←←←←|←←←← / |
┌┐┌┐|
フィルム2||||フィルム3↓ ||||電場=ゼロ
真電荷 -Q 真電荷 +Q
</pre>
◇◇◇ コーヒー・ブレイク#2:静電誘導を力学と比較する ◇◇◇◇◇◇◇◇◇ 力学との類推をします.
運動方程式はあくまで,静止系ないしは定速度で動く慣性系で立てますね.一度,慣性系で全ての力を書き入れて運動方程式が出来上がれば,あとは計算しやすい適切な非慣性系に変換して解けばよかった訳です. <pre> ●力学●静電気学 慣性系での運動方程式微分系形・積分形の静電方程式/クーロンの式 全ての「外力」系に含まれる全ての「真電荷」 || ↓↓ 非慣性系:見かけの力金属での静電誘導 / /
↓ 直感的に判り易いが,間違いもしやすいので注意!
</pre> ◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇
此処まで来て,静電荷の問題はかなり身に付いたはずです.
時間がとれたら,電位とかアースについても考えて見ましょう.(2006-08-20)