レインマン さんの書込 (2006/08/16(Wed) 22:24)

大学受験生のレインマンと申します．わからない問題があったので 質問します

二枚の金属板が真空中で だけ隔てて平行に配置されている． 図１のようにこれらの金属板には起電力 の電池が接続されている． 金属板の面積は十分に大きく，この回路における電気抵抗や 電池の内部抵抗は無視でき，始め金属板と回路の電荷の総和は0であるとする． 極板間に負電荷-ｑ[c]，質量 の粒子があるとき もともと蓄えられていた電荷のほかに，静電誘導により， それぞれの極板の向かい合った面上に電荷が誘起される． 各極板に誘起された電荷の大きさを求めるのは簡単ではないが ，個々では単純に飛行中の粒子の負の極板からの距離を とし，定数 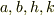を用いて，

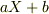（正の極板に誘起された電荷）＝ ? （負の極板に誘起された電荷）＝ ?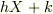

の関数形になると仮定する．但し，極板に誘起された電荷とは 粒子を置くことにより極板の向かい合った面に誘起された電荷とする． また，粒子の大きさは無視できるので， 粒子をおくことにより，コンデンサーの容量は変化しないものとする． （イ）Ｘ→0とＸ→ｄの極限で正負の極板の向かい合った面に誘起される 電荷を求め，?，?式中のa,b,h,kを求めよ

この問題でＸ→0の時負の極板に+ｑ誘起されるので +ｑが正の極板から来たと考えたのですが 答えを見ると 正の極板0 負の極板ｑ となっていました 説明を見ても良く分かりません 返答していただけたらうれしいです出典は関西学院大学改らしいです

mNeji さんのレス (2006/08/17(Thu) 01:55)

始めまして：

なにか仰々しい割りに，「この回路における電気抵抗や電池の内部抵抗は無視でき」と

（正の極板に誘起された電荷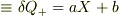） （負の極板に誘起された電荷）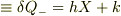

とすると，

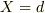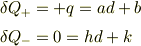
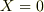の時

の時

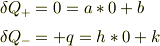
以上の4式から，パラメータを求めるのでは？

ｙama さんのレス (2006/08/17(Thu) 10:38)

レインマンさんは，誘起された電荷は正の極版から来ているのだから，正の極版の電荷も変化するはずだと考えられたわけですね．確かに，回路がどこにもつながっていなければ，全体の電荷が保存されるので，そういうことになりそうです． しかし，図１がどうなっているのか分かりませんが，回路のどこかが接地されているのではないでしょうか．接地されていれば，地面との間で電荷のやりとりができるので，全体の電荷も変化することができます．

レインマン さんのレス (2006/08/17(Thu) 22:08)

mNejiさんｙamaさんお返事ありがとうございます． 図１はコンデンサーに電池が繋がれているだけの回路で 接地されていません 私は電気容量とコンデンサーにかかる電圧が一定なので コンデンサー内の電荷はQ=CVで一定と考え 負極板にｑの電荷が来るなら正極板に-ｑの電荷が現れると思ったのですが， 解説によると最初系全体は中性であるので-qの電荷を極板間におくと 両極板に-ｑ/2の電荷が現れ，X→0のときは -q/2[c] ↑ +Q[c] d ●-ｑ[c] ↓_____________________ -Q[c]+q -q/2[c] 正の極板に誘起された電荷＝0[c] 負の極板に誘起された電荷＝q[q] となっていました． -qの電荷を極板間におくと両極板に-ｑ/2の電荷が現れるの はどうしてなんでしょうか また極板の電荷の和が答えと合っていないのではないでしょか． 絵が分かりにくくてすみません．

mNeji さんのレス (2006/08/17(Thu) 23:24)

レインマンさん：

読めば読むほど判らなくなってしまうのですが．

出来れば，レインマンさんの意見は入れずに，問題を完全に示していただけませんか？

レインマン さんのレス (2006/08/18(Fri) 21:07)

二枚の金属板が真空中でｄ[m]だけ隔てて平行にに配置されているれている． 図１のようにこれらの金属板には起電力の電池が接続されている． 金属板の面積は十分に大きく，この回路における電気抵抗や 電池の内部抵抗は無視でき，始め金属板と回路の電荷の総和は0であるとする．

(1)時刻ｔ＝0に負の極板の上に負電荷-ｑ[c]質量ｍ[kg] の粒子をおいた．粒子は金属板間の電場により加速されて正の極板に衝突し 静止する．粒子の加速度が0の場合衝突した時刻と衝突直前の粒子の速さおよび運動エネルギーはいくらになるか．ｑの大きさはあらかじめ極板に充電されている電気量に比べて非常に小さいが，電子１個のもつ電荷の大きさに比べれば十分に大きいとする．なお，粒子の大きさは無視し，重力の影響も無視してよい．(1)(2)（イ）

(2)粒子が極板間にあるときもともと蓄えられていた電荷のほかに， 静電誘導により，それぞれの極板の向かい合った面上に電荷が誘起される． 各極板に誘起された電荷の大きさを求めるのは簡単ではないが ，個々では単純に飛行中の粒子の負の極板からの距離をXとし とし，定数abhkを用いて，

（正の極板に誘起された電荷）＝aX+b ? （負の極板に誘起された電荷）＝hX+k?

の関数形になると仮定する．但し，極板に誘起された電荷とは 粒子を置くことにより極板の向かい合った面に誘起された電荷とする． また，粒子の大きさは無視できるので， 粒子をおくことにより，コンデンサーの容量は変化しないものとする． （イ）Ｘ→0とＸ→ｄの極限で正負の極板の向かい合った面に誘起される 電荷を求め，?，?式中のa,b,h,kを求めよ (ロ)粒子が正極版に衝突する時刻をｔ＝ｔ0（ティーゼロ） とするときｔ＝0からｔ＝ｔ0（ティーゼロ）までの間回路に流れる電流の大きさを時刻ｔの関数として求め，グラフに描け （ハ）時刻ｔ＝0からｔ＝ｔ0（ティーゼロ）までの間電池のした仕事はいくらかまたこの仕事はどのようになったか簡潔に説明せよ

高校過程の範囲内なのか疑いたくなるような問題ですが 問題集に出てきて困っています 質問点を明確にすると 最初系全体は中性であるので-qの電荷を極板間におくと系が帯電して 両極板に-ｑ/2の電荷が現れるのはなぜか

＞＞ 答え

(2)（イ） X=0の時 （正の極板に誘起された電荷）＝0 （負の極板に誘起された電荷）＝ｑ X=ｄの時 （正の極板に誘起された電荷）＝ｑ （負の極板に誘起された電荷）＝0 （ロ）I＝ｑ＾2Vｔ/md^2 (ハ）W＝ｑｖ 粒子の運動エネルギーになり，粒子が極板に非弾性衝突して に熱エネルギーにかわった

mNejiさん 答えの導出過程も教えてくれるとありがたいです

図1も書こうと思いましたが無理でした．前述したとおり コンデンサーに電池が繋がれただけの回路でアースされてないです

mNeji さんのレス (2006/08/18(Fri) 22:43)

大変申し訳ありませんが，この問題は高校生さんが入試の為に勉強するべきものとは思われません．従って，正式に回答することをお断りします．ただその理由を下記に示します．

【理由1】

《(1)時刻ｔ＝0に負の極板の上に負電荷-ｑ[c]質量ｍ[kg]の粒子をおいた．》に対して：

a) この粒子と極板との電気伝導の説明が無い． b）この粒子の運動の初期条件が明示されていない． c）「c」という単位は存在しない．電気量の単位は「C」である． d）電極間の電位差が明示されていない．なお電位の単位は「V」である．

【理由2】

《(2)粒子が極板間にあるときもともと蓄えられていた電荷のほかに， 静電誘導により，それぞれの極板の向かい合った面上に電荷が誘起される．》に対して：

静電誘導を考えるなら, 粒子運動を考えるときに，すでに考慮するべきとおもう．確かに，その効果は摂動として考えるという論理も有ると思うが，そんな考え方ができるのは，大学生でも高学年でないと無理ではなかろうか？

そのうえ，誘導電荷の仮定が不自然とおもう．

以上，私の理解するところです．出題された方にこの意見をご覧戴いて，ご意見を頂ければ，幸いです．

レインマン さんのレス (2006/08/18(Fri) 23:15)

c）「c」という単位は存在しない．電気量の単位は「C」である． d）電極間の電位差が明示されていない．なお電位の単位は「V」である． 写し間違えました．すみません 原典を改題してあるのでおかしくなってしまったのでしょうか? 原典を見たことが無いので分かりませんが. 某予備校の問題集で結構気に入っているので この問題だけ飛ばして進もうかと思います． 皆さん返答ありがとうございました

yama さんのレス (2006/08/18(Fri) 23:36)

問題の不備な点は，できるだけ辻褄が合うように解釈するとしても，その解答が正しければ全体の電気量が変化することになりますが，これはおかしいですね． ひょっとすると原典の図を正確に写していないのではないか，つまり，原典の図ではどこかが接地されているのではないかというような気がするのですが・・・．

mNeji さんのレス (2006/08/18(Fri) 23:52)

レインマンさん：

>この問題だけ飛ばして進もうかと思います．

賢明な結論と思います．現実に，受験時にも「間違い問題」が発生しているので，受験側も万一に備えて，「問題を逆観察して，時間を無駄に使わない」練習と思ってください(笑)．

ベストを尽くされますように．

MXK さんのレス (2006/08/19(Sat) 12:06)

レインマンさん，

解答は合っていると思います．

(正電極に誘起される電荷)＋(負電極に誘起される電荷) = q

が, 電荷 (-q) の位置 X に拘わらず成り立ちます．中性条件から，別に -q の電荷がどこかになければいけませんが，これは電極間に置かれた電荷から「一番遠いところ」，つまり電池の付近に押しやられています．

yama さんのレス (2006/08/19(Sat) 18:43)

なるほど，導線や電池の電気容量が十分大きければ，それを地球と同様に見なして電荷をやりとりさせることができますね． しかし，電池や導線の電気容量は極板の電気容量に比べるとかなり小さいので，そう見なしていいかどうかは疑問です． それはともかくとしても，このような電気回路の問題では，特に断りのないかぎり，導線や電池の電気容量は0であると理想化して考えるのが普通だと思います． 今回の問題では，その理想化が成り立たないとしても，高校生にそこまで考えさせるのは無理があるように思います． この種の問題では，どこかで接地するように設定するのが普通だと思います． 接地なしで，導線や電池の電気容量についての断り書きもないような今回の問題は，高校生対象の問題としては不備であると思います．

MXK さんのレス (2006/08/19(Sat) 19:52)

接地がないから不備だということはないと思います．

系全体を接地されていない1つの導体と考え，そこに電荷(-q)を近づけた状況と考えればいいでしょう．電荷に近いところ（両電極の内側）に全体として (+q)が誘起され，最も遠い側に (-q) が追いやられるということです．

箔検電器を想像してみてください．電池が気になるのなら，とりあえず起電力を0とする,すなわち電線で置き換えた場合を考えればよいと思います．

もし回路が全く接続されておらず，電荷(-q)がちょうど中央にある場合には，(-q/2)の電荷がそれぞれの電極の外側に追いやられることになります．電極ごとに中性条件が満たされているということです．

yama さんのレス (2006/08/19(Sat) 21:08)

導線や電池の電気容量が0ならば，そこに電荷を追いやることはできなせん． 高校物理では，普通は導線や電池の電気容量は0と考えると思います． 高校物理の問題集でも，導線の抵抗や電池の内部抵抗を考慮する問題はありますが，電気容量を考慮する問題はほとんど皆無だと思います． 箔検電器の場合は，箔自体がある程度の電気容量をもっていることは高校生でも考えられるでしょうが，導線や電池に電気容量があることを，高校生に考えさせるのは無理があるのではないでしょうか．

>もし回路が全く接続されておらず，電荷(-q)がちょうど中央にある場合には，(-q/2)の電荷がそれぞれの電極の外側に追いやられることになります．電極ごとに中性条件が満たされているということです．

極板が十分広くて端のほうの電荷分布を考えないなら，そのようになりそうです．この場合，内側の電荷分布は，両極板が接地されている場合と同じですね． しかし，電荷が中央からずれた場合は，内側の電荷は，極板が接地されているかどうかで違いが生じます．

MXK さんのレス (2006/08/20(Sun) 01:29)

そうですね． もともとコンデンサに蓄えられている電荷の大きさを Q，コンデンサの容量を C，回路の対地容量 C_0，とすると，条件 q/Q << C_0/Cが必要ということですね．

山旅人 さんのレス (2006/08/20(Sun) 12:14)

皆さん，こんにちは．私にも加わらせてください．スレッド初出から読んでおりましたが，指摘されているように問題文の不備が伺われ （最終的には，私は 「不備はない」 と考えています），出題意図も計りかねておりました．皆さんのレスを読ませていただき，考えたことを書きます．

（第1） 「Ｘ→0 のとき正極版 0，負極板 q 」 は，私もこれで正しいと思います．

（第2） yama さんが指摘されている接地について 回路は接地されていないようですが，電池がつながれています．電池は無尽蔵の電荷供給体でしょう．MKX さんは，「−q の電荷は電池の付近に押しやられている」 と書いておられますが，私はもう一歩進めて，「電池に吸収されてしまう」 としてよいと考えます． ただし，これは，接地がないからこのように解釈せざるを得ないということで，yama さんの上の一連の指摘は全くその通りだと思います．

（第3） 問題全体として 私は，(1) と (2) は別の問題として独立させるべきだと思います．問題文には， 「q の大きさは…非常に小さい」 と慎重に書かれてはいるものの，(2) があることにより，(1) を解く受験生に無用の戸惑いを与えると思います． また，(2) は誘導に従えば連立方程式を解くだけのものとはいえ，近似の背景にある考え方は明らかに高校の範囲を超えるものでしょう． ただし，入試問題にはこのような問題がまれに出題されているとはいえ，その価値を十分に咀嚼せずに問題集に取り上げた出版社（予備校？）の方が責任は大だと思います．

ところで，（第4） >> yamaさん > 極板が十分広くて端のほうの電荷分布を考えないなら，そのようになりそうです．この場合，内側の電荷分布は，両極板が接地されている場合と同じですね． についてですが，状況を今少し単純化して 『帯電（ｑ）小球のそばに（広がりに比べれば十分薄いが）厚みがある金属板を１枚置く場合』，この金属板を(1)接地した場合と(2)しない場合について，私は，『内側の』 電荷分布は異なると思うのですが，如何でしょうか．（必ずしも全幅の自信はないのですが…）

yama さんのレス (2006/08/20(Sun) 15:23)

>回路は接地されていないようですが，電池がつながれています．電池は無尽蔵の電荷供給体でしょう．MKX さんは，「−q の電荷は電池の付近に押しやられている」 と書いておられますが，私はもう一歩進めて，「電池に吸収されてしまう」 としてよいと考えます．

電池を電荷供給体と考えていいかどうかは疑問です．確かに電池は負極から電子を送り出しているので，負電荷を供給しているように見えますが，一方では，正極から電子を取り入れています．つまり，正極から取り入れた電子を負極から送り出しているだけです．従って電荷の収支は0になるので，電荷を供給しているとは言えないと思います． （正極から電子を取り入れずに，負極から電子を送り出すなら，負電荷を供給することになるでしょうが・・・．） しかし，電荷が「電池に吸収されてしまう」ことはありうるかもしれません．そうなると，電池内部で正負のイオンのバランスがくずれることになりますね．その場合は電池内部の化学反応が関係してくるかもしれないし，そうなると電気容量の概念はあてはまらないかも・・・などと考えるのですが，はっきりしたことは分かりません．

>『帯電（ｑ）小球のそばに（広がりに比べれば十分薄いが）厚みがある金属板を１枚置く場合』，この金属板を(1)接地した場合と(2)しない場合について，私は，『内側の』 電荷分布は異なると思うのですが，如何でしょうか．（必ずしも全幅の自信はないのですが…）

その場合は異なると思います． ２枚の金属板のちょうど中間に電荷があるという特別な場合に限って，接地した場合としない場合の内側の電荷が等しくなります． 金属板が２枚あっても，電荷の位置がその中間からずれている場合は，接地の有無によって内側の電荷は異なってきます．

MXK さんのレス (2006/08/20(Sun) 20:49)

電池付近と書きましたが，正確には対地容量の大きい場所というべきでした．一方，電池に不平衡な電荷を吸収する機能を期待することは無理だと思います．正確にモデル化するなら，回路のどこかを大きい容量のコンデンサを通して接地することになるのでしょう．現実には電極背面，配線，電池などがその役目をしているのですが...

ともかく，qが十分小さいと書いてあるので，問題としては成立していると思います．どれほど小さければいいかと問われると，ここでの議論のようになるわけですね．

yama さんのレス (2006/08/20(Sun) 23:24)

>金属板が２枚あっても，電荷の位置がその中間からずれている場合は，接地の有無によって内側の電荷は異なってきます．

と書きましたが，金属板が接地されてなくても，それらが導線でつながっている場合は，金属板が両方とも接地されている場合と，内側の面の電荷分布は同じになるようです． なお，片方が接地されていて，もう一方がそれに導線でつながっている場合は，両方とも接地されていると見なしていいでしょうね．

レインマン さんのレス (2006/08/20(Sun) 23:31)

こんにちは 質問したレインマンと申します． 始め解説を 最初系全体は中性であるので-qの電荷を極板間におくと 両極板に-ｑ/2の電荷が現れと誤読していました やっぱり気になって解説をもう一度読み直してみたのです そうすると 最初系全体は中性であるので-qの電荷を極板間におくと 両極板[の外側（互いの極板と反対側）にとも）]に-ｑ/2の電荷が現れ の[ ]の部分をなぜか読み飛ばしていました 理解できなかったから無意識に読み違えたのかもしれませんが これは山旅人さんとyamaさんの考えと一致しています これは解説を十分よまなかった私に問題があると思います 本当に申し訳ありませんでした

ｙama さんのレス (2006/08/21(Mon) 09:07)

私は，はじめは内側の面に正電荷が誘起されるのにともなって，外側の面に負電荷が誘起されるのではないかとも考えました．ところが，両方の金属板が導線（と電池）でつながっていることを正しく考慮することができなかったため，内側の面に誘起される電荷が解答と合わなくなりました． そのため，どこかが接地されていなくてはいけないと考えたわけです． しかし，金属板がつながっていることをきちんと考慮すると，内側の面の電荷は，両方の金属板が接地されている場合と同じになり，解答と一致します． 結局，問題の不備ではなく，私の考えが間違っていたということで，お詫びとともに訂正させていただきます． なお，これは導線や電池の電気容量を0と考えた場合ですが，実際はMXKさんの御指摘のように，外側の面とは限らず，回路の適当な部分に負電荷がたまることになるでしょうね．

ところで，解説にあるように，両極板の外側に -q/2 の電荷が現れる理由は分かるでしょうか？ 電荷が両極板の中間にある場合だけでなく，どの位置にあっても，両極板の外側には -q/2 の電荷が現れるのですが・・・． 両極板が導線でつながっていることがキーポイントとなります．考えてみてください．

レインマン さんのレス (2006/08/22(Tue) 23:31)

１時間くらい考えて何とかそれらしい答えが出ました

まず正極版の外側にたまっている電荷をｘ 負極版の外側にたまっている電荷をｙ とおくとｘ+ｙ＝-ｑ?が成り立ちます 負極板と正極板のまんなかの電位をそれぞれ0[V],v[V]とおきます また負極板と電池の負極側の間の電位をV'とおきます

ｘ＝C（ｖ-V)? ｙ＝CV’? ｖ＝V'+V?

?を?に代入すると ｙ＝C（ｖ-V)?’

よってｘ＝ｙ?

?，?より ｘ＝ｙ＝-ｑ/2 まんなかの電位を勝手においていいのか迷いました 最初ｖを求めようといろいろ考えたのですが無理でした コンデンサーの中に-ｑの電荷をおいた時 ｖが上の結果より ｖ＝V-ｑ/2C なので正極板内側に貯まっているる電荷が Q-ｑ/2となり答えと合わないのでぜんぜん自信がありません ところでコンデンサー内に-ｑの電荷をおいた時極板内の電位はどのように なるのでしょうか？

ｙama さんのレス (2006/08/23(Wed) 09:59)

残念ながら根本的に間違っているようです． まず，極板は導体なので，電流が流れていない場合は極板内に電場は存在しません．従って極板内全体にわたって電位は一定になります．「まんなかの電位」も表面の電位も同じになるわけです． また，２枚の極板を電池につないだときは，電荷は内側の面だけに現れ，外側の面には現れません．従って，外側の面に現れる電荷を電池の電圧に関係づけることはできません． この問題で，外側の面に現れる電荷は，極板間の荷電粒子によって誘起されるものです．

誘起される電荷だけを考える場合は，電池の存在は関係ありません．つまり，電池はないものとして，導線でつながれた２枚の極板の間に荷電粒子を置いたと考えればいいのです． 実際の電荷分布は，荷電粒子がないものとして電池につないだときの電荷分布と，電池がないものとして，荷電粒子を置いたときに誘起される電荷分布との重ね合わせになります．設問(2)の(イ)では後者だけが問題になっているわけです．

というわけで，導線でつながれた２枚の極板の間に荷電粒子（-q）を置いたときの電荷分布を考えましょう． このとき，極板間の電気力線の状態を考えると，両極板の内側の面に正電荷が誘起されることがわかるでしょう．そして極板が十分広ければ，誘起される正電荷は，両極板を合わせて+qになることもわかると思います． ここでもし両極板が接地されていれば，誘起される電荷はこれだけです．そして荷電粒子の作る電場と誘起された電荷の作る電場が，極板内でちょうど打ち消しあって極板内の電場が0になります．

しかし，この問題では，極板が接地されていないので２枚の極板全体の電荷が0に保たれないといけません．そのため，-q の電荷がどこかに分布することになります． この-qの電荷は，全体として，極板内の電場を0に保つように分布しなければなりません．そのためには，両極板の外側の面に -q/2 ずつの電荷が（端のほうを除いて）一様な密度で分布すればいいことが分かります． 実際このように分布すれば，一方の極板の外側の電荷が作る電場と，もう一方の極板の外側の電荷が作る電場とが，極板内でちょうど打ち消しあうことが分かるでしょう． （荷電粒子がないものとして，導線でつながれだ２枚の極板に電荷 -q を与えたときの電荷分布を考えてもいいでしょう．）

（備考） この問題では，両極板が導線でつながっているので，両極板全体で電荷が0になればいいのですが，もしつながっていなければ，それぞれの極板の電荷が単独で0にならないといけないので，話が違ってきます． その場合は，両極板を合わせると内側の面全体では -q の電荷が誘起されるのは同じですが，それぞれの極板の内側の面の電荷は，（荷電粒子が両極板のちょうど中間にある場合を除いて）極板が接地されている場合と違ってきます．

レインマン さんのレス (2006/08/23(Wed) 20:20)

理解できましたyamaさんありがとうございました金属内の電場が０になることは授業でやったはずなのに忘れてました． 電池と荷電粒子をまとめて考えようとしたのでこんがらがってしまったようです．

両極板の外側に-ｑ/2ずつたまる理由は，両極板の外側に-ｑ/2ずつたまらないと電界ができて-ｑ/2ずつに戻ろうとするわけですよね また質問ですが極板間電位差と両極板にかかっている電圧は等しくなければならないんですよね?

yama さんのレス (2006/08/23(Wed) 22:29)

>両極板の外側に-ｑ/2ずつたまる理由は，両極板の外側に-ｑ/2ずつたまらないと電界ができて-ｑ/2ずつに戻ろうとするわけですよね

その通りです．

>また質問ですが極板間電位差と両極板にかかっている電圧は等しくなければならないんですよね?

電圧とは電位差のことなので当然そうなります．また，電池の起電力にも等しくなります． 電池がなくて両極板が導線でつながれているだけならば，両極板の電位が等しく，電位差は0ですが，間に電池があると電池の起電力に等しい電位差が生じることになります．