歯車切下げ三角関数関係式

歯車切下げ三角関数関係式

歯車太郎 さんの書込 (2006/08/14(Mon) 09:48)

はじめまして．

小生は歯車歯形の幾何学に詳しい者ですが， 数年前，妙な三角関数関係式を見つけました． 歯車の切下げの幾何の数式を展開している際，

1-sin(t) = cos(t)*cos(t) - tan(pi/4-t/2)*sin(t)*cos(t)

となる関係式を発見しました． そこで，右辺から左辺を導こうとして過去二度企んで見ましたけど， 失敗しました．

ただ，

#include <stdio.h> #include <conio.h> #include <math.h>

main() { double t,f1,f2, pi=3.141592654;

t=158*pi/180; f1 = 1-sin(t); f2 = cos(t)*cos(t) - tan(pi/4-t/2)*sin(t)*cos(t); printf("n n t = %lf deg, f1 = %lf, f2 = %lfn",t*180/pi,f1,f2) ; getch(); }

のようにコンピュータで数値を代入して 当関係式が成り立っていることが分かっています．

もしや，当関係式を証明(右辺から左辺を導く)出来る方は いらっしゃいませんでしょうか． ひとつ，お願い致します．

Re: 歯車切下げ三角関数関係式

Chappy さんのレス (2006/08/14(Mon) 11:19)

歯車太郎さん，はじめまして．Chappyというものです． さっき目覚めたばかりで，朝からおもしろそうな数学の計算ができるのが，嬉しかったです．．．

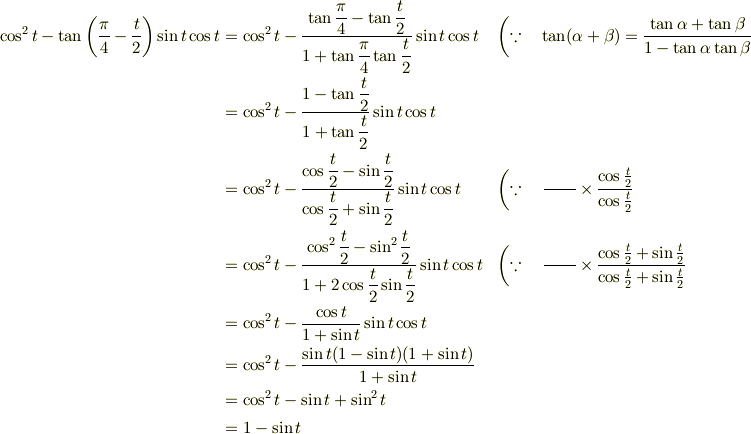
\cos^2t-\tan\left(\frac{\pi}{4}-\frac{t}{2}\right)\sin t\cos t &=\cos^2t-\frac{\displaystyle \tan\frac{\pi}{4}-\tan\frac{t}{2}}{\displaystyle 1+\tan\frac{\pi}{4}\tan\frac{t}{2}}\sin t\cos t & & \left(\because\quad\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta} \right.\\&=\cos^2t-\frac{\displaystyle 1-\tan\frac{t}{2}}{\displaystyle 1+\tan\frac{t}{2}}\sin t\cos t \\&=\cos^2t-\frac{\displaystyle \cos\frac{t}{2}-\sin\frac{t}{2}}{\displaystyle \cos\frac{t}{2}+\sin\frac{t}{2}}\sin t\cos t& & \left(\because\quad\frac{\phantom{\sin t}}{\phantom{\cos t}}\times\frac{\cos\frac{t}{2}}{\cos\frac{t}{2}} \right.\\&=\cos^2t-\frac{\displaystyle \cos^2\frac{t}{2}-\sin^2\frac{t}{2}}{\displaystyle 1+2\cos\frac{t}{2}\sin\frac{t}{2}}\sin t\cos t& & \left(\because\quad\frac{\phantom{\sin t}}{\phantom{\cos t}}\times\frac{\cos\frac{t}{2}+\sin\frac{t}{2}}{\cos\frac{t}{2}+\sin\frac{t}{2}} \right. \\&=\cos^2t-\frac{\cos t}{1+\sin t}\sin t\cos t \\&=\cos^2t-\frac{\sin t(1-\sin t)(1+\sin t)}{1+\sin t} \\&=\cos^2t-\sin t+\sin^2t \\&=1-\sin t

Re: 歯車切下げ三角関数関係式

なんとなく さんのレス (2006/08/14(Mon) 11:26)

はじめまして，なんとなくです．

かなりのプログラマで実力もおありそうなので，おそらく何か単純な計算ミスでしょう．普通に加法定理その他で簡単に証明できます． すでに解答は得ていますが，他の人も計算中のようなので，必要がなければアップしませんね． 歯車の動画，面白いですね．ではまた．

Re: 歯車切下げ三角関数関係式

歯車太郎 さんのレス (2006/08/14(Mon) 21:43)

どうも有難うございました． それにしても，全くの驚きですね． 返信が載せられた時刻からして 即座解いたということに成りますね． 載せられた数式展開での三，四行目のやり方が決め手となる訳ですね．

Re: 歯車切下げ三角関数関係式

Chappy さんのレス (2006/08/15(Tue) 00:00)

いやぁ，１０時５０分くらいに起きたんです，，，ぐーたらしてました (^^; 寝坊はしましたが，おかげさまで，数式がうまく展開できたので，幸せな気分になったというわけであります． ちょっとだけ救われました，，，明日はちゃんと起きようと思います．