長方形が張る立体角の求め方がわかりません
長方形が張る立体角の求め方がわかりません
NK さんの書込 (2006/08/10(Thu) 05:52)
長方形{-a≦x≦a,-b≦y≦b,z=0}が点P(0,0,c)に対して張る立体角の求め方を知りたいです.
電磁気学で,面密度σで帯電している平面S(長方形)がつくる電場を求める問題に出会ったのですが,解けませんでした.
立体角は
dΩ = {dScosθ}/r^2 = c {(x^2+y^2+c^2)}^{-3/2} dxdy
を積分すればいいのはわかるのですが,積分できる気がしないんです….何か他の方法で立体角を求めることはできないんでしょうか?
Re: 長方形が張る立体角の求め方がわかりません
CO さんのレス (2006/08/10(Thu) 15:55)
> 積分できる気がしないんです….
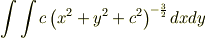
が積分できない,という意味でしょうか?
NKさんがやっている問題でそういう積分が出てくるのかどうかは知りませんが,上の積分は  について積分すると
について積分すると
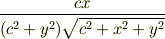
というように積分できるみたいですよ.  についても積分できるみたいです.
についても積分できるみたいです.
積分は http://integrals.wolfram.com/index.jsp にやってもらいました. (^^;
Re: 長方形が張る立体角の求め方がわかりません
toorisugari no Hiro さんのレス (2006/08/10(Thu) 16:18)
COさん その先の計算が私には出せなかったので,先ほどwithdraw したのですが,Mathematicaさんは「初等的にだせる」とおっしゃったのでしょうか.
ちなみに分子は 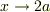 分母は
分母は 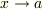 ですよね.
ですよね.
Re: 長方形が張る立体角の求め方がわかりません
CO さんのレス (2006/08/10(Thu) 16:37)
> toorisugari no Hiro さん
Mathematica さんに聞くことはできませんでしたが, 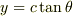 と置いてやり,その後でてくる積分もさらに置換してやると初等的に出すことができると思います.
と置いてやり,その後でてくる積分もさらに置換してやると初等的に出すことができると思います.
Re: 長方形が張る立体角の求め方がわかりません
toorisugari no Hiro さんのレス (2006/08/10(Thu) 17:00)
ううう.でません. Mapleさんに聞いたら,一応初等的だけどarcsinやら根号が複雑にからまった式になってしまいました.追いかけれそうにありません.
教えていただけませんか?
Re: 長方形が張る立体角の求め方がわかりません
toorisugari no Hiro さんのレス (2006/08/10(Thu) 17:34)
> ううう.でません.
どなたか,
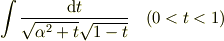
を解ける方いらっしゃいませんか? 解き方おしえてください.
ちなみに答えは
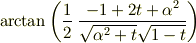
になるようです.
Re: 長方形が張る立体角の求め方がわかりません
なんとなく さんのレス (2006/08/10(Thu) 18:44)
初めまして,toorisugari no Hiroさん.
I=∫dt/{√(α^2+t)√(1-t)}の計算ですが,以下のようになりました. I=∫dt/√(α^2-α^2t+t-t^2) =∫dt/√[-{t+(α^2-1)/2}^2+(α^2+1)^2/4] =∫du/√(a^2-u^2)(∵a=(α^2+1)/2,u=t+(α^2-1)/2と置いた) =arcsin(u/a) =arcsin{(-1+2t+α^2)/(α^2+1)}
なんか,答えが違うようですが,arcsinとarctanの間の関係式からでるかしら?
ちなみに,∬(x^2+y^2+c^2)^(-3/2)dxdyの解は 4arcsin(ab/{√(a^2+c^2)√(b^2+c^2)}) ですね.
Re: 長方形が張る立体角の求め方がわかりません
なんとなく さんのレス (2006/08/10(Thu) 19:04)
確認しました.同じですね.
arcsin(θ)=arctan{θ/√(1-θ^2)}から,arctanで書けば arctan{1/2・(-1+2t+α^2)/√[(α^2+t)(1-t)]} となって,一致しました.
Re: 長方形が張る立体角の求め方がわかりません
CO さんのレス (2006/08/10(Thu) 19:24)
そう簡単には計算できないようですね,すみません. とりあえずその積分計算はかように大変です・・・.
> NK さん
そもそも,なぜそのような積分(立体角?)が出てきたのかも書いていただけますでしょうか.
Re: 長方形が張る立体角の求め方がわかりません
toorisugari no Hiro さんのレス (2006/08/10(Thu) 19:54)
なんとなくさん,ありがとうございます.
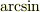 のほうが
のほうが 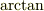 より簡単ですね.(最終結果も,書きませんが,前者で解いた方がきれいでした.)
より簡単ですね.(最終結果も,書きませんが,前者で解いた方がきれいでした.)
結果が
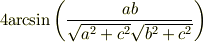
ですか.形がきれいですね.
垂辺を  ,底辺を
,底辺を 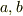 とした,ふたつの直角三角形の底辺に対する角度を
とした,ふたつの直角三角形の底辺に対する角度を 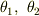 とすると,
とすると,
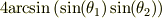
となりますね.ある意味きれいですね.
Re: 長方形が張る立体角の求め方がわかりません
toorisugari no Hiro さんのレス (2006/08/10(Thu) 22:59)
> ある意味きれいですね.
予定調和で解けないか,試してみました.あまり簡単ではなかったです....
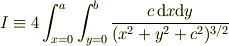
に対して
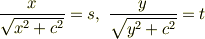
と置き換えると,鬱陶しい計算を経て,積分は
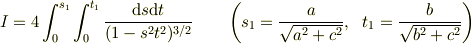
となります.
ここで
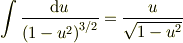
( 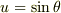 と置き換え変形する.途中
と置き換え変形する.途中 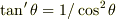 を使う.)
だから,求める値は
を使う.)
だから,求める値は
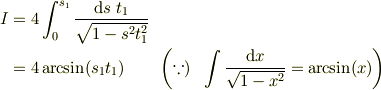
となります.
Re: 長方形が張る立体角の求め方がわかりません
なんとなく さんのレス (2006/08/11(Fri) 11:00)
>toorisugari no Hiroさん.
こんにちは.
なるほど,面白いアプローチです. 微積分(方程式)の解と境界の形状はディリクレ問題として密接な関係があるのでしょうが,浅学にして分かりません.でもきれいな(対称性の高いあるいは座標系にマッチした)領域に対する解はやはり対称性が高くなることが期待されますね. 複素積分とも関わりますが,このような積分の背景に正則性,あるいはC∞級の関数の持つ性質が見え隠れしているようです. スレ主の疑問のように,次元を落とした計算方法が何かあるような・・・やはり数学は奥が深い(いや,私が浅い(^o^;)だけ).
訳の分からない問答でしたが,また,よろしく.
Re: 長方形が張る立体角の求め方がわかりません
toorisugari no Hiro さんのレス (2006/08/11(Fri) 18:37)
なんとなくさん コメントありがとうございます.
> スレ主の疑問のように,次元を落とした計算方法が何かあるような
昨日いろいろ考えましたが,あまり芳しくありません.
位置ベクトルを  ,その方向の単位ベクトルを
,その方向の単位ベクトルを 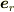 とします.位置
とします.位置  にある微小面積素
にある微小面積素 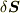 が原点に対して張る立体角は,面積素を半径
が原点に対して張る立体角は,面積素を半径 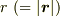 の球面に射影してできる領域が,原点に対して張る立体角と等しいから,微小立体角は
の球面に射影してできる領域が,原点に対して張る立体角と等しいから,微小立体角は
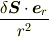
で表されます.これの積分が,スレ主さんの出した問題ですね.
積分が閉曲面ならガウスの定理から答えは 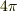 の整数倍となり簡単なのですが,開曲面の場合はそれが使えません.
の整数倍となり簡単なのですが,開曲面の場合はそれが使えません.
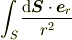
にストークスの定理を適用できれば線積分に持ち込めるのですが... そのためには,
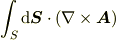
という形にしなければなりません.なお,
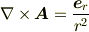
を満たす 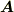 はDiracの磁気単極子(magnetic monopole)の作るベクトルポテンシャルそのものです.これが得られれば,
はDiracの磁気単極子(magnetic monopole)の作るベクトルポテンシャルそのものです.これが得られれば, 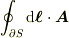 を計算するだけですね.一応.
を計算するだけですね.一応.
原点以外で  を満たしますから,原点から無限遠までのびるある曲線以外の空間(あるいは半空間)で
を満たしますから,原点から無限遠までのびるある曲線以外の空間(あるいは半空間)で 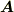 は存在します.極座標系なら,
は存在します.極座標系なら,
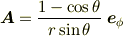
が知られています.(ただし, 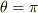 に特異性があります.)
に特異性があります.)
しかし,これを使って 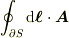 を計算する気は....おきません.
を計算する気は....おきません.
すなおに, 曲線と曲面の微分幾何 小林 昭七
を読んだ方が早いかな?
Re: 長方形が張る立体角の求め方がわかりません
NK さんのレス (2006/08/12(Sat) 11:32)
皆さん,ありがとうございます.
>COさん
面Sが点Pに対して張る(あるいはPがSを見る)立体角Ωは,Sを底面,Pを頂点とする錐面が,Pを中心とする単位球面から切り取る面積を意味し,一般に,点  にある微小面積dSが原点Oに対して張る立体角dΩには,次の関係があります.
にある微小面積dSが原点Oに対して張る立体角dΩには,次の関係があります.
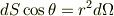
ここで  は面dSの法線
は面dSの法線 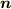 とベクトル
とベクトル  のなす角で,左辺はdSの
のなす角で,左辺はdSの  方向への射影です.
方向への射影です.
一般に,xy平面上にある任意の形の板に一様な面密度σで電荷が分布しているとき,任意の点Pにできる電場のz成分は,Pがその板を見る立体角Ωにより
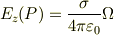
と表されます.
このため立体角を求めて電場を求めたかったのですが,積分が難しいので,こちらに書き込みをさせていただきました.
立体角が
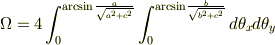
であると考えると,積分結果は
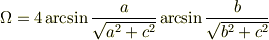
となり,答えが間違いになってしまいました.なぜでしょうか?(いい方法を思い付いたと思ったんですけど・・・.)
電場を求めるのに,電位を求めてから微分する方法もありますが,電位を求めるための積分もなんか難しそうな気がします・・・.
Re: 長方形が張る立体角の求め方がわかりません
toorisugari no Hiro さんのレス (2006/08/12(Sat) 12:00)
NKさん :
> 答えが間違いになってしまいました.なぜでしょうか?(いい方法を思い付いたと思ったんですけど・・・.)
それで解けたら,苦労はしません.第一 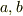 が十分大きいと,
が十分大きいと, 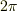 でなく
でなく 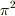 になってしまいます.
になってしまいます.
- 何故そうなるかは,うまく言えませんが,元の式からはとうてい
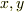 が分離できるようにはみえませんね.
が分離できるようにはみえませんね.
> 電位を求めてから微分する方法もありますが,電位を求めるための積分もなんか難しそうな気がします・・・.
やってないので保証できませんが,一般には電位からの方が楽です.
Re: 長方形が張る立体角の求め方がわかりません
CO さんのレス (2006/08/12(Sat) 13:49)
> NK さん
> 一般に,xy平面上にある任意の形の板に一様な面密度σで電荷が分布しているとき
> 任意の点Pにできる電場のz成分は,Pがその板を見る立体角Ωにより
> 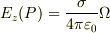 > と表されます.
> と表されます.
なるほど,そういう公式があったのですね.(厳密になりたつのでしょうか?) 私は素直に xy 平面上の電荷分布が作り出す電場を重ね合わせることを考えていました. # この問題は電位を求めて微分計算すればできると思います.
Re: 長方形が張る立体角の求め方がわかりません
なんとなく さんのレス (2006/08/12(Sat) 15:21)
こんにちは.
くだんの公式,E=σΩ/4πε0は,磁場では,円電流または磁気モーメントによる磁位V=IΩ/4π=MLΩ/4πμ0(等価板磁石)として知られている公式ですね. 美しい公式だと思います.任意の領域によるポテンシャルがその領域を見込む(ほぼ)立体角のみで書ける,すばらしい. ただ,実際の計算は簡単ではないのが残念.
>toorisugari no Hiroさん 磁気単極子ですか,なるほど!.興味は尽きないけれど,手に負えませんなあ(^o^;)>.
Re: 長方形が張る立体角の求め方がわかりません
山旅人 さんのレス (2006/08/12(Sat) 15:47)
横から失礼致します.(TeX を使えないので,見づらくてすみません.)
立体角として捉えるのが現代的なのでしょうが,私は (CO さんがおっしゃるように) 素朴に電場を重ね合わせて考えた方がわかりやすいです.
点 Q(x 0 ,y 0 ,0) にある点(=微小領域)電荷 σdxdy が P(0,0,c) につくる電場の z 成分 E z (P) は,
E z (Q)=(1/4πε 0 )σdxdycosθ/r 2 (ただし,r=PQ=√(x 0 2 +y 0 2 +c 2 ),θ は∠OPQ ) =(1/4πε 0 )σcdxdy/r 3 …(1)
(1)を −∞<x<∞ で積分することにより,y 軸に垂直な無限長直線L(y=y 0 ) が P につくる電場の z 成分 E z (L) は,
E z (L)=∫ -∞ ∞ E z (Q)dydx =(σc/4πε 0 )∫ -∞ ∞ [dy/(x 2 +y 0 2 +c 2 ) 3/2 ]dx =(σc/4πε 0 )・dy/(y 0 2 +c 2 )・2…(2)
(2)を −∞<y<∞ で積分することにより,無限平面が P につくる電場の z 成分 E z は,
E z =∫ -∞ ∞ E z (L)dy=(σc/2πε 0 )∫ -∞ ∞ dy/(y 2 +c 2 ) =(σc/2πε 0 )・π/c =<b>σ/2ε 0 </b>
最後の結果に平面からの距離 c が入らないとを確認すべきです.もっとも,そのことを示すだけならばガウスの定理で一発ですが.
Re: 長方形が張る立体角の求め方がわかりません
yama さんのレス (2006/08/12(Sat) 21:29)
任意の点(x,y,z)の電場を求めるのだったら,電位を求めてからその勾配を計算するほうが簡単な場合が多いと思います. しかし,特定の点たとえば(0,0,c)の電場を求める場合は,電位から求めるほうが簡単だとは必ずしも言えないと思います. というのは,1点の電位の値だけからその点の電場を計算することはできないからです.電場を計算するには,その点を含む微小領域の任意の点(x,y,z)の電位を求め,x,y,zで偏微分してから,x=0,y=0,z=c などと置く必要があるからです.
ただし,今回の問題に限れば,対称性からx成分とy成分が0になることが予め分かっているので,点(0,0,c)のポテンシャルをcで微分して,電場のz成分を求めることができるでしょう.この場合電場を直接求めるのと比べてどちらが簡単かは微妙ですね.
Re: 長方形が張る立体角の求め方がわかりません
NK さんのレス (2006/08/12(Sat) 23:29)
皆さん,ありがとうございます.
>toorisugari no Hiro さん やっぱりそうですよねー….あってるわけがないと思いながら,そうであってほしいなという願望が働いてしまいました.無理やり正しい積分結果が出せるような方法を考えてたんですが,あきらめて正攻法でやってみようと思います.
立体角による表現は,少しイメージしにくいですが,美しいので個人的には好きです.それに,電位から電場を求めるより,電場を直接求めたい性分です.でも柔軟に対応する方がいいことがこの問題でわかりました.
結局,電位の積分計算もうまく解けないんですけどw.