摩擦力と力学的エネルギー
摩擦力と力学的エネルギー
はる さんの書込 (2006/08/08(Tue) 23:37)
こんばんは. 現在高三で日夜勉強中です・・・ 解説を読んでもよく分からないので,質問してもよろしいでしょうか? 先日物理の問題を解いていたとき, 台(質量M)と小物体(質量m)の間の摩擦係数がμで,小物体が台の上を距離dだけ滑ったとき,2物体の力学的エネルギーの和は,−μmgd減少する,と解説に書いてあったのですが,台が滑らかな床に乗っていて,台,小物体ともに違う速度で運動していた場合,台の上をd滑っても,床から見たときにはd滑ったことにはならないと思うのですが, その場合も−μmgとなるのでしょうか?
Re: 摩擦力と力学的エネルギー
mNeji さんのレス (2006/08/08(Tue) 23:53)
はじめまして.
受験勉強,お疲れ様です.
まず,味噌は >(質量M)と小物体(質量m) >台が滑らかな床
おそらく,問題が不完全なのだと思いますが,この場合,
・ 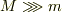 を仮定して良いのだとおもいます.
を仮定して良いのだとおもいます.
すると,台は,床からも摩擦力がないので,小物体がその上で少し動いても,事実上,慣性系とみなせるので, ・小物体が止まるまでの仕事=摩擦力*制動距離 で良くないですか?
Re: 摩擦力と力学的エネルギー
toorisugari no Hiro さんのレス (2006/08/09(Wed) 00:05)
たぶん,仕事の定義に現れる距離が,相対的に動いてる座標系からみたとき変わるので,エネルギーの消費の計算がふたつの座標系で違うように思われることをおたずねとは思うのですが,
質問の意図がいまいち分からないので,まず,問題の全文を載せてください.
# ちなみに「−μmgd減少する,」は変な表現です.(実際には力学的エネルギーの和は増えていることになります.)
Re: 摩擦力と力学的エネルギー
はる さんのレス (2006/08/09(Wed) 00:53)
早速のお返事,どうもありがとうございます. 問題文は, 質量Мの台車が滑らかな床の上にあり,その左端に質量mの小物体が乗っている. 台車と小物体のあいだの動摩擦係数はμである. 小物体を瞬間的に押して,水平に初速度vで打ち出したところ,しばらくすると小物体は台上で台に対して,台上の左端から距離dで静止して,その後一体となって速さVで運動した. 大事な部分はこんな感じだと思いますが,このとき床に静止した観測者からみたときには,d以上滑ってると思うのですが,このときでも台が床に固定されてるときのように力学的エネルギーの和がμmg減少するのかな? ということです.
Re: 摩擦力と力学的エネルギー
ZZZ さんのレス (2006/08/09(Wed) 03:07)
はじめまして.
減少した運動エネルギー(=摩擦面がした仕事)は摩擦のある面をどれだけの距離滑ったかで決まります.
よって距離dだけ摩擦面を滑れば,摩擦力×dが運動エネルギーの減少量ということになります.
大事なのは摩擦面上を滑った距離で,トータルで小物体が移動した距離ではありません.
Re: 摩擦力と力学的エネルギー
mNeji さんのレス (2006/08/09(Wed) 03:41)
t=0の時,静止系の座標原点Sが台の左端とし右にむかって 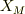 ,台の左端から見た小物体の座標を
,台の左端から見た小物体の座標を 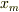 と定めます.従って,静止系からみた小物体の座標は;
と定めます.従って,静止系からみた小物体の座標は;
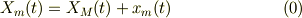
題意より
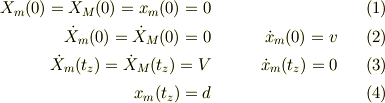
静止系から見た運動方程式は;
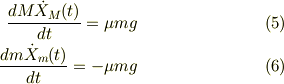
式(5)は
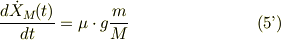
で,式(6)では,式(0),式(5')を留意して整理すると
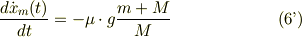
式(5')(6')の両式とも,定加速運動を示している.式(6)を初期条件,式(2)のもとで求めると,
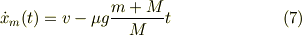
小物体が静止する時間 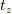 では,式(3)が成立するから
では,式(3)が成立するから
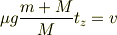
故に

式(7)を時刻0から 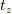 まで積分すると,式(8)と式(4)より
まで積分すると,式(8)と式(4)より
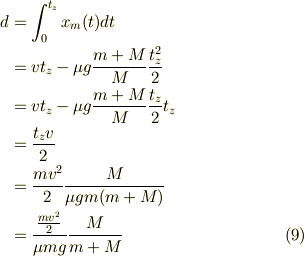
式(5')の積分し,初期条件,式(2)を顧慮すると

式(3)のように, 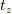 の時,台も加速が終了するので,
の時,台も加速が終了するので,
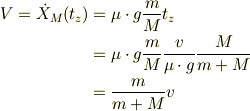
従って,運動エネルギの減少量は,式(9)を考慮して
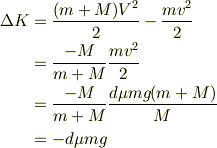
と,通常の小物体が理想的な床面を滑って,止まる時の運動エネルギと同じ形式の損失が出てくる.ただし,dは式(9)で 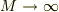 とした値である事に注意するべきだ.そこで,
とした値である事に注意するべきだ.そこで,
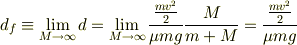
よって,

Re: 摩擦力と力学的エネルギー
はる さんのレス (2006/08/09(Wed) 09:57)
お返事,どうもありがとうございます. やっぱり台上を滑った距離で計算するのですね. 確かにイメージとしては台が固定されていてもいなくても,摩擦力はμmgで一定で, 実際に台の上を滑らないと摩擦熱が発生しないことからも,台の上を滑った距離の分だけ,減少するのはなんとなく分かる様な気もします.m(_ _)m
Re: 摩擦力と力学的エネルギー
toorisugari no Hiro さんのレス (2006/08/09(Wed) 12:34)
はるさんはもう見てはいらっしゃらないかもしれませんが,
> やっぱり台上を滑った距離で計算するのですね.
別に静止系で見た距離で計算してもいいんですよ.相方を忘れなければ.
こういう問題を考えてみてください.
「互いに一定の力  を及ぼし合うふたつの物体A,Bが力が釣り合って静止している.
を及ぼし合うふたつの物体A,Bが力が釣り合って静止している.
単位時間の間にAがする仕事は0だからAの力学的エネルギーは一定.
静止系に対して一定の速度  で移動している観測者がいる.
この系から見たとき,Aは
で移動している観測者がいる.
この系から見たとき,Aは 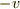 で運動しているので,Aが単位時間にする仕事は
で運動しているので,Aが単位時間にする仕事は 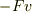 で0ではない.
で0ではない.
『Aの力学的エネルギーは一定』に反していて,矛盾ではないか?」
反していないから,矛盾ではないですよね.(相方をわすれなければ)
Re: 摩擦力と力学的エネルギー
yama さんのレス (2006/08/09(Wed) 12:57)
この問題では,小物体が台上を距離dだけ滑って静止したわけですが,静止しなくても距離dだけ滑ったときには,運動エネルギーの和が μmgd だけ減少します.これは,次のようにして示すことができます.
床に固定した座標系で考えることにします.
まず台の運動を考えると,台には小物体からの摩擦力 μmg がはたらきます.台が床の上を距離 S だけ滑って速度 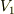 になったとすると,運動エネルギーの変化が摩擦力のした仕事に等しいことから次の式が成り立ちます.
になったとすると,運動エネルギーの変化が摩擦力のした仕事に等しいことから次の式が成り立ちます.

次に,この間に小物体が台上をdだけ滑って,速度 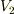 になったとします.このとき,床に対しては S+d だけ動いているので,摩擦力が小物体に対して -μmg(S+d) の仕事をします.
この仕事は小物体の運動エネルギーの変化に等しいので,次の式が成り立ちます.
になったとします.このとき,床に対しては S+d だけ動いているので,摩擦力が小物体に対して -μmg(S+d) の仕事をします.
この仕事は小物体の運動エネルギーの変化に等しいので,次の式が成り立ちます.
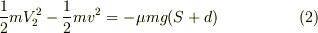
(1)と(2)を足し合わせると次の式が得られます.
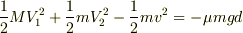 この式は,運動エネルギーの和が μmgd だけ減少することを示しています.
この式は,運動エネルギーの和が μmgd だけ減少することを示しています.
なお,この問題の場合は小物体が台上を d だけ滑って台に対して静止するので, 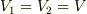 とおくと次のようになります.
とおくと次のようになります.
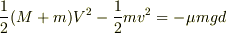
Re: 摩擦力と力学的エネルギー
komagatake さんのレス (2006/08/20(Sun) 12:17)
新しく掲示板の仲間に入れていただきました.どんな内容の質問があるだろうかと思って見ています. もう終わっている内容かもしれませんがちょっと書き込みをさせていただきます.
この問題は元々違う内容だったのではないかなという気がします.勝手に問題を書き換えます.
「水平でなめらかな床の上に質量Mの台がある.台の上に質量mの物体を置き初速度vを与えて運動させた.物体は台の上をd滑った後,台と一体になって運動した.一体となって運動しているときの速さVを求めよ.ただし,重力の加速度の値はg,物体と台との間の運動摩擦係数をμとする.」(私が勝手に作った問題)
この問題は運動方程式で得のは面倒ですが台と物体を1つに考えてエネルギーで考えると楽です.摩擦が原因でしたの台が加速されます.はじめ物体に与えた運動エネルギーが台と物体を合わせたものの運動エネルギーに代わっていくのですが摩擦が台を動かしたのですから摩擦によるロスを考えないといけません.それでこの質問が出てくるのです.だから途中経過の確認だけの問題だということになります.でもそれだけだとあまり面白くありません.
この問題の面白いところは力学の問題によくある「摩擦はないものとする」という表現を使うことが出来ないということです.摩擦がなければこの問題は成り立ちません.摩擦がなければ上の物体は台に無関係にただ滑っていくだけです.面白くも何ともないです.