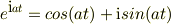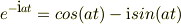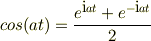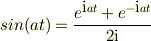媒介変数表示の2階微分に関して
媒介変数表示の2階微分に関して
サンダーSP さんの書込 (2006/08/05(Sat) 00:52)
現在もっと物理数学を習得すべくいろいろ勉強しておりますが,しかしどうしても微分のところで理解できない箇所があるので,基礎的な質問だとは思いますが,回答等をお願いします.(恐らく高校数学の範囲だと思います)
微分された式dy/dxなどは,dy/dx=(dy/du)(du/dx)のように積のように書かれ,演算子(d/dx等)として扱って,演算子の交換則が成り立つとたいてい書かれていますが,タイトルどおり媒介変数表示された場合の2階微分については成り立ちませんでした.
例として,x=sin at,y=e^ktとおいた時,dx=a(cos at)dt,dy=k(e^kt)dtから,dy/dx=k(e^kt)/a(cos at)…(1) yのxについての2階微分,(d^2/dx^2)y=(d/dx)(dy/dx) =(d/dt)(dt/dx)(dy/dx)…(2) =(d/dt)(dy/dx)(dt/dx)…(3) と(2),(3)の2つが出てくるように思えるのですが,実際は(2)と(3)の結果は違い,(3)が正しいみたいですが,なぜそうなるのかが分かりません.
ちなみにそれぞれを計算すると, (2)=(d/dt)(1/a(cos at))(1)=k(sin at)(e^kt)/a(cos at)^3 (3)=(d/dt)(1)/a(cos at)=k(e^kt){k(cos at)+a(sin at)}/a(cos a)^3 ※(1),(2),(3)は関数のように書きました. と明らかに結果が違ってきます.
多分d/dtをdy/dxか,dt/dxのどちらに適用するかで変わるのだとは思いますが・・・.
Re: 媒介変数表示の2階微分に関して
mNeji さんのレス (2006/08/05(Sat) 01:34)
私も,tadashさんのご指摘が有っていると思います.
そもそも,dy/dx=dy/du*du/dx= (dy/du)/(dx/du)ですよね.
Re: 媒介変数表示の2階微分に関して
tadash さんのレス (2006/08/05(Sat) 01:40)
更に(2)式と(3)式は 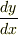 と
と 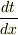 の順番が変わっただけに見えますが・・・
の順番が変わっただけに見えますが・・・
Re: 媒介変数表示の2階微分に関して
サンダーSP さんのレス (2006/08/05(Sat) 01:55)
失礼しました.今度は一応実際の計算用紙の結果を移しながら,もう一度検討して上記の計算を修正が,やはり結果が違ってしまいます.
>>更に(2)式と(3)式はとの順番が変わっただけに見えますが・・・ はい,その通りです.ただ順番を変えただけなのですが,計算結果がなぜか変わってしまいました.
あと,tadashさん,初めまして.
Re: 媒介変数表示の2階微分に関して
tadash さんのレス (2006/08/05(Sat) 08:42)
更に(2)式と(3)式は 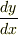 と
と 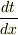 の順番が変わっただけに見えますが・・・
実は,一般に微分演算子の交換関係が成り立たないのですよ,特に量子力学では・・・
詳しくはこのサイト内の量子力学の「演算子と交換関係」のところを見てみてはいかがかしら.
あっ,でも(3)式が正しいとは言い切れないのでは?演算子
の順番が変わっただけに見えますが・・・
実は,一般に微分演算子の交換関係が成り立たないのですよ,特に量子力学では・・・
詳しくはこのサイト内の量子力学の「演算子と交換関係」のところを見てみてはいかがかしら.
あっ,でも(3)式が正しいとは言い切れないのでは?演算子 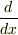 を
を 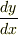 に作用させるのか,
に作用させるのか, 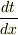 に作用させるのかで意味が異なってくるはずです.
に作用させるのかで意味が異なってくるはずです.
Re: 媒介変数表示の2階微分に関して
サンダーSP さんのレス (2006/08/05(Sat) 09:49)
>>実は,一般に微分演算子の交換関係が成り立たないのですよ,特に量子力学では・・・ 詳しくはこのサイト内の量子力学の「演算子と交換関係」のところを見てみてはいかがかしら.
「演算子と交換関係」のページをまた拝見させていただきました.確かに演算子は行列みたいに交換不可能だそうなのですが,ベクトル解析を勉強していたときに,d/dt(div A)=div dA/dt,という変形があったり,偏微分では(∂/∂u)(∂/∂v)f=(∂/∂v)(∂/∂u)fと書かれていました.(ただ偏微分の方には,最初に『通常の物理で現れる関数の場合』と断りが書かれてましたが.)
>>あっ,でも(3)式が正しいとは言い切れないのでは?演算子d/dxをdy/dxに作用させるのか,dt/dxに作用させるのかで意味が異なってくるはずです.
一応その解答が書かれた問題の例として,持ってない方が多いかもしれませんが,数研出版のチャート式(青),数?−P109などに(d^2/dx^2)y=d/dx (dy/dx)=d/dt (dy/dx) dt/dxとあります.これは(3)の変形と同じです.
Re: 媒介変数表示の2階微分に関して
なんとなく さんのレス (2006/08/05(Sat) 11:03)
こんにちは,なんとなくです.
横やりですが,もう少し単純に考えても良いと思いますよ.
まず,微分演算子は量子力学とは関係なく,「一般に」交換関係は成り立たない. 「一般に」とは,勿論交換してよい場合もある,と言う含みです. つまり,通常は計算の順序を守る必要がある,ということですね. そうすると,x=x(t),y=y(t)なる媒介変数表示において,1階微分は, dy/dx=(d/dx)y(t)=(dt/dx・d/dt)y(t)・・・? となって,y(t)に作用しているのは演算子d/dtです.このとき(dt/dx)はすでに 係数となっています.2階微分はこれを繰り返すのみですから, d^2y/dx^2=(dt/dx・d/dt){(dt/dx・d/dt)y(t)}・・・? と書けます.このとき右辺最初のd/dtは{…}全体に作用しでいます.最初のdt/dx は係数ですので,右辺の最後においても同じです. つまり,正しい式は?であり,交換できる部分があればこれを変形したに過ぎないはずです. そういう目でもとの疑問を見直せば,最初のd/dtがどこまで作用しているのか明確ではないので,どちらも正しいとは言いがたいですね. 特に(2)はどこで作用を切っても,間違いです. (3)は,d/dtがdy/dxまでしか及んでいないなら,正しい答えを導くはずですね. 数研の式は()でd/dtの作用範囲を暗黙的に示し,この計算では係数であるdt/dxを後ろに移動しただけですね.少し惑わす表現です.
まあ,要は演算子の作用の順序は変えないのが原則です.
Re: 媒介変数表示の2階微分に関して
yama さんのレス (2006/08/05(Sat) 12:17)
なんとなくさんが書かれているように演算子d/dtのはたらく範囲を()などではっきり示すことが大切です.
結論としては,なんとなくさんの?式が正しいのですが,係数とd/dtを分けてd/dtが作用した後で係数を掛けるように表したほうが分かりやすいのではないかと思います.
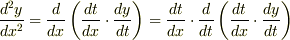 となりますが,()の中の順番を入れ替えて次のように表すこともできます.
となりますが,()の中の順番を入れ替えて次のように表すこともできます.
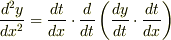 d/dtは()の中全体に作用するのでどちらでも同じです.d/dtの計算を行って次のように表すこともできます.
d/dtは()の中全体に作用するのでどちらでも同じです.d/dtの計算を行って次のように表すこともできます.
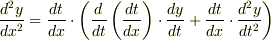
Re: 媒介変数表示の2階微分に関して
yama さんのレス (2006/08/06(Sun) 11:34)
上記の回答はもとの質問からは少しずれていたようです.
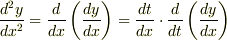 となり,これを変形すると上記のようになるわけです.
この式は次のように表すこともできます.
となり,これを変形すると上記のようになるわけです.
この式は次のように表すこともできます.
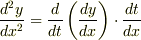 これはサンダーSPさんの(3)式ですね.ただし,(3)式の表し方では
これはサンダーSPさんの(3)式ですね.ただし,(3)式の表し方では
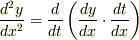 の意味に誤解されるおそれがあります.
(d^2/dx^2)y={(d/dt)(dy/dx)}(dt/dx)
または (d^2/dx^2)y=(dt/dx)(d/dt)(dy/dx)
と表すのがいいでしょう.
なお(2)式は,なんとなくさんのおっしゃる通り明らかに間違っています.
の意味に誤解されるおそれがあります.
(d^2/dx^2)y={(d/dt)(dy/dx)}(dt/dx)
または (d^2/dx^2)y=(dt/dx)(d/dt)(dy/dx)
と表すのがいいでしょう.
なお(2)式は,なんとなくさんのおっしゃる通り明らかに間違っています.
Re: 媒介変数表示の2階微分に関して
サンダーSP さんのレス (2006/08/06(Sun) 17:23)
tadashさん,mNejiさん,なんとなくさん,yamaさんありがとうございました. つまり,丁寧に変形すると,d^2y/dx^2=(d/dx)(dy/dx)で,dy/dx=f(t)=fとおくと,df/dx=(df/dt)(dt/dx)={(d/dt)f}(dt/dx)={(d/dt)(dy/dx)}(dt/dx)という事ですね.
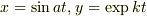 と置いたとき
と置いたとき 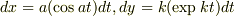 から,
から, 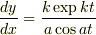 となるはずでは?
となるはずでは?