さち さんの書込 (2006/08/03(Thu) 11:44)

こんにちは．私は高専に通う3年生です． 自分でも考えてはみたのですが，分からない問題があるので質問させてください．

問題は，一様な材質の針金を折り曲げて作った物体AOBの重心の位置座標を求めよ． というものです． OA＝1.6ｍOB＝3.2ｍで，角AOB＝60°です． （Oは原点，Bはｘ軸上にあり，ｙ軸の正の方向にAがあります．）

ここで質問なのですが， 針金部分は一箇所でまげてあり，辺ABは針金ではありません． その場合，この三角形の重心は，辺の全てが針金でできている場合と変わってくるのでしょうか． また，重心の位置座標を解く考え方を教えていただけると嬉しいです．

おねがいします．

toorisugari no Hiro さんのレス (2006/08/03(Thu) 12:31)

後半の質問にお答えします．

ある物体の全質量を ，重心の位置ベクトルを 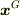とします．

いま，この物体をふたつの部分A,Bに仮想的に分けたとします．(境界はどこでもいいです．また，実際に切断や分離をする必要はありません．頭の中であなたの都合のいいように物体をふたつの部分に分ければいいのです．)

上と同様に 部分Aの質量を 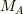，重心の位置ベクトルを 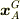， 部分Bの質量を 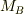，重心の位置ベクトルを 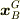とおきます．

これらの変数には

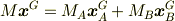
が成り立ちます．(証明に興味があるなら再度質問してください)

これを使えば解けるはずです．

さち さんのレス (2006/08/03(Thu) 13:11)

返信ありがとうございます． 考え方は理解できました． しかし座標平面上で考えることができません； 今，一本の針金が一箇所で折り曲げられていて，一辺がかけた三角形のようになっているとき，どのようにこの考え方を利用したらよいのでしょうか．

一つの辺にだけ着目すればこの解き方で分かるのですが，全体として考えるとどうすればよいのか分からないんです．

申し訳ありませんがもう少しヒントをいただけると嬉しいです．

toorisugari no Hiro さんのレス (2006/08/03(Thu) 13:35)

> しかし座標平面上で考えることができません

?? 重心のx座標，y座標を求めることができないと言うことですか?

> 一つの辺にだけ着目すればこの解き方で分かるのですが

それぞれの辺の重心のx座標，y座標を求めることができれば，

> 全体として考えるとどうすればよいのか分からないんです．

公式に当てはめるだけでは?

三角形にこだわる必要はないと思います．

さち さんのレス (2006/08/03(Thu) 14:16)

そうです． 重心のx座標，y座標を求めることができないんです； Aがｙ軸上にあるのなら，（1.6,0.8）なのですが今の場合だとよくわかりません．

三角形にこだわる必要はないとはどういうことでしょうか・・？

toorisugari no Hiro さんのレス (2006/08/03(Thu) 15:15)

> 重心のx座標，y座標を求めることができないんです； OA＝1.6ｍOB＝3.2ｍで，角AOB＝60°(Oは原点，Bはx軸上，y軸の正の方向にAがある．)ですよね．

1. Aの座標，Bの座標はわかりますか?(絵を書けますか?)
2. 辺OA,辺OBそれぞれの重心の座標および質量はわかりますか?

> 三角形にこだわる必要はないとはどういうことでしょうか・・？

三角形の板なら幾何の知識をつかえますが，3辺のみが質量をもつ三角形の場合，幾何の知識は直接的には関係ありません．まして，2辺しかないのなら三角形にこだわる根拠は私にはわかりません．

> Aがｙ軸上にあるのなら，（1.6,0.8）なのですが

AOBが直角三角形の場合でもおっしゃるようにはなりませんよ．

丁寧に導出を説明してください．

さち さんのレス (2006/08/03(Thu) 15:38)

なんどもお答えして頂いてありがとうございます．

>(1) Aの座標，Bの座標はわかりますか?(絵を書けますか?) 絵はかけます． 1:2:√3をもちいれば座標もだせますが・・ A(3.2,0) B(0.8,0.8√3)でいいのでしょうか．

>(2) 辺OA,辺OBそれぞれの重心の座標および質量はわかりますか? 質量については何もわかりません（問題文に記述がありません）

toorisugari no Hiro さんのレス (2006/08/03(Thu) 16:00)

> A(3.2,0) B(0.8,0.8√3)でいいのでしょうか．

はいOKです．(良かった，これができないと，あとどう説明すればいいか悩むところでした．)

>>(2) 辺OA,辺OBそれぞれの重心の座標および質量はわかりますか? > 質量については何もわかりません

では質量比は?(OAの質量を1としたら，OBの質量は?) あと，重心は?

>（問題文に記述がありません）

ヒントが書いてありますよ．

さち さんのレス (2006/08/03(Thu) 17:02)

＞では質量比は?(OAの質量を1としたら，OBの質量は?) これも1:2:√3ですよね． OAが1ならOBは2です．（全体の重さは3ですか？）

それぞれの辺の重心は中点ですよね・・？ そしたら3(ｘG,ｙG)＝（0.4,0.4√3）＋2（1.6,0）でしょうか？

toorisugari no Hiro さんのレス (2006/08/03(Thu) 19:47)

> OAが1ならOBは2です．（全体の重さは3ですか？） > それぞれの辺の重心は中点ですよね・・？ > そしたら3(ｘG,ｙG)＝（0.4,0.4√3）＋2（1.6,0）でしょうか？

OKです．OA,OBの質量を 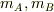とすれば 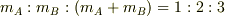となるので上の式 3(ｘG,ｙG)＝（0.4,0.4√3）＋2（1.6,0） がえられます．

これが目的地ですね．おめでとうございます．

さち さんのレス (2006/08/03(Thu) 20:55)

よかったぁ！ 本当に丁寧に教えていただいてすいません． 何度も返信していただきありがとうございました．

komagatake さんのレス (2006/08/19(Sat) 16:56)

ちょっと補足させてもらいます．高等学校で物理を教えているときに「重心は質量のないところに来るときもある」というのがなかなか実感出来なかったようです．この質問をされている方もそうだったのではないでしょうか．弥次郎兵衛を作ってやって見せたのですが．飛び込みの時のようにからがを丸めると重心はお腹のあたりの体の外に来るというのも言ったのですが．生徒は渋々納得という印象でした．計算よりも前にこういう事がネックになっているのではないでしょうか．