愚問ですみません.
愚問ですみません.
歩き目です さんの書込 (2006/08/01(Tue) 22:36)
前回は自分のわからない疑問に付き合っていただき本当にありがとう ございました.今は夏休みですがうかれてもいられないというのが実 情ですね.では,またしても学校のテストでの疑問点です. まずは,設問を書き並べます. 浅い水槽に水を張り,この水面上にx-y座標を設け,0≦x<16cmの範囲 を領域?,16≦x<34cmの範囲を領域?とする.領域?は水深が周囲よ り深く,ここでの水面波の速さは領域?での1.5倍ある.また,領域? と?の境界での反射は考えず,屈折だけが起こるものし,屈折により振 動数が変化することはない.この水面上で水面波を起こす波源はS1,S2 の2つがあり,どちらも振幅0.50cm,振動数1.0Hzで振動して円形波を 作り出す.波源S1,S2ともに,領域?で発生させた場合,水面波の波長は 2.0cmであった. A 波源S1がx軸上を正の向きに速さ1.0cm/sの等速で動く場合を考える. 波源は原点Oを出発した時刻t=0[s]に振動を開始し,領域?に達する直前 に振動を停止させる. (1)波源S1から出た波が,(16,0)に達してからこの点を通過し終わるのに 何秒かかるか. (2)波源S1から出た波が領域?をすべて通過し終わる時刻はいつか. B 次に波源S1を原点Oに固定し,もうひとつの波源S2をx軸上に置いて, 同位相で振動させる. (3)波源S2を(16,0)からゆっくりとx軸正方向に移動するとき,波源S1S2間 に初めて定常波が生じるのはどこか.x座標で答えよ. (答え)(1)8.0秒(2)22秒(3)17.25 長々と書いてごめんなさい.どなたかご教授のほどよろしくお願いします.
Re: 愚問ですみません.
yama さんのレス (2006/08/01(Tue) 23:20)
疑問点は何でしょうか. 問題の丸投げには答えかねますので,自分でどのように考え,どこに疑問を持ったかを書いてください.
Re: 愚問ですみません.
mNeji さんのレス (2006/08/02(Wed) 09:15)
はじめまして.
とても複雑な問題の割には,y軸方向の設定が不明です.これは致命的な出題ミスとも思えます.
この問題は,どんな学校・学年・講義での出題でしょうか?ひょっとして,語学の翻訳問題とか?
また,長文を書くなら,段落は付けて書かないといけませんね.
Re: 愚問ですみません.
歩き目です さんのレス (2006/08/02(Wed) 21:22)
yamaさんへ すみません.はじめは,疑問点を書こうと思ったのですが,それを書くと ものすごい行数になってしまうので,あえて省きました. でも,ご指摘の通り書こうと思います. テストの解説では, (1)最後の波-はじめの波=16-8=8.0秒 (2)最後の波が点Qを通過…16秒 ?を通過…6秒∴22秒 (3)解説なしといった感じだったのですが,疑問点としてははじめの波, 最後の波って何ですか?もう訳がわかりません.波は連続して伝わってい くのだからはじめと終わりという表現は変じゃないでしょうか? まだ,自分が波というものを十分理解してないからかもしれませんが…. よろしくご教授のほどお願いします.
mNejiさんへ 見づらくなってしまいすみませんでした.ただ段落などの点については, うちの物理教師に言っていただきたい. なお,この問題は某公立高校の3年の実力テストです. y軸方向の設定が不明ということですが,そちらの方も物理教師に言って いただきたいです.僕はただ問題文を丸写ししただけですので….
Re: 愚問ですみません.
yama さんのレス (2006/08/02(Wed) 22:11)
はじめの波とは,波源が振動を始めたときに発生した波です. 最後の波とは,波源が振動を停止する直前に発生した波です.
とはいっても「はじめの波」や「最後の波」という言葉が適切かどうかは疑問ですね. 「波束の先端」「波束の後端」というほうがいいような気がします.
Re: 愚問ですみません.
mNeji さんのレス (2006/08/02(Wed) 22:25)
もし,本当にお書きになった文章が完全であるならば,この教師の適正が疑われます.私は,市民の一人としてこの高校に抗議の用意があります.
私のメール先は,このサイトの私のページに書いてありますので,メールください.
念の為に,確認しますが,出題の中に,「y方向は無限に続く」とか「y方向からの反射は無いものとする」とかの記述は無いのですね?
お早いご返事ありがとうございます.
歩き目です さんのレス (2006/08/02(Wed) 23:01)
はい.多分反射は考えずに屈折だけでやれということなのだと思います. ところで,本当に自分の愚かさに呆れてしまうのですが,率直に言って何が わからないのかわからない状態です.もしよろしければ一通り解説をしてい ただけないでしょうか?そうすればその解説を見て僕の疑問点が判明するか もしれませんので.申し訳ありませんが,自分で疑問点を明らかにして返答 を返すのは無理です.本当にすみません.
Re: お早いご返事ありがとうございます.
yama さんのレス (2006/08/03(Thu) 13:01)
mNejiさんの指摘のようにこの問題にはかなりの不備があるので,何がわからないのかわからないというのも無理もないような気がします.
まず水槽の内壁による波の反射が問題です.これがあると,状況が複雑になるので,内壁は波を反射させないような特殊なしくみになっているか,または水槽が考えている領域に比べて十分広く,考えている時間内には反射波が返ってこないと考えないといけません. しかし問題文にはそのような説明はありません.少なくとも「水槽内壁による反射波は考えないものとする」というような但し書きが必要だと思います.
次に,領域?,?のy方向の幅が与えられていないのも問題です. y方向の幅が広いほど,通過するのに時間がかかるはずですが,幅がわからなければ,その時間を求めることはできません. ところが,解答を見るとy方向の幅は無視されているようですね.つまり,領域のy方向の幅は十分狭いものとして,x方向の運動だけを考えているようです. そうだとすると,「領域の幅は波長に比べて十分狭いものとする」というような但し書きが必要ですね. この場合は,波の屈折を考える必要はなく,領域?,?での波の速さを求めれば,簡単な計算で通過時間が求められ,解答と一致することがわかるでしょう.
次にBの方ですが,これもいろいろな問題があります. S1とS2で発生した波の干渉によって定常波ができるという設定のようですが,実際には定常波はできません. 定常波ができるためには,同じ振幅と振動数を持ち,互いに逆向きに進む波が干渉する必要があります.ところが1点から円形に広がる波は,広がるにつれて振幅が減少していきます.そのためSIS2間全体で2つの波が同じ振幅で重なることはないので,定常波はできません. ところが,円形波について「振幅は変化しないものとする」というような非現実的な設定をした問題はよくあります.そのように設定すれば確かにS1S2間に定常波ができることになりますが・・・. もう少し現実的な設定としては水槽の幅を十分狭くすることです.つまり狭い溝状の水槽を考えるわけです.その場合は振幅がほとんど変化しないので定常波ができることになります. それはともかく,定常波ができるとしても,解答の17.25という数値がどうして出てくるのか不明です. 弦や気柱の振動で定常波ができる場合は,端が腹になるとか節になるとかの条件を満たさないといけません. しかしこの問題の場合は,S1やS2が腹や節である必要はないので,S2の位置に関わらず定常波ができるはずです.
さらに非現実的な設定も気になります.振動数と波長から計算すると,領域?での波の速さは2.0cm/sという小さい値になります. 水深によって波の速さが異なることから重力のはたらきによる波と考えられるので,速さから水深を計算すると0.004cm程度になります.これで水槽といえるかどうかはともかくとしても,この場合は,表面張力による波も無視できないでしょう. また,波源が振幅0.50cmで振動するということですが,それによって生じる波の振幅はどうなるのでしょうか?水深0.004cmのところで振幅0.50cmの波が発生するのでしょうか? もっともこの問題では振幅の値自体は解答に関係しないようですが・・・.
このようにいろいろな不備や疑問点があります. この掲示板でのやりとりをプリントアウトして先生に見ていただいたらいかがでしょうか?
Re: お早いご返事ありがとうございます.
歩き目です さんのレス (2006/08/03(Thu) 20:53)
17.25の件ですが講評というのを見てみると, (18.5-16)÷2=1.25 1.25+16=17.25だそうです. 相変わらず他の問いに関しては,前の書き込みで示した説明があるだけでした. あと,yamaさんの提案ですが,残念ながらそれは無理なんです. 僕が教わっている(そしてこの問題を作った)先生は一度定年退職されて, 再任された先生なので,自分の授業が終わるとさっさと帰ってしまうのです. 僕がここで,皆さんに助けを求めているのはそういう事情からなんです. mNejiさん,yamaさんの指摘された出題ミスはすべて大目(?)にみてこの問題 を解説していただくことはできないでしょうか?何卒よろしくお願いします.
Re: お早いご返事ありがとうございます.
mNeji さんのレス (2006/08/03(Thu) 22:35)
私も,yamaさんがご説明されているように,この問題はあまりにも多くの矛盾が多すぎて,高校生の皆さんが解くことによって物理の理解が深まる問題とは思えません.
百歩譲って,勉強したければ,適切な参考書を購入されることをお勧めします.もし,どんな本が良いか知りたければ,ここで質問されれば,多くの先輩が助言くださると思います.
他方,テストで成績に関わるので,ということならば,それこそ,このスレッドの印刷をもって,学年主任の先生,教頭先生,校長先生,場合によっては教育委員会にたいして申し入れをする必要があると思います.
少なくとも,ご両親とか担任の先生に,この事情は話されてみたら如何ですか?公開の場所では言いにくければ,物理かぎしっぽプロジェクト・メンバーのなかで相談し易そうな人にメールでお聞きになるのも一法ではないでしょうか?
モヤモヤ感が残りますが
歩き目です さんのレス (2006/08/03(Thu) 22:58)
なんだかすっきりしないのですが,皆さんの手を煩わせてしまい すみませんでした.これからもお世話になるかと思いますがよろ しくお願いします.
Re: モヤモヤ感が残りますが
CO さんのレス (2006/08/04(Fri) 02:26)
CO です.
とりあえずこのまま終わってはもったいない(教育的ではない)ので,以下のような問題に改変して解いてもらってはどうでしょうか. これが解ければ,この問題が何をやらせたかったのか分かると思います. (問題に不備があればお知らせください.領域 II はわざと改変しました)
# 私は,このままだと簡単すぎると考えた先生が状況を<b>無理に</b>複雑にしたのではないかと思います..
一次元の波動を考える.
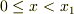 の範囲を領域 I ,
の範囲を領域 I , 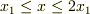 を領域 II とする.
領域 II での波の伝わる速さは 領域 I での
を領域 II とする.
領域 II での波の伝わる速さは 領域 I での 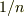 倍である.
倍である.
いま二つの波源 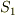 ,
, 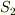 がある.
どちらも同じ振幅をもち,振動数
がある.
どちらも同じ振幅をもち,振動数  で振動して波を作り出す.
波源
で振動して波を作り出す.
波源 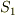 ,
, 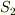 ともに,領域 I で波を発生させた場合に波の波長は
ともに,領域 I で波を発生させた場合に波の波長は 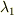 であった.
ただし
であった.
ただし 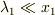 である.
である.
<b>A.</b>
波源 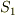 が
が  軸上を正の向きに速さ
軸上を正の向きに速さ  の等速で動く場合を考える.
ただし
の等速で動く場合を考える.
ただし  は領域 I における波の伝わる速さより遅い.
波源
は領域 I における波の伝わる速さより遅い.
波源 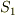 は原点
は原点 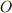 を出発した時刻
を出発した時刻 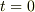 に振動を開始し,領域 II に達する直前に振動を停止させる.
に振動を開始し,領域 II に達する直前に振動を停止させる.
- 波源
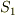 から出た波が最初に
から出た波が最初に 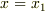 に達してから,この点を通過し終わるまでにどれだけの時間がかかるか.
に達してから,この点を通過し終わるまでにどれだけの時間がかかるか. - 波源
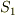 から出た波が領域 II を全て通過し終わる時刻はいつか.
から出た波が領域 II を全て通過し終わる時刻はいつか.
<b>B.</b>
次に波源 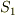 を原点
を原点 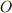 に固定し,もう一つの波源
に固定し,もう一つの波源 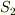 を
を  軸上に置いて,同位相で振動させる.
軸上に置いて,同位相で振動させる.
<s>
(3) 波源 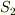 を
を 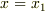 からゆっくりと
からゆっくりと  軸正方向に移動するとき,波源
軸正方向に移動するとき,波源 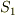 ,
, 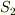 を腹とする定常波が初めて生じる位置はどこか.
なお,
を腹とする定常波が初めて生じる位置はどこか.
なお, 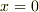 ,
, 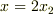 では自由端反射をするものとする.
</s>
では自由端反射をするものとする.
</s>
Re: モヤモヤ感が残りますが
歩き目です さんのレス (2006/08/04(Fri) 21:19)
どう考えればよいのかわかりません. どなたかヒントをお願いします.
Re: モヤモヤ感が残りますが
yama さんのレス (2006/08/04(Fri) 23:35)
ヒントを書いておきます.
A.
(1) まず振動数と波長から,領域 I での波の速さを求めます.
この速さを用いて,波が最初に  に達する時刻
に達する時刻 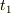 を求めます.
次に,時刻
を求めます.
次に,時刻 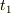 における波源
における波源 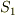 の位置
の位置 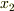 を,波源の速さを用いて求めます.
この時刻
を,波源の速さを用いて求めます.
この時刻 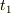 に波の発生が停止するので,この直前に発生した波が
に波の発生が停止するので,この直前に発生した波が 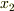 から
から 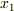 に伝わる時間
に伝わる時間  を求めればいいわけです.
を求めればいいわけです.
 に波束の後端が達する時刻は
に波束の後端が達する時刻は 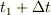 なので,これに,波が領域?を通過するのに要する時間を加えたものが求める時刻になります.
なので,これに,波が領域?を通過するのに要する時間を加えたものが求める時刻になります.
Re: モヤモヤ感が残りますが
歩き目です さんのレス (2006/08/05(Sat) 01:20)
yamaさんの助けを借りてなんとかやってみました.どうでしょうか? (1)X1(1/v-1/fλ) (2)X1/v+nX1/fλ
Re: モヤモヤ感が残りますが
yama さんのレス (2006/08/05(Sat) 11:12)
残念ながら違っているようです. たとえば特別な場合として,v=0,すなわち波源が動かない場合を考えると(1)の解が x1/fλ1 になることが容易に分かると思います.しかし,あなたの解で v=0 とおいても x1/fλ1 にはなりません. このように特別な場合を考えて,解答をチェックしてみることも大切です.
Re: モヤモヤ感が残りますが
歩き目です さんのレス (2006/08/05(Sat) 14:37)
波源S1は領域?に達する直前に波の発生を停止するのであって, 時刻t1に停止するのではないと思います.
Re: モヤモヤ感が残りますが
yama さんのレス (2006/08/05(Sat) 14:46)
波の先端が領域?に達する時刻をt1としたので,波源の振動が停止するのは,時刻t1の直前ですね.時刻t1の直前ということは,時刻t1に限りなく近い時刻なので,ほとんどt1と考えていいと思います.
Re: モヤモヤ感が残りますが
歩き目です さんのレス (2006/08/06(Sun) 20:57)
give upです. もうわけがわかりません.
Re: モヤモヤ感が残りますが
yama さんのレス (2006/08/07(Mon) 13:13)
ヒントに従って考えればできます.
A.
(1) まず振動数と波長から,領域 I での波の速さを求めます.
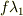 になりますね.
この速さを用いて,波が最初に
になりますね.
この速さを用いて,波が最初に  に達する時刻
に達する時刻 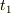 を求めます.
を求めます.
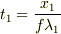 となります.
次に,時刻
となります.
次に,時刻 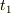 における波源
における波源 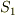 の位置
の位置 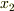 を,波源の速さを用いて求めます.
を,波源の速さを用いて求めます.
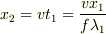 となります.
この時刻
となります.
この時刻 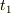 に波の発生が停止するので,この直前に発生した波が
に波の発生が停止するので,この直前に発生した波が 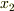 から
から 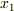 に伝わる時間
に伝わる時間  を求めればいいわけです.
を求めればいいわけです.
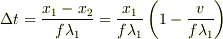 となります.
となります.
(2)  に波束の後端が達する時刻は
に波束の後端が達する時刻は 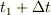 なので,これに,波が領域?を通過するのに要する時間を加えたものが求める時刻になります.
波が領域?を通過するのに要する時間は
なので,これに,波が領域?を通過するのに要する時間を加えたものが求める時刻になります.
波が領域?を通過するのに要する時間は 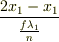 になりますね.あとの計算は分かると思います.
になりますね.あとの計算は分かると思います.
疑問点
歩き目です さんのレス (2006/08/07(Mon) 20:11)
yamaさん,ご丁寧にありがとうございます. でも,以前質問した部分がやっぱりよくわからないのです. t1はX1/fλまではわかるのですが, (波の発生が停止する時刻)=X1/vでこれはt1に等しくないので, 時刻t1に波の発生が止まることが理解できません. そして,なぜt1における波源S1の位置を求めるのかもわかりません.
※自分の解答 波が達する時刻…t1=X1/fλ 波が通過し終わる時刻…t2=X1/v ∴t2-t1=X1(1/v-1/fλ)
Re: 疑問点
CO さんのレス (2006/08/07(Mon) 20:23)
CO です.
問題文が二通りに解釈できてしまうようです..
> 波源 |9f15cdedd8d76e4abb50732f5727065b| は原点Oを出発した時刻 |1f48e973d6a9075dbaaf41a9e85f034e| に振動を開始し,領域 II に達する直前に振動を停止させる.
yama さんは「波が」領域 II に達する直前( 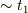 )に波源が停止すると考えておられるようです.
)に波源が停止すると考えておられるようです.
一方,歩き目です さんは「波源が」領域 II に達する直前に波源が停止すると考えておられるようです.
ですので,歩き目です さんは 歩き目です さんのやり方であっていると思います. どちらが合っていてどちらが間違っているとは言えないです.
なお,元の問題では 歩き目です さんの解釈を期待しているようです. (そうすると答えが一致するため)
Re: 疑問点
歩き目です さんのレス (2006/08/07(Mon) 20:50)
ありがとうございました. それと,COさんはなぜ(3)を削除されたのですか? どう改題しても無理な問題だったのですか?
Re: 疑問点
yama さんのレス (2006/08/07(Mon) 21:02)
なるほど,そうですね. 歩き目ですさんの答でいいと思います.
Re: 疑問点
CO さんのレス (2006/08/08(Tue) 00:49)
> それと,COさんはなぜ(3)を削除されたのですか? > どう改題しても無理な問題だったのですか?
作ろうと思えば作れますが, やっていただく価値のある問題を思いつかなかったのです.
もしチャレンジ精神がおありならば,yama さんが指摘してくださった
「 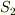 がどこにあろうと定常波ができる」
というのを説明してみると良いと思います.
(もちろん高校物理の範囲内で説明できます)
がどこにあろうと定常波ができる」
というのを説明してみると良いと思います.
(もちろん高校物理の範囲内で説明できます)