ドップラー効果の端で

サンダさんの書込 (2006/07/31(Mon) 15:13)

どうも高三理系のサンダです．波動でばかりお世話になってるような気がしますが今回も波動です．どうぞよろしく．

振動数ｆの音源が観測者に速さｖで近付いてくる場合，観測者の聞き取る音の波長λを求めよ．ただし，空気中の音速をｚとする．

という内容の問題で，解答には

「(z-v)の中にｆ個の波があるのでλ=(z-v)/f」

とのことですが，この文章の意味が何の事かわかりません．どうか解説お願い致します．

まず，自分で絵を描いて考えてください．最初の波が発生して1秒の間に何個，波が発生しますか? その間最初の波はどこまで進んでいますか，発生源はどこまで進んでいますか?

この場合，波動の周期，Tで考えた方が楽と思います．

いま観測者が，あるフェイズで，波が放出されたのを観測したとします．とうぜんそれからT後に同一のフェイズの次の波がでますがその間に，音源はv進んでいますので；

λ= z*T - v*T = (z-v)*T = (z-v)/f

上の文章と下の絵との間に，少し観点が違ってしまいましたが目をつぶってくださいね．

◎→ ↑(あるフェイズの波)が放出された位置=０

→ ↑(あるフェイズの波)が伝播された位置=z*T ◎→ ＋ ↑(次のフェイズの波)位置=v*T ＋＋ーーーーーーーλーーーーーーー＋

＃ASCIIアートは空白文字と相性が悪い．＃巧く見えなかったら，御免なさい．

返信が早くて助かります，どうも．

(z-v)は速さm/s，fは振動数1/sということで適当な時間ｔを掛けると (z-v)t→距離，ft→振動回数すると「(z-v)の中に〜の意味が通りますがそういうことでいいんでしょうか？

vの速さからzのモノを放つのだから(z+v)のようなイメージがあったんですけどもそもそも音速は変わらないんですよね．妙な勘違いでした．

>(z-v)は速さm/s，fは振動数1/sということで適当な時間ｔを掛けると (z-v)t→距離，ft→振動回数すると

「fは振動数1/s」というのは，1秒間にf周期の波が発生していることです．

1つの波が作られる時間幅を「周期，Tとし，その単位はs」とは習わないのですか？

従って，この場合，T＝1/fですが，ディメンションがあうからそう決めたのではありません．そんな論議ならしないほうがいいですね．

次元を気にしているのはその所為で文章がおかしくなっているからなんです．

「（速さ）の中に（振動数）個の波があるから〜だとどうも釈然としないのは間違っていますか?

> 「（速さ）の中に（振動数）個の波があるから〜だと > どうも釈然としないのは間違っていますか?

(z-v) もも次元では時間分の1がかかっています．

だから元の文は「(z-v)(*単位時間)の中にｆ(*単位時間)個の波があるのでλ=(z-v)/f」と1単位時間が暗黙のうちにかかっていると考えるか，

mNejiさんの助言のように，1周期( 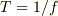T=1/f )後の変化を考えて「(z-v)*T(=(z-v)/f)の中にf*T(=1)個の波があるのでλ=(z-v)/f」と考えればいいのでは?