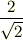放物線型偏微分方程式
放物線型偏微分方程式
土木4年 さんの書込 (2006/07/24(Mon) 02:42)
次の境界条件の偏微分方程式の方程式の解法を どなたかご存知ありませんか? 流体力学で,ナビエ・ストークス方程式の厳密解が求まる例, レーリーの問題として紹介されているのですが, たいてい,解法が省略してあります.. 自分は大学4年です. 気になったので,聞いてみました.
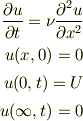
ちなみに  は,動粘性係数です.
は,動粘性係数です.
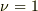 として示して下さってもかまわないです.
として示して下さってもかまわないです.
どうしても僕の力と手持ちの資料では 以下のような解を示せません.
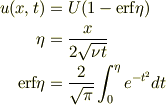
Re: 放物線型偏微分方程式
mNeji さんのレス (2006/07/24(Mon) 04:01)
寝るところなのですが,興味があるので逆質問させてください.
私も,流体力学に接近中なのですが,いまは複素関数の正則性でトラぶっています(笑).もし良かったら,その本を教えてくださいますか?
とりあえず,数学の問題とみれば,
一次元の拡散方程式みたいですね:左辺は時間について1次の偏微分だけですよね?
- 初期条件:u(t,x)=0 (t <= 0) → 初めには流れが存在しない
- 境界条件:u(0,t) = U =一定? → 原点から常時一定流が発生
- 境界条件:u(∞,t) =0 → 十分遠方では,流れは減衰して消滅.
と考えて良いですか?
# 直ぐには解けないですが,ゆっくりなら可能だろうとおもいます. # 急ぐのなら,他の方へにヘルプをお願いください.
Re: 放物線型偏微分方程式
mNeji さんのレス (2006/07/24(Mon) 14:53)
ご質問を纏めると
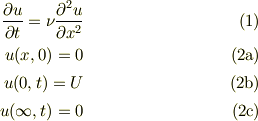
を偏微分方程式問題として解くことによって,下記の解を得たい.と言うことだとおもいます.
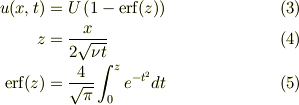
この式は,t=0で急に爆発したハワイ諸島の火山から,比較的さらさらした溶岩が流れだす場合の解析と言う感触でしょうね.
さて,この手の偏微分方程式の常法の一つには,変数変換を用いて常微分方程式に持ち込むことが予測されます.波動型の場合,(x,t) → z=x+-ct などが有名ですね.
わたしは,拡散型の変換を良く知らないので,ここではインチキして(4)を用いて考えてみます.
そこで,新しい関数;

右辺の偏微分は,左辺の全微分*zの偏微分となります.
その為には(4)より
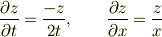
に注意して,実際に,ゴニョゴニョ(この詳細は;2006/07/25(Tue) 01:16 No.10917にメモあり)すると
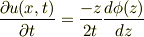
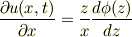
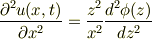
これを基の(1)に代入すると
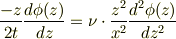
なにやら難しげですが,(4)により整理すると
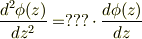
とおお化けします. 「???」に正しい値をもってこれれば,この微分方程式は変数分離ができそうです.
ここまでを解いて見てください.
正解は; 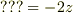 です.
です.
偏微分方程式(1)が,常微分方程式に変換できました.
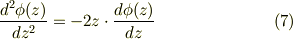
この式を良く見ると,変数分離形式であるのが判ります;

Re: 放物線型偏微分方程式
土木4年 さんのレス (2006/07/25(Tue) 00:07)
mNejiさんの教えていただいたように, 無事導けました.
ちなみにこの問題は, 岩波新書物理テキストシリーズ9今井功流体力学 の第8章§46一方向流れ192ページです. この教科書では,この方程式は,一方向流れを仮定し, 圧力勾配が存在しないとき, 平板を一方向にt>0でUの速度で動かしたときのナビエストークス方程式 となってます.
ただ計算途中気になったのが,
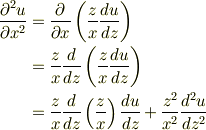
となって,第一項が余分に出てくるのでは?と思いましたが, 第一項を無視して計算したら,あってたので不思議です.
Re: 放物線型偏微分方程式
mNeji さんのレス (2006/07/25(Tue) 00:31)
>となって,第一項が余分に出てくるのでは?と思いましたが, >第一項を無視して計算したら,あってたので不思議です.
書くのを省略しました.見てくれを良くなるようにしました.z/xはtだけの関数なので,xの偏微分に関係しないのです....
折角ですから,積分して境界条件をつけるところまで書いて見ては如何ですか? TeXの練習にもなりますし,他の方の参考にもなると思います.
#私が簡単に出したところ,erfの係数が違ってました.
#erfを無限大まで積分した値を 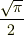 としたのが間違いですかね?
としたのが間違いですかね?
>岩波新書物理テキストシリーズ9今井功流体力学 >の第8章§46一方向流れ192ページです.
情報感謝します.「岩波新書」とは知りませんでした.拝見してみます.
Re: 放物線型偏微分方程式
土木4年 さんのレス (2006/07/25(Tue) 00:47)
一応,自己解決しました. 変数変換を
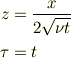
と考えれば, 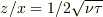 なんで,これをzで偏微分しても0になります.
なんで,これをzで偏微分しても0になります.
ただ
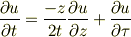
でおつりがでてきます.
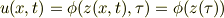
で時間に陽に依存してなければ,おつりは0だからよさそうです. 若干いい加減な気もしますが.
Re: 放物線型偏微分方程式
mNeji さんのレス (2006/07/25(Tue) 01:16)
>あと岩波"書店"でした.
了解.
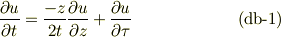
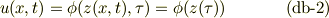
上記の解釈は,極端に間違っています.
==============================
自分の式も微分のdが抜けていたので下記に訂正します.
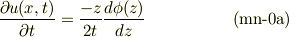
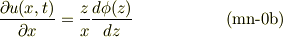
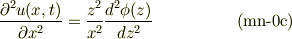
==============================
ここでは,偏微分方程式の解 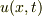 を常微分方程式の解
を常微分方程式の解 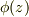 に変換する操作を考えます.
に変換する操作を考えます.


左辺の関数uは,独立変数,xとyとの陽の関数です.敢えて言えば,zの関数と考えません.
他方,右辺にはxやtは陽に入っていないのが味噌です.これらは関数 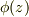 はzの陽の関数であっても,xとyとの陽の関数ではなく,敢えて言えばxとyとの陰関数です.
はzの陽の関数であっても,xとyとの陽の関数ではなく,敢えて言えばxとyとの陰関数です.
勿論,関数zを考えると,zはxとyとの陽の関数です.
ですから,上式の全微分を考えると;
左辺の全微分: 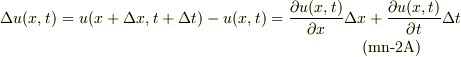
右辺の全微分: 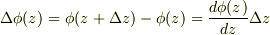 ここで
ここで 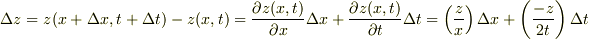
最終的に,右辺の全微分: 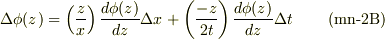
u(x,t)の偏微分を考える時は,(mn-2A),(mn-2B)式の 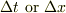 の係数同士を等しいとすればよい.
の係数同士を等しいとすればよい.
念のために,個別に比較する:
 の係数を比較して;
の係数を比較して;
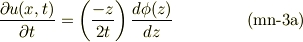
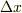 の係数を比較して;
の係数を比較して;
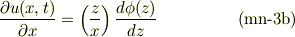
上式で, 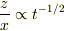 で,xの偏微分に関与しないことから,
で,xの偏微分に関与しないことから,
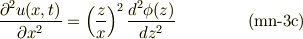
注意していただきたいのは,左辺の被・偏微分関数は 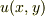 であり,右辺の被・微分関数は
であり,右辺の被・微分関数は 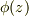 だけだと言うことです.
だけだと言うことです.
導出修正
土木4年 さんのレス (2006/07/25(Tue) 02:32)
導出してみました.
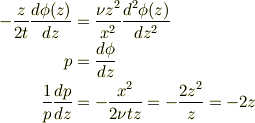
ここで両辺  で積分
で積分
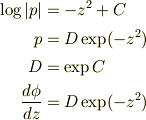
両辺を  で
で 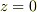 から
から 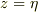 で積分
で積分
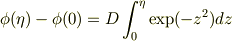
境界条件より
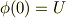
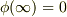 より
より
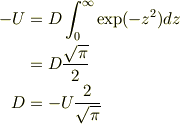
>z/xはtだけの関数なので,xの偏微分に関係しないのです....
z/xをxで偏微分して0になるのは確かですが, zで常微分しても0になるかわからないじゃないですか... ...と思いましたが,
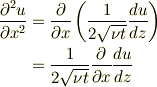
ってことですね. 納得しました.ありがとうございます. 説明してくださるなら,していただきたいですが.
あとパスワード設定してなかったので,修正できませんでした.すいません.