1年 さんの書込 (2006/07/23(Sun) 18:36)

問題解いていただけませんか？どなたかお願いします．

（１） 光速の0.99倍で運動している粒子の寿命は静止しているときの何倍になるか？ （２） 光速の0.999倍で走っている全長50mの宇宙船の中央から出た光が最後端と最先端に達する時の時間差は静止系からながめたとき何秒になるか？

（３） ある物体の長さが進行方向に60%だけ収縮してみえた．この物体の速さを計算せよ． （４） 全長500mの列車がある観測者に対して，0.6cの速さで走っている観測者は，この列車の長さLを何mと観測するか？

（５） 光速0.8倍の速さで走っているロケットから光速の0.7倍の速さの粒子を発射した．粒子の合成速度を求めよ． （６） 赤方編数の式においてv/cの値を変化させるときν_r/ν_0がどのように変化するか調べよ．

（７） 全エネルギーが50Gevに加速された陽子の質量は，静止質量の何倍か？そのときの陽子の運動量と速さはいくらか？

mNeji さんのレス (2006/07/24(Mon) 00:21)

「120％わかる相対論」なんていう感じの本を見てくれば良いのでは？

Joh さんのレス (2006/07/24(Mon) 00:39)

＞問題解いていただけませんか？どなたかお願いします．

人にものを頼むときには，きちんと礼儀正しく頼んでください．

1年 さんのレス (2006/07/24(Mon) 02:20)

お分かりになる方がいらっしゃれば，お教えください．おねがいします．

土木4年 さんのレス (2006/07/24(Mon) 02:52)

とりあえず(1)と(3)だけ， (1)

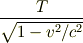
に 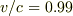代入． (3)ローレンツ収縮

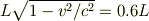
を解けばよいと思います．

あと(4)の問題の意味があいまいだと思います． どっちが0.6cで走っているのかわかりません．

扉 さんのレス (2006/07/24(Mon) 03:46)

土木4年さんの言うとおり4はあいまいでよく分かりません．しかし相対速度なので計算上問題はないんですけどね，（苦笑い） 4の問題は x'＝γ（x−vt）・・・?※γ＝1/√（1−（v/c）^2） なので電車から見た長さはL'＝x'−x．'ですよね？ この式に?をx'とx．'の両方に代入すると，簡単な計算ののちに， L'＝γ（x−x．）＝γLになります．（vtは相殺した）つまり L＝1/γL'に代入すれば求まりますけど，他の問題もちょっとした基本が分かっていれば人に聞かなくても解くのは簡単なので基本をまずは理解したほうがいいと思いますよ☆