行列の対角化

home > 掲示板 >

このページのPDF版

サイトマップ

行列の対角化

２年生さんの書込 (2006/07/22(Sat) 18:19)

こんにちは．対角化の問題なのですが，手持ちの参考書をみると 1，行列Aの固有値と固有ベクトルを求める． 2，変換の行列候補Pを固有ベクトルを並べて作る． 3，Pの行列式の値が0にならないことを確認し，固有ベクトルが線形独立であることを確認． 4，Pと対角化された行列を求める．となっているのですが，固有ベクトルは，固有空間の基底になっているわけですよね？それならば線形独立になっていることは自明(基底は線形独立なベクトル)なので，n次元の行列に対してn個の固有ベクトルを見つけることだけ確認すれば上記の「3」の手続きは必要ないのではないでしょうか？

Re: 行列の対角化

mNeji さんのレス (2006/07/22(Sat) 19:16)

固有値が重根を持つ(縮退とも言う筈)場合は？

Re: 行列の対角化

２年生さんのレス (2006/07/22(Sat) 19:38)

重根を持つ場合は，重根の固有値の固有空間から基底を必要な分だけ取り出せばいいのではないでしょうか？その基底は必ず線形独立ですよね．

Re: 行列の対角化

toorisugari no Hiro さんのレス (2006/07/22(Sat) 19:48)

> n次元の行列に対してn個の固有ベクトルを見つけること 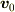$\bm{v}_0$ が固有ベクトルであれば 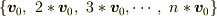$\{\bm{v}_0,~2*\bm{v}_0,~3*\bm{v}_0,\cdots,~n*\bm{v}_0\}$ も条件をみたしますよね．つまり，独立な組を選ぶと言う文言をどこかに入れなければいけないと言うだけでは?

Re: 行列の対角化

mNeji さんのレス (2006/07/22(Sat) 20:31)

>重根を持つ場合は，重根の固有値の固有空間から基底を必要な分だけ取り出せばいいのではないでしょうか？ >その基底は必ず線形独立ですよね．

これから先は，手持ちに参考書がないので自信が無いのですが，行列Aを幾らにらんでいても，縮退した基底を解けないですよね．どうやるのでしたか？

Re: 行列の対角化

２年生さんのレス (2006/07/22(Sat) 21:19)

＞toorisugari no Hiroさんということは上記のように行列式の値を調べなくても一言，「これらの固有ベクトルは線形独立である」とでも表記しておけば，解答にバツされることはないでしょうか？

＞mNejiさん

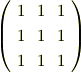
$\left(\begin{array}{ccc}1 &1 &1 \\1&1 &1 \\1&1 &1 \end{array}\right)$

という行列の固有値は3と0で，0は重複度2なのですが，λ=0のときの任意のxは

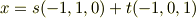
x=s(-1,1,0)+t(-1,0,1)

と表すことができて，基底を２つ取り出すことができます．λ=3のときは当然，基底が１つ取り出せるので，３次元の行列に対して３つの線形独立な固有ベクトルが取り出せるので，対角化可能．という解答では駄目なのか？と思ったのです．もちろん，重複度ぶんだけ固有ベクトルが取り出すことができない場合もありますが，それはｎ次元のベクトルに対して〜個の固有ベクトルしか取り出せないので対角化不可能とでも書いておけばよいのではないでしょうか？

Re: 行列の対角化

Chappy さんのレス (2006/07/22(Sat) 21:36)

こんにちは，２年生さん．Chappyというものです．

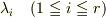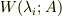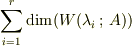ｎ次正方行列Ａを対角化しようと考えるときに， ?固有値と固有ベクトルを求めて，(今，固有値がｒ個あるとします) ?各固有値 $\lambda_i\quad(1\leqq i\leqq r)$ に対応する固有空間 $W(\lambda_i;A)$ の次元の和 $\sum_{i=1}^r \dim(W(\lambda_i\,;\,A))$ がｎだったら，対角化できますよ．それが必要十分条件です．また，固有ベクトルたちは１次独立になります．

＃(先ほどの発言は取り下げました)

Re: 行列の対角化

２年生さんのレス (2006/07/22(Sat) 22:14)

こんにちは．はい，教科書にはその定理が書いてありました．しかし，次元というのは，基底の数のことでしたよね？解答するときは固有空間の基底を固有ベクトルとして選びます．

ということは，Chappyさんのおっしゃる定理は，単に固有ベクトルの数がｎ個あればいいということと同じで，解答するときはわざわざ定理を書かなくても，単に自分の求めた基底(固有ベクトル)の数を数えればいいのではないでしょうか？

Re: 行列の対角化

Chappy さんのレス (2006/07/22(Sat) 22:37)

はい，その通りです．だから，

>Pの行列式の値が0にならないことを確認し，固有ベクトルが線形独立であることを確認．

というのは，わけが分かりません．．．Ｐの行列式が０にならないことを確認しなくても，固有ベクトルは線形独立ですから．．．． (僕が書いた上の定理の内容で)ｎ個の固有ベクトルが取れないときはＰ自体考えられないのではないかと思ってしまうしだいです．

授業で習った定理を使うなってことはないでしょう．ただし，授業でその定理を習ってないなら，注意が必要かもしれません．そのときは，不本意ながら，Ｐの行列式を求めなければならないかもしれません．

Re: 行列の対角化

mNeji さんのレス (2006/07/22(Sat) 22:59)

議論は収束したようなので，質問させてください．

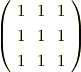
$\left(\begin{array}{ccc}1 &1 &1 \\ 1 &1 &1 \\1 &1 &1 \end{array}\right)$

の場合で良いのですが，固有値0の時の固有ベクトルの求め方はどうしてますか．それと固有値3の場合に求められている固有ベクトルとの直交性が自動的に補償されますか？

勿論，3x3は目で見れば判る世界ですが，いま論議されているのは，nxn行列ですよね？

話がおかしければ，放置しておいてください．

Re: 行列の対角化

Chappy さんのレス (2006/07/22(Sat) 23:06)

ごめんなさい，ちょろっと言ってしまった，直交性は僕の勘違いでした．最初，対称行列の対角かと勘違いしたので．

固有ベクトルの求め方を，今，ＴｅＸで打ってます．なにぶん，入力の遅い奴なので，しばらくお待ちくださいませ．

Re: 行列の対角化

２年生さんのレス (2006/07/22(Sat) 23:18)

＞Chappyさんやはり必要ありませんでしたか．よかったです．その方法は参考書に書いてあったのですが，基礎レベルの参考書なので「ちゃんと行列式の値を調べると0にはならないよ．だからちゃんと線形独立になっているよ」みたいな意図があったのかもしれません． Chappyさんのお書きになった定理ですが，教科書だとn-rank(A-λE)で計算して出しているのですが，基底の数を数えて次元を求めても間違いではありませんよね？

Re: 行列の対角化

Chappy さんのレス (2006/07/22(Sat) 23:27)

>mNejiさん入力中です．．．すみません．線形代数のよい復習になってます．

>２年生さんもちろん間違いではありません．ただし，基底を求めるステップをちゃんとすればの話です．以下，出力予定，，，，

Re: 行列の対角化

Chappy さんのレス (2006/07/22(Sat) 23:45)

途中経過，，，詳しく書きすぎたのがよろしくないのか．．．数式の上をマウスオーバーすると，大量の数式がポップアップするので注意です．僕は少し酔いました (^^; mNejiさんはfirefoxだから大丈夫でしょう．僕もfirefoxですが， ALTがポップアップする拡張を導入してます，まぁ，余談です．

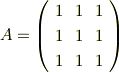
$A=\left(\begin{array}{ccc}1 &1 &1 \\ 1&1 &1 \\ 1&1 &1 \end{array}\right)$

の対角化を求めるプロセスで，固有多項式は

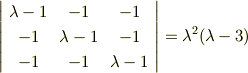
$\left|\begin{array}{ccc}\lambda -1 &-1 &-1 \\-1&\lambda -1 &-1 \\-1&-1 &\lambda -1 \end{array}\right|=\lambda^2(\lambda-3)$

で，λ＝０のとき，

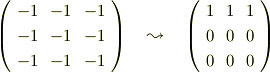
$\left(\begin{array}{ccc}-1 &-1 &-1 \\-1&-1 &-1 \\-1&-1 &-1\end{array}\right)\quad\leadsto\quad\left(\begin{array}{ccc}1 &1 &1 \\0&0 &0 \\ 0&0 &0 \end{array}\right)$

から，

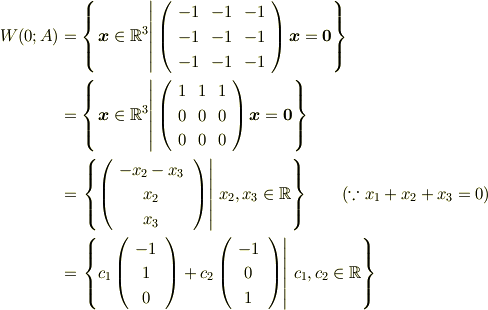
$W(0;A)&=\left\{\left.\vphantom{\begin{array}{ccc}1 &1 &1 \\1&1 &1 \\1&1 &1\end{array}}\boldsymbol{x}\in\mathbb{R}^3\right|\left(\begin{array}{ccc}-1 &-1 &-1 \\-1&-1 &-1 \\-1&-1 &-1\end{array}\right)\boldsymbol{x}=\boldsymbol{0}\right\} \\&=\left\{\left.\vphantom{\begin{array}{ccc}1 &1 &1 \\0&0 &0 \\0&0 &0\end{array}}\boldsymbol{x}\in\mathbb{R}^3\right|\left(\begin{array}{ccc}1 &1 &1 \\0&0 &0 \\0&0 &0\end{array}\right)\boldsymbol{x}=\boldsymbol{0}\right\} \\&=\left.\left\{\left(\begin{array}{c}-x_2-x_3 \\x_2 \\x_3 \\\end{array}\,\right)\right|\,x_2,x_3\in\mathbb{R}\right\}\qquad(\because x_1+x_2+x_3=0) \\&=\left.\left\{c_1\left(\begin{array}{c}-1 \\1 \\0 \\\end{array}\,\right)+c_2\left(\begin{array}{c}-1 \\0 \\1 \\\end{array}\,\right)\right|\,c_1,c_2\in\mathbb{R}\right\}$

Re: 行列の対角化

２年生さんのレス (2006/07/23(Sun) 00:14)

ご解答ありがとうございました．

＞追記：これは対角化できない例ですよね？計算間違ったかな．．．それであっています．固有値は3の場合もあるので，固有値0のときの基底２つと合わせて，３つです．だから対角化できます．

Re: 行列の対角化

Chappy さんのレス (2006/07/23(Sun) 00:21)

いや，すみません．．対角化できました．計算間違いしてました．λ＝０のほうは間違ってません．

Re: 行列の対角化

Chappy さんのレス (2006/07/23(Sun) 00:27)

参考のために，軽く書いておきます．

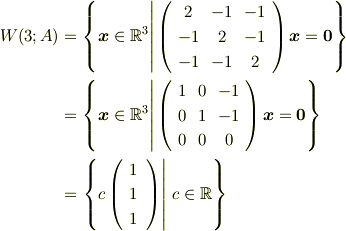
$W(3;A)&=\left\{\left.\vphantom{\begin{array}{ccc}2 &1 &1 \\1&2 &1 \\1&1 &2\end{array}}\boldsymbol{x}\in\mathbb{R}^3\right|\left(\begin{array}{ccc}2 &-1 &-1 \\-1&2 &-1 \\-1&-1 &2\end{array}\right)\boldsymbol{x}=\boldsymbol{0}\right\} \\&=\left\{\left.\vphantom{\begin{array}{ccc}1 &0 &-1 \\0&1 &-1 \\0&0 &0\end{array}}\boldsymbol{x}\in\mathbb{R}^3\right|\left(\begin{array}{ccc}1 &0 &-1 \\0&1 &-1 \\0&0 &0\end{array}\right)\boldsymbol{x}=\boldsymbol{0}\right\} \\&=\left.\left\{c\left(\begin{array}{c}1 \\1 \\1 \\\end{array}\,\right)\right|\,c\in\mathbb{R}\right\}$

といったところです，失礼しました．ふぅ，疲れた．．．大学生ならば，テストが近いのですかね？がんばってください :) 僕もテスト勉強せねば．．．

Re: 行列の対角化

mNeji さんのレス (2006/07/23(Sun) 00:35)

変な質問をしてしまったようで．

正直に言いますが，私は学生の頃，2x2の具体的な固有値を出すことで，n>=2はこれと同じようなもの．としていました. 理論的には，当時判った積りだったのが，今となっては？

どうせ物理では縮退していても，何らかの摂動で縮退が解けるからOKさ，という愚かな大胆さで逃げていたのです．ですが，Johさんの解説などに触れている内に，私の中の誠実な個性が頭をもたげてきて，今回の質問となってしまいました．

2X2では，λが決まると，(1,x)との内積をとりxを出せば良かったわけで．

今回の場合も，λが単根なら，(x_1,x_2,x_3)=(1,x,y)として出す．もしくはJohさんの解説にあったような部分行列式の比できまるような計算と思っていましたが，重根のときに，一定の処方箋が存在するか不思議だったのです．

ただ，Chappyさんの示された，（all -1）は判るのですが，縦に(111, 000,000)のマトリックスへの変化の意味が判りませんでした．

残念なことにこれ以上うまく質問できません．今回の私の質問は，2年生さんの質問と筋違いだと思うようになってきたので，しばし棚上げにさせてください．質問が出来るようになったら確実に，この掲示板に出します．

Re: 行列の対角化

mNeji さんのレス (2006/07/23(Sun) 00:37)

ご両人さん：

テストにベストを尽くしてください！

Re: 行列の対角化

Chappy さんのレス (2006/07/23(Sun) 00:51)

>テストにベストを尽くしてください！ mNejiさん，ありがとうございます．かくゆう，僕の計算ミスも，mNejiさんから紹介してもらった maximaで計算したことによって，気づいたわけであります．また，余談です．

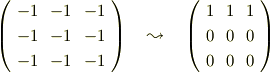
$\left(\begin{array}{ccc}-1 &-1 &-1 \\ -1&-1 &-1 \\ -1&-1 &-1 \end{array}\right)\quad\leadsto\quad\left(\begin{array}{ccc}1 &1 &1 \\ 0&0 &0 \\ 0&0 &0 \end{array}\right)$

は言葉を補わなかったのですが，行列の簡約化（基本変形をした結果）を示しています．

Re: 行列の対角化

２年生さんのレス (2006/07/23(Sun) 01:44)

テストがんばります．みなさんありがとうございました．

[home] [掲示板] [ページの先頭]