運動量保存則
運動量保存則
慎 さんの書込 (2006/07/21(Fri) 23:44)
大学1年で物理をやっているのですがよくわからない問題があるので教えてください.
ある時刻  の時のロケットの質量を
の時のロケットの質量を  ,次の
,次の  時間の間にロケットが噴射するガスの質量を
時間の間にロケットが噴射するガスの質量を 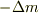 ,ロケットの速度を
,ロケットの速度を  とする.
ロケットは常にガスをロケット速度に対して相対速度
とする.
ロケットは常にガスをロケット速度に対して相対速度 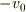 で後方に噴射する.
時刻
で後方に噴射する.
時刻 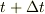 の時のロケットの速度は
の時のロケットの速度は 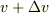 と
と 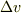 だけ加速しているとする.
ガスの速度は
だけ加速しているとする.
ガスの速度は 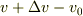 である.
この二つの時刻の間で運動量の和が等しい.
である.
この二つの時刻の間で運動量の和が等しい.
(a)時刻  の時,および
の時,および 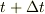 の時の運動量の和を求めよ.
(b)両者が等しいとおいて,
の時の運動量の和を求めよ.
(b)両者が等しいとおいて, 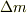 ,
, 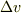 の満たす式を求めよ.
(c)
の満たす式を求めよ.
(c) 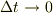 の極限をとって,上で求めた式を微分で表し,この微分の式の両辺を積分することによって
の極限をとって,上で求めた式を微分で表し,この微分の式の両辺を積分することによって  を
を  の関数として求めよ.
但し,初期条件として,
の関数として求めよ.
但し,初期条件として,  において,
において, 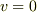 ,
, 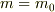 とする.
とする.
自分で解いてみると
(a)  ,
, 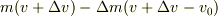 (b)
(b) 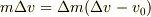 (c)
(c) 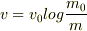 となったのですが,少し不安です.
どなたか確認していただけませんか.
となったのですが,少し不安です.
どなたか確認していただけませんか.
Re: 運動量保存則
mNeji さんのレス (2006/07/22(Sat) 02:47)
はじめまして.
> |5a72f1304af0783657605aed0e38201a| 時間の間にロケットが噴射するガスの質量を |72f374db77d6c400ecdfc6748f646bdf|
これってロケットは一定の割合で質量を減じていると考えろという事ですか?
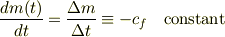
よって,
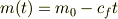
ということですか? なにか条件がいるような気もしますが.
と書きましたが,そんな条件はいらないようです.眠いので明日にします.
Re: 運動量保存則
yama さんのレス (2006/07/22(Sat) 10:33)
(3)は合っていると思いますが(1),(2)は少し違うようです.
といっても,どちらでもいいような違いですが・・・・
(a) 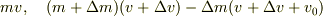 (b)
(b) 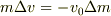 だと思います.
問題文にはっきり書いてはありませんが,相対速度
だと思います.
問題文にはっきり書いてはありませんが,相対速度 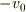 が一定ということだと思います.その場合,質量の減少の割合は一定ではないでしょうね.
が一定ということだと思います.その場合,質量の減少の割合は一定ではないでしょうね.
Re: 運動量保存則
mNeji さんのレス (2006/07/22(Sat) 12:00)
時間がないので,自分で解いた時のままを書き出します.
慣性系からみたロケットの前進速度 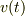 ,前進運動量は;
,前進運動量は;

慣性系からみた噴射燃料の後進速度;

(この後進速度は前進速度と同じ向きにとる:初めは負)
慣性系座標から見ると,外力は存在しないのでt とt+dtの間でのロケットと噴射燃料の運動量変化の和は零:
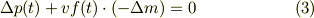
#私は,慣性系で見て, 「考えている対象の運動量の変化の総和」 = 「対象に加わる全ての外力の総和」* 「時間変化幅」
#と書き下してから具体的な計算をすすめると,どんな場合にも対応できると考えています.運動量が本質的なベクタである所以でもあります. #上の式は,「運動量の変化分は力積に等しい」とも呼ばれます. #解析力学,量子力学,電磁気学でも運動量ベクタと位置ベクタの関係は大事ですね. #以上.(追記:2006-07-23)
左辺で;
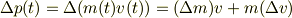
に注意して,(2)も代入して
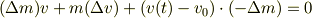
整理すると

変数分離して

積分すれば...同じみたいですね.