「コーシー・リーマンの関係式」を再考する
「コーシー・リーマンの関係式」を再考する
mNeji さんの書込 (2006/07/21(Fri) 20:11)
コーシー・リーマンの関係式については,学生時代から釈然としていなかった.これを判らないと正面切っていえなかったと思う.ですからオイラーの公式が大好きな割りに,複素関数論は弱かったのです.
今回,近くのスレッドでこの「コーシー・リーマンの関係式」を利用した計算がでてきたので,自分なりに考えてみました.いわゆる「物理屋として納得できる」かも知れませんが,数学系統のかたから見ると,「複素微分可能性」を示したことにならないとも言われそうです.
がしかし,間違いなら間違いで,ではどう考えればいいかご指導いただきたく,以下に自説を書いて見ます.数式の使い方は「現代数学への入門 複素関数論入門,神保 道夫・著,岩波書店,2003-12, ISBN4-00-006874-1」,第3章 複素数の微分と積分,p49以降にあわせています.

辺々の全微分を考えます;
左辺の全微分;
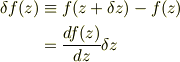
右辺の全微分
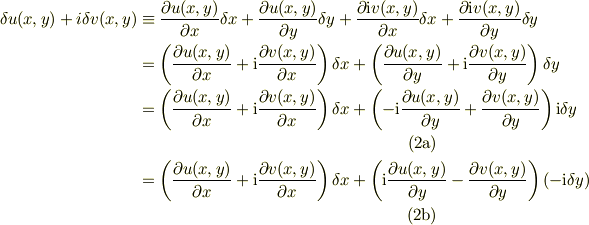
左辺の全微分が全ての方向の 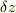 に成立するには,右辺の
に成立するには,右辺の 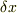 の係数と
の係数と 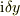 の係数とが等しく,かつ左辺の
の係数とが等しく,かつ左辺の 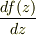 に少なくとも比例する必要がある;
に少なくとも比例する必要がある;
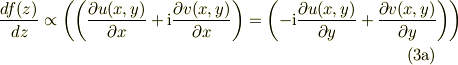
上記で関数u(x,y),v(x,y)は実数関数であるので,コーシー・リーマンの関係式が成立する.
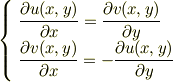
#上式の記述に当り,Chappyさんに教えていただきました.感謝します.
Re: 「コーシー・リーマンの関係式」を再考する
Chappy さんのレス (2006/07/21(Fri) 23:10)
Chappyです,失礼します... left{ 〜right.でよいと思いますよ. 記述例は以下の通りです.
![\left\{\begin{array}{@{\hskip4mm}l}\displaystyle \frac{\partial u(x,y)}{\partial x}=\frac{\partial v(x,y)}{\partial y} \\[7mm]\displaystyle \frac{\partial v(x,y)}{\partial x}=-\frac{\partial u(x,y)}{\partial y} \\\end{array}\right.](http://hooktail.maxwell.jp/bbslog/f46797fdd47deb674f81f3549e0993de.png)
left{ begin{array}{l} displaystyle frac{partial u(x,y)}{partial x}=frac{partial v(x,y)}{partial y} \ displaystyle frac{partial v(x,y)}{partial x}=-frac{partial u(x,y)}{partial y} \ end{array} right.
ソースと実際に表示される数式は少し違うように見えますが, こまごまと細かいところを修正するのは僕の悪い癖です..
Re: 「コーシー・リーマンの関係式」を再考する
mNeji さんのレス (2006/07/22(Sat) 00:13)
有難うございます.今度こそ,確実に理解できました.
>ソースと実際に表示される数式は少し違うように見えますが, >こまごまと細かいところを修正するのは僕の悪い癖です..
Tex表記は慣れるに従って,細かな制御が出来るのが嬉しいです.これからも,4649.
質問:
f(z)の全微分を考える時, 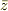 の存在も入れないといけませんか?
の存在も入れないといけませんか?
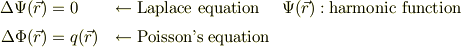
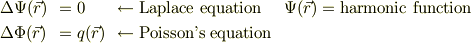
Re: 「コーシー・リーマンの関係式」を再考する
Chappy さんのレス (2006/07/22(Sat) 00:24)
は
上で微分不可能なので,
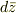 は考えられないのではないでしょうか?
は考えられないのではないでしょうか?
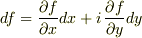 で考えてますから,
で考えてますから, 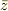 が登場する意味が分かりません...
が登場する意味が分かりません...
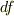 の複素共役を取る話ですかね,,,
の複素共役を取る話ですかね,,,
Re: 「コーシー・リーマンの関係式」を再考する
mNeji さんのレス (2006/07/22(Sat) 01:08)
先日COさんがご紹介された
Cauchy-Riemann Equations -- from Wolfram MathWorld
や,手元の「複素関数論入門」でも 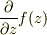 や
や 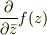 などの論議があります.
などの論議があります.
Re: 「コーシー・リーマンの関係式」を再考する
Chappy さんのレス (2006/07/22(Sat) 01:53)
すみません,理解に苦しみます... 自分の手持ちのテキスト2冊には載ってないので, 今度,解析好きの友人に聞いてみることにします.