αγ さんの書込 (2006/07/21(Fri) 04:40)

物理学の準備段階を勉強していますが， 行列の基本変形で，わからないところがあります． 「線型代数入門」（齋藤正彦，東京大学出版会）のｐ．４７，４８に 以下の記述があります．

行列の基本変形は，次の六種類の変形にほかならない． （左 １） 二つの行を入れ替える． （左 ２） ある行に０でない数をかける． （左 ３） ある行に他のある行の定数倍を加える． （右 １） 二つの列を入れ替える． （右 ２） ある列に０でない数をかける． （右 ３） ある列に他のある列の定数倍を加える．

問．（左 １）は，（左 ２），（左 ３）の組み合わせで得られることを示せ？

これが，”さっぱり”わかりません，というよりも，そ，そんな．．．． という感じですけど．どなたかお教えいただければありがたいです．

Joh さんのレス (2006/07/21(Fri) 05:18)

つるかめ算の連立方程式を解くときのイメージはありますか？

式1を二倍して，式２から引く...とか，何とかそんな操作です．

αγ さんのレス (2006/07/21(Fri) 05:27)

＞式1を二倍して，式２から引く...とか，何とかそんな操作です．

はい，それはわかります．４８ページのその問いまでは普通に理解できてますので．

列に関する，右１），右２），右３）のどれかも含めないと， 左 １）は，できないと思うのですが，何か重大な勘違いでもしてるのでしょうか？

Joh さんのレス (2006/07/21(Fri) 07:18)

列の基本変形が必要ですか？

行の基本変形だけで，対角化できますよね．そしたら，どんな行だって作れるんじゃないでしょうか？

toorisugari no Hiro さんのレス (2006/07/21(Fri) 10:13)

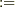えっと，すでに問題は違うところにあるようですが，とりあえず，手順をかんがえてみました．これ，プログラム中で変数 , の値を入れ替える問題と同じですね．( は代入の意味)

方法1. 一時的な変数 を用意して

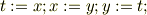
を実行する． 方法2.

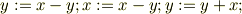
を実行する． 方法3.

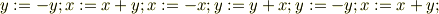
を実行する．

3が該当する手順ですね．(2は厳密には題意に則してない．) は単純な変数でなく，ベクトル(配列)でもいいので，行列の行の置換の問題も同様ですね．

ほかにもっときれいなやり方があるかもしれませんが．．．．

ｙama さんのレス (2006/07/21(Fri) 11:19)

toorisugari no Hiroさんの方法3でいいと思います． 文章で説明すると次のようになります．ただし，方法3に少し変更を加えています． 第i行xと第k行yを入れ替えるとします．ただし x,y は行ベクトルです． ?第i行に第k行の-1倍を加えると，第i行は x-y，第k行は y になる． ?第k行に第i行の1倍を加えると，第i行は x-y，第k行は x になる． ?第i行に第k行の-1倍を加えると，第i行は -y，第k行は x になる． ?第i行に-1をかけると，第i行は y，第k行は x になる． ?〜?は(左 ３)，?は(左 ２)の基本変形です．

αγ さんのレス (2006/07/21(Fri) 16:53)

おおっ，ありがとうございます．感謝です！ −１倍というのがミソだったのですね． yama さんの示された手順で 2行2列 だと，次のようになりますね．

x1 x2 x1-y1 x2-y2 x1-y1 x2-y2 -y1 -y2 y1 y2 y1 y2 → y1 y2 →x1 x2 → x1 x2 → x1 x2 //

toorisugari no Hiro さんの方法１と方法２についても， これから考えて見ます．

Joh さんご指摘： ＞行の基本変形だけで，対角化できますよね． それは知りませんでした（^-^; これから，確認します．

このサイトは，Lenstraの XTR 暗号システムを読んでて， ある用語を検索して，Joh さんの群論のご説明にたどりつきました． いやー，すばらしい説明がたくさんあって， これからしっかり勉強させていただこうと思っています． 感激です．

αγ さんのレス (2006/07/21(Fri) 16:58)

失礼しました．

x1 x2 y1 y2

x1-y1 x2-y2 y1 y2

x1-y1 x2-y2 x1 x2

-y1 -y2 x1 x2

y1 y2 x1 x2 //