即日回答お願いします.
即日回答お願いします.
某大学生 さんの書込 (2006/07/20(Thu) 08:16)
先ほどは間違えて投稿すみませんでした↓↓以下の問題(複素解析なんですが・・・)を,今日中にどなたか解いてもらえませんか?
1.f=u+iv(u,vはそれぞれfの実部と虚部)は複素数z=x+iyを変数とする正則函数とする.今fについて,その実部uが次で与えれられるとする.
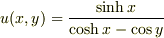
(1)Cauchy-Riemannの関係式を用いてy=0の時虚部が0になるようなfを求め,これをzの函数として表せ.
(2)Cを原点0を中心とする半径3πの正の向きを持つ円周とする時,(1)で求めたf(z)について 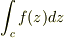 を求めよ.
を求めよ.
とりあえず一つ目です.
Re: 即日回答お願いします.
篠原 さんのレス (2006/07/20(Thu) 09:39)
はじめまして. 篠原です.
この問題に関して,何がわかりませんか??
> 今日中にどなたか解いてもらえませんか?
問題を丸投げして,完全解答が返ってくるとは思わないで下さい. 我々は便利屋さんではありません.
Re: 即日回答お願いします.
mNeji さんのレス (2006/07/20(Thu) 12:43)
はじめまして.
回答をお急ぎでしたら,ご自分で進めた分を示し,どこから出来なくなったかを明示してください.
そうしないと,短時間で満足のいく回答はできないでしょう.
この掲示板は,貴方や回答者だけにあるものでは無いです.多くの生徒・学生・その他の大勢の人々が情報の共有をしています.
Re: 即日回答お願いします.
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/20(Thu) 18:54)
とりあえずヒントだけ
- 適当な実関数
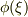 にたいして
にたいして 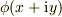 の実部を計算して与式になるようなものを探せばいいのでは?関数としては指数関数,三角関数,双曲関数くらいを探せばHITするのでは?
の実部を計算して与式になるようなものを探せばいいのでは?関数としては指数関数,三角関数,双曲関数くらいを探せばHITするのでは? - 分母が0になるところが複数あるので,それを探せばあとは手順通りのはず.
Re: 即日回答お願いします.
mNeji さんのレス (2006/07/20(Thu) 19:35)
少し計算してみました.
とにもかくにも指数関数に変換
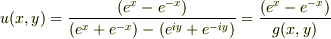
ここで
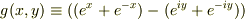
この関数は,yについて簡単だから,コーシー・リーマンの関係式の関係を念頭にyに付いて偏微分.ゴニョゴニョすると
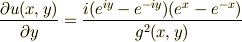
右辺を,xの偏微分で表現できるはずだとして,さらにゴニョゴニョすると
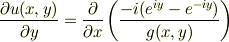
これとコーシー・リーマンの関係式 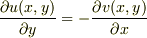 とを比較して,yの任意関数の不定性は残るが
とを比較して,yの任意関数の不定性は残るが
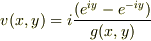
従って,求めるべき複素関数は,
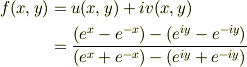
これから先, 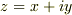 を使って,zの関数として,見通しの良い関数をどうすれば求まるのだろうか? ヘルプ・ミー!!!
を使って,zの関数として,見通しの良い関数をどうすれば求まるのだろうか? ヘルプ・ミー!!!
(以下のメモ:2006-07-21 (金) 12:19)
toorisugari no Hiroさんのアドバイスを受け,COさんのご推奨サイトを眺めた結果,とにもかくにも,見かけ上でも,独立な変数として複素数と共役複素数を導入する事にした,すると絶望的とも思える 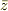 の消去ができたのである;
の消去ができたのである;
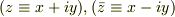
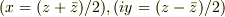
そこで
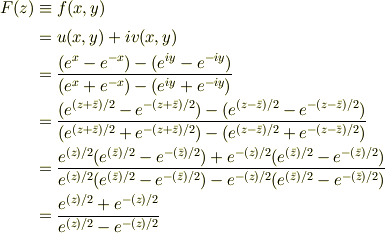
この関数は,少なくとも原点でポールを持つ.絶対値の大きな領域で1に漸近するので積分の収束性はどうだろうか.留数とか,また忘れている,とほほ.
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/20(Thu) 20:26)
なんか答えの符号違ってません?
この問題はもっとずるい(正統的な?)解き方もありますよ. (形式的には,解に3種類の形のヴァリエーションがあります.(指数関数表示は数にいれず:-)))
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/20(Thu) 20:50)
mNejiさんの場合,(修正のあと) 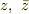 で書き直したらどうでしょう.
で書き直したらどうでしょう.
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/20(Thu) 21:06)
mNejiさんの解が正しいかどうか(符号の問題)は,ペンディングさせてください.(計算が合わない^^;;;)
Re: 即日回答お願いします.
Chappy さんのレス (2006/07/20(Thu) 21:15)
僕もtoorisugari no Hiroさんのおっしゃるとおりに, 与えられた関数に似た関数を調べてみました. 調べるとは大げさですが.
mNejiさんの解法でもやってみようと思います.
Re: 即日回答お願いします.
mNeji さんのレス (2006/07/20(Thu) 21:18)
>解が正しいかどうか(符号の問題)は,ペンディングさせてください.(計算が合わない^^;;;)
済みません,大雑把な計算をして,検算はまだです.その上,自分の所の簡易LaTeXと,こちらのTeXでの変換でもミスの可能性だいです.
ま,超初心者の計算例と言うことで,先にお進み下さい.もう少し検算してみます.
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/20(Thu) 21:30)
>解が正しいかどうか(符号の問題)は,ペンディングさせてください.(計算が合わない^^;;;)
わははは,コーシーリーマンの関係式を別の式と勘違いしてました(なまじ, 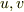 を使ってるから....).mNejiさんの結果で正しいです.すいません,すいません.
を使ってるから....).mNejiさんの結果で正しいです.すいません,すいません.
変換すると,割ときれいな形になりますよね. さらに半角を元の角にすると,もう一つ(訂正:2つですね)の解がえられます.
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/20(Thu) 21:56)
> 与えられた関数に似た関数を調べてみました.
この方法が一番簡単ですよね.コーシーリーマンの関係式から 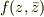 に制限がかけられますが,それと題意を組み合わせると
に制限がかけられますが,それと題意を組み合わせると  の関数形がすぐに得られますよね.計算力より論理力をみる(あるいはすごい腕力も可:-)問題ですね.
の関数形がすぐに得られますよね.計算力より論理力をみる(あるいはすごい腕力も可:-)問題ですね.
Re: 即日回答お願いします.
mNeji さんのレス (2006/07/20(Thu) 22:22)
検算する為に,逆の変数で微分しようかと思いましたが,目がくらんできたので降参しました.はやく数学ソフトが欲しいですね.
複素関数論は苦手だったので,やはり記憶の戻りも遅いみたいですね.宜しければ,
>> 与えられた関数に似た関数を調べてみました. > >この方法が一番簡単ですよね.
の方法をご伝授くださいませんか? 手元には「現代数学への入門 複素関数論入門,神保 道夫・著,岩波書店,2003-12, ISBN4-00-006874-1」があります.流体力学でも,そろそろ必要かと思うので....
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/20(Thu) 22:26)
>>この方法が一番簡単ですよね. >の方法をご伝授くださいませんか?
とりあえず,スレ主さんから有効な返答がない間は答えを出したくないので,明日の夕方以降でどうでしょう.(それに,テキストが必要なほど高級でもないですよ.COさんの示されたrefernce以上は必要ないです.)
Re: 即日回答お願いします.
mNeji さんのレス (2006/07/20(Thu) 22:57)
了解しました.COさんの示されたrefernce(英語は嫌いだ,なのですが)を見てみます.
Re: 即日回答お願いします.
mNeji さんのレス (2006/07/21(Fri) 12:29)
アドバイスに従って, 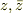 にして計算したら,zだけの関数になりました.→ No.10727に計算メモを書き込み.原点中心の線積分を求めるところをヘルプいただけると幸いです.段々,乱流の計算が見えかかってきたので,てへへ.
にして計算したら,zだけの関数になりました.→ No.10727に計算メモを書き込み.原点中心の線積分を求めるところをヘルプいただけると幸いです.段々,乱流の計算が見えかかってきたので,てへへ.
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/21(Fri) 13:01)
> アドバイスに従って, 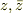 にして計算したら,zだけの関数になりました.
にして計算したら,zだけの関数になりました.
(^^)
この結果を双曲関数に書き換えると,きれいな形になります.
あるいは分子分母に 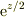 をかけると,計算が見通し良くなります.
をかけると,計算が見通し良くなります.
極は原点だけではないですよね. 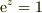 の解は?
の解は?
Re: 即日回答お願いします.
mNeji さんのレス (2006/07/21(Fri) 15:03)
>極は原点だけではないですよね.mbox{e}^{z}=1の解は?
ですね.つい, 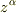 見たいなことしか浮かばなくて.半径3πからピンとこなかったのはお馬鹿さんでした.とすると,特異点は上下に計3ヶか.いよいよ残りは留数の定義を忘れてる.
見たいなことしか浮かばなくて.半径3πからピンとこなかったのはお馬鹿さんでした.とすると,特異点は上下に計3ヶか.いよいよ残りは留数の定義を忘れてる.
これまでのまとめ:
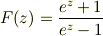
特異点は; 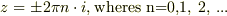
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/21(Fri) 16:57)
> ポールは; 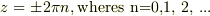 typoですよね?
typoですよね?
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/21(Fri) 19:42)
>>この方法が一番簡単ですよね. >の方法をご伝授くださいませんか?
実はもったいぶった割には大したことなくて恐縮なんですが....
正則関数だから 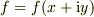 とおけます.
ここで
とおけます.
ここで 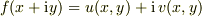 で,
で, 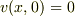 だから,
だから,
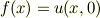
となります.  を
を  に置き換えて,
に置き換えて,
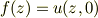
問題では 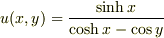 だから,
だから,
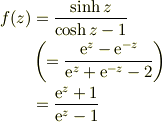
となります.
詐欺みたいですが,どんな 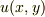 に対してもできるわけでなく
に対してもできるわけでなく
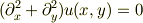
(訂正: および
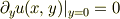
)が成り立つ  でないと
でないと  は存在しません.
は存在しません.
で,実際,  のcheckしたのかはムニャムニャムニャ(MapleさんはOKといった.)
のcheckしたのかはムニャムニャムニャ(MapleさんはOKといった.)
> 計算力より論理力をみる(あるいはすごい腕力も可:-)問題ですね.
訂正します.論理力→要領のよさ
Re: 即日回答お願いします.
mNeji さんのレス (2006/07/21(Fri) 21:28)
>正則関数だからf=f(x+mbox{i}y)とおけます. >ここでf(x+mbox{i}y)=u(x,y) +mbox{i},v(x,y)で,v(x,0)=0だから, >f(x)=u(x,0) >となります.xをzに置き換えて, >f(z)=u(z,0)
突然,宇宙人さんから話しかけられたようで,動転しています.(分かったのはmboxだけっだたり)
Q1 「v(x,0)=0だから」とは,どこから来るのでしょうか. Q2 「f(x)=u(x,0)」もどうして y=0と置けるのでしょうか. Q3 一連の手法はなにか定本がありますか?
こちらのレベルは漸く「コーシー・リーマンの関係式」を自分なりに消化できたところで,留数の計算がまだ出来ていないくらいですから,ゆっくりご教示くださいますか.
Re: 即日回答お願いします.
Chappy さんのレス (2006/07/21(Fri) 21:44)
いやぁ,すごい手法ですねー鮮やか! 僕の解法は普通です (^^;
mNejiさんはtoorisugari no Hiroさんの解説を待っていらっしゃるようなので, 僕は黙っとります...
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/21(Fri) 22:45)
すいません.だんだん,自信がなくなってきたので,あの解法はちょっとpendingにしてください.(矛盾が見つかったら教えてください.)
Re: 即日回答お願いします.
mNeji さんのレス (2006/07/21(Fri) 23:13)
>正則関数だからf=f(x+mbox{i}y)とおけます. >ここでf(x+mbox{i}y)=u(x,y) +mbox{i},v(x,y)で,v(x,0)=0だから, >f(x)=u(x,0) >となります.xをzに置き換えて, >f(z)=u(z,0)
なんども見ているうちに,例えば;
正則関数だからf=f(x+mbox{i}y)とおけます. ここでf(x+mbox{i}y)=u(x,y) +mbox{i},v(x,y)で,
そこで iy=0 と書いてみると, f(x+mbox{i}0)=u(x,0) +mbox{i},v(x,0)
すると,左辺では変数,z=xが実数だたら,zの関数f(z=x)も実数.
故に右辺のv(x,0)=0
従って,一般的に, f(x)=u(x,0)
が成立する.x → z と置き換えるのは自由だから,
f(z)=u(z,0)
f(z)に 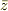 が含まれない限り,f(z)は正則関数である.
が含まれない限り,f(z)は正則関数である.
といった感じなのでしょうか?
====参考==== 正則関数 (数学解析)
Re: 即日回答お願いします.
Chappy さんのレス (2006/07/21(Fri) 23:17)
xからzに置き換えるのが少し怖くなってきました.
そのzも, 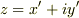 などと書けたら,
前に消されたyの立場がなくなってしまうような気がします.
ただの感想で申し訳ないですが...
などと書けたら,
前に消されたyの立場がなくなってしまうような気がします.
ただの感想で申し訳ないですが...
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/21(Fri) 23:45)
Q1,Q2は解決したと思うのでomitします.
> Q3 一連の手法はなにか定本がありますか?
すいません.知らないです.
>> 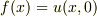 となります.
となります.
ここまでは問題ないと思うのですが,
>>  を
を  に置き換えて,
に置き換えて, 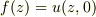
ここあたりは自分でも怪しい気分満載です.たぶん,解析接続とか一致の定理あたり関係あるかなと思っていますが,理解してるわけでないです.
これで作った 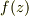 は本当に解析関数なんでしょうか?確かめてみましょう.
は本当に解析関数なんでしょうか?確かめてみましょう.
 の実部と虚部を
の実部と虚部を 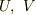 とおくと,定義により
とおくと,定義により
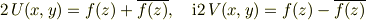
であり, 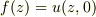 で
で  が実関数ですから,
が実関数ですから,
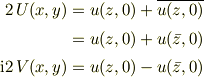
ですが,
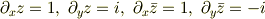
を考えると,
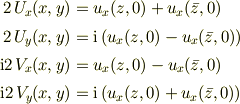
が得られます.これより
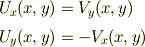
すなわち,コーシーリーマンの関係式が導かれので, 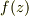 は解析関数です.
は解析関数です.
ただ,問題がまだあります.上の  と
と  は当然同一でなければいけません.つまり,整合性を得るためには
は当然同一でなければいけません.つまり,整合性を得るためには
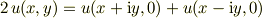
でなければいけません.これを満足する必要十分条件は
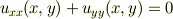
ではないかと思うのですが,必要性しかまだ導けていません.
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/22(Sat) 00:59)
> す,すいません.上の文で怪しいところみつけたので,また,pendingです.
未解決の問題がありますが,一応修正できたので,ご意見をお願いします.
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/22(Sat) 01:58)
だんだん重箱隅つつきになってきましたが,でた答えの実部が  と一致しなければ,ほかのやり方でも解けないぞと,ひらきなおっています.
と一致しなければ,ほかのやり方でも解けないぞと,ひらきなおっています.
> ただ,問題がまだあります.上のUとuは当然同一でなければいけません.つまり,整合性を得るためには > |30f707457c96c244afbf96f17c7fd55f| > でなければいけません.これを満足する必要十分条件は >
> ではないかと思うのですが,必要性しかまだ導けていません.
条件は
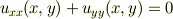
だけでなく
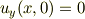
もです.これなら十分条件も満たしそうです,たぶん.(テーラー展開でいけそうなことは確認しました.きちんと証明してませんが.)
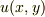 が調和関数であることはコーシーリーマンの関係式から自明なので,前者はよいとして,後者の解釈に苦しんでいます.たぶん虚部が
が調和関数であることはコーシーリーマンの関係式から自明なので,前者はよいとして,後者の解釈に苦しんでいます.たぶん虚部が 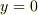 で消えることの補償だとおもうのですが,どなたかアドバイスもらえませんでしょうか?
で消えることの補償だとおもうのですが,どなたかアドバイスもらえませんでしょうか?
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/22(Sat) 02:10)
> どなたかアドバイスもらえませんでしょうか?
解決しました.
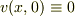 より
より 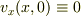 になりますが,コーシーリーマンの関係式
になりますが,コーシーリーマンの関係式 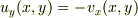 から
から 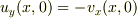 なので,
なので,
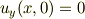
解釈は「虚部がy=0で消えることの補償」でOKですね.
調和関数であることと「虚部がy=0で消えることの補償」のふたつの条件を 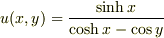 はともに満足することは確かめました.(ま,そうでなければ,どのような方法でも解は得られないですけど.)
はともに満足することは確かめました.(ま,そうでなければ,どのような方法でも解は得られないですけど.)
Re: 即日回答お願いします.
Chappy さんのレス (2006/07/22(Sat) 02:42)
深夜の所為なのか,変なことが気になります...
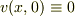 より,
より, 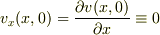 という結論に達したということは,
という結論に達したということは,
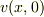 を
を  の一変数関数だと考えているわけですよね?
の一変数関数だと考えているわけですよね?
なぜ,僕がそう思ったのかというと,
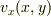 は
は 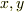 の2変数関数と思っていれば,
の2変数関数と思っていれば, 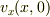 の意味は
の意味は
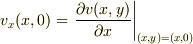 となりませんか?
となりませんか?
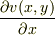 に
に 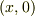 を代入したら,本当に0になりますか?
を代入したら,本当に0になりますか?
だから, 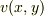 に
に 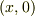 を代入したら,
を代入したら,
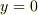 を代入したことになるため,変数
を代入したことになるため,変数  はありません.
すなわち,
はありません.
すなわち, 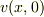 は恒等的に0な(
は恒等的に0な(  の)関数です.
したがって,
の)関数です.
したがって, 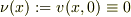 と置けますね.
そのとき,もちろん
と置けますね.
そのとき,もちろん 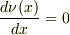 です.
です.
何かとてつもない勘違いを僕はしてるのでしょうか?
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/22(Sat) 03:02)
- レスポンスありがとうございます.深夜一人で重箱ほじくってる孤独に耐えられなくなったところでした.
> 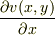 に
に 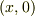 を代入したら,本当に0になりますか?
を代入したら,本当に0になりますか?
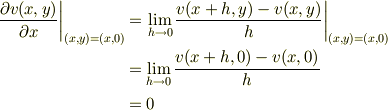
ではだめでしょうか.
Re: 即日回答お願いします.
Chappy さんのレス (2006/07/22(Sat) 03:18)
いやぁ,ほんと申し訳ないですが,,, 僕自身が疲れてると思うので,レスポンスをしないほうがいいと思うんですが, 気になって眠れそうにありません...
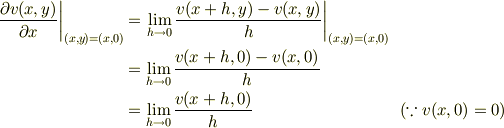
となりますが,極限 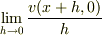 はどうなりますか?
はどうなりますか?
変な質問ですみません...
Re: 即日回答お願いします.
Chappy さんのレス (2006/07/22(Sat) 03:24)
度々すみません,自分でもわけが分からなくなっています. 明日の朝,改めて考え直してみることとします. くだらない質問に付き合っていただきありがとうございました.
Re: 即日回答お願いします.
Chappy さんのレス (2006/07/22(Sat) 03:41)
ああ!勘違いでした,ばかなことばかり言ってすみません... やっと眠れます...
Re: 即日回答お願いします.
mNeji さんのレス (2006/07/22(Sat) 11:35)
とても興味深い論議を拝見して,感銘しました.
と言うのも,少なくとも私には,複素関数論というのは,有用らしいが何かミステリアスな方法で,数学的センスのないものには高嶺の花という感じをしていました.
おそらく,このスレッドを立ち上げた学生さんも,私と同じように「なんだか宇宙人からの問題みたい」何ですけど?,という気持ちでヘルプをだされたと推測しています.
出来れば,今回の toorisugari no Hiroさんの手法を纏めて戴ければと思います.一番良いのは,Chappyさんのように toorisugari no Hiroさんも物理かぎプロジェクトに加入されて,記事として出されるのが最高と思います.
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/24(Mon) 17:38)
> 出来れば,今回の toorisugari no Hiroさんの手法を纏めて戴ければと思います.
では,長くなりますが,まとめてみます.問題の形で説明します.
(7/27: typo等 修正しました.)
問1. 実軸の一部を含む領域 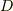 で定義された正則関数
で定義された正則関数 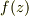 が,
が, 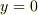 のとき虚部が
のとき虚部が  であるとする.
であるとする.
 の実部と虚部が
の実部と虚部が 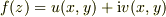 (
( 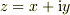 )と表せるとする.
)と表せるとする. 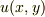 は以下の条件
は以下の条件
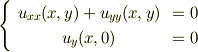
を満たすことを示せ.
- 領域
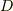 で
で 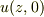 が定義され,かつ,正則関数なら,
が定義され,かつ,正則関数なら, 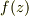 は
は
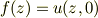
で一意に与えられることを示せ.
解答(1)
 が正則函数ならCauchy-Riemannの関係式により
が正則函数ならCauchy-Riemannの関係式により
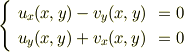
が成り立つ.よって,
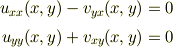
により
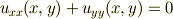
(  は調和関数)が示される.
また,題意より
は調和関数)が示される.
また,題意より 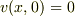 であるから,
であるから,
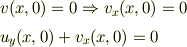
により
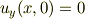
(虚部がy=0で消えることの補償)が示される.
解答(2)
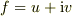 で
で 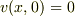 なので
なので
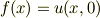
が成り立つ.題意により 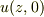 が正則関数だから,一致の定理(*)により
が正則関数だから,一致の定理(*)により
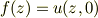
が成り立つ.
(*)一致の定理
「複素関数 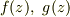 は領域
は領域 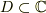 で正則であるとする.
で正則であるとする. 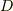 内の異なる2点を結ぶ滑らかな曲線
内の異なる2点を結ぶ滑らかな曲線 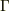 上で2つの関数が一致するならば,2つの関数は
上で2つの関数が一致するならば,2つの関数は 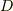 上で恒等的に等しい.」(証明は http://www.f-denshi.com/000TokiwaJPN/12cmplx/adxcmp02.html を参照のこと)
上で恒等的に等しい.」(証明は http://www.f-denshi.com/000TokiwaJPN/12cmplx/adxcmp02.html を参照のこと)
- をぐだぐだと証明していたのですが,これを示せば,
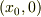 からのテーラー展開の級数が一致するという意味で
からのテーラー展開の級数が一致するという意味で
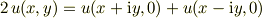
が証明できるからです.つまり, 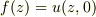 でつくった
でつくった  の実部は確かに
の実部は確かに 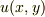 になります.しかし,これは「問題に意味があるか」(可解性)のcheckにすぎず,
になります.しかし,これは「問題に意味があるか」(可解性)のcheckにすぎず, 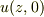 が正則関数であることが何かの手段でしめせれば,(2)だけ考えていればいいと思います.
が正則関数であることが何かの手段でしめせれば,(2)だけ考えていればいいと思います.
それを考慮した解法です.
問題 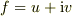 (
( 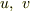 はそれぞれ
はそれぞれ  の実部と虚部)は複素数
の実部と虚部)は複素数 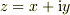 を変数とする正則函数とする.今
を変数とする正則函数とする.今  について,その実部
について,その実部  が次で与えれられるとする.
が次で与えれられるとする.
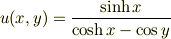
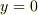 の時虚部が0になるような
の時虚部が0になるような  を求め,これを
を求め,これを  の函数として表せ.
の函数として表せ.
解答
正則関数だから 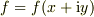 とおけます.
ここで
とおけます.
ここで 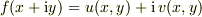 で,
で, 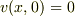 だから,
だから,
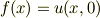
となります.
いま,  の引数の
の引数の  を
を 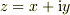 に置き換えた関数
に置き換えた関数 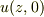 を考えます.
を考えます.
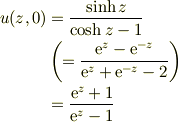
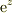 は正則関数だから
は正則関数だから 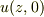 も
も 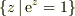 をのぞいた領域で正則関数です.
をのぞいた領域で正則関数です.
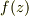 は正則関数で,
は正則関数で,  がなりたつのだから,一致の定理により
がなりたつのだから,一致の定理により
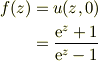
証明終わり.
(蛇足)
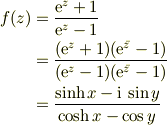
となり,確かに 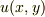 が実部になっている.
が実部になっている.
(p.s. mboxよりmathrmがよいです.>mNeji様)
Re: 即日回答お願いします.
mNeji さんのレス (2006/07/24(Mon) 18:28)
toorisugari no Hiroさん:
とてもユニークな方法をご丁寧に解説有難うございます.複素解析で悩む学生さんに心強いツールだとおもいます.そのうえ面白いサイトのご紹介まであって....是非とも一つの記事にしていただきたいと思います.
#「正則関数は,y=0で常に実数値となる」という定理を「toorisugari no Hiroの定理」と呼べると実に愉快ですね.→ それとなく数学の強い人々へ.
私も,この前後の論議を戴いて,とても参考になっています.そのお陰で,長年疑問に思っていた「正則関数」が理解できるような気になってきました.数学的に厳密な証明は出来そうにありませんが,写像の絵を使って説明するのが良さそうだと思います.
今日・明日と部屋の模様替えの為にじっくり読ませていただけませんが,ご連絡まで.
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/24(Mon) 18:39)
> #「正則関数は,y=0で常に実数値となる」という定理を「toorisugari no Hiroの定理」と呼べると実に愉快ですね
残念ながらそれは定理にはなりませんね. 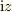 が反例ですから.
が反例ですから.
「実軸上で常に実数値となる正則関数 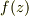 は
は
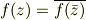
が成り立つ.(Schwarzの鏡像定理)」てのはありますけど.
> 是非とも一つの記事にしていただきたいと思います
おもしろい記事にするのは,それはそれで,また大変です.mNejiさんにお願いできないかな?(勉強になりますよ,と誘惑してみる.)
Re: 即日回答お願いします.
mNeji さんのレス (2006/07/24(Mon) 19:06)
>残念ながらそれは定理にはなりませんね.mathrm{i}zが反例ですから.
これは正則関数ではないような気がします.と言うのも「純虚数」を作るにはだけでは無理がある.C-Rでも説明できるでしょうが.
で,段々と「正則関数f(z)」とは何kさ?という疑問がどんどんと成長してしまう訳で.
>おもしろい記事にするのは,それはそれで,また大変です.mNejiさんにお願いできないかな?(勉強になりますよ,と誘惑してみる.)
今のところ,流体力学に速く手を出したいわけで... 確かに2次元問題というのは,素人のモデル計算にとっては必須のツールであることは良く理解できて来たのですが.自分は「渦のモデル計算」を目に取れるようにしたいので...
とりあえず,『正則関数のu(x,y)が与えられたとき,v(x,v)をいかにスマートに得る方法』はTipsの一つにはしたいですね.どうしたらいいか,→ やはり若き数学系のひとのお力をヘルプしたいなぁ.
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/24(Mon) 19:38)
> これは正則関数ではないような気がします.
? それだと わき出し
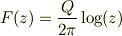
渦糸
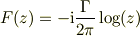
のどちらかが(原点以外でも)正則関数じゃないことになってしまいますが?
ちなみに先の問題は一列に並んだわき出し/渦糸の問題ですよね. (十分遠方では「速度(の複素共役)」が一様になる)
Re: 即日回答お願いします.
mNeji さんのレス (2006/07/24(Mon) 20:53)
>>残念ながらそれは定理にはなりませんね. 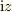 が反例ですから.
>これは正則関数ではないような気がします.
が反例ですから.
>これは正則関数ではないような気がします.
前言撤回します.
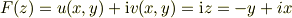
故に


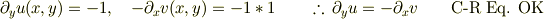
ですね.まだ理解できていない,正則関数.情けない.
Re: 即日回答お願いします.
mNeji さんのレス (2006/07/24(Mon) 21:18)
>ちなみに先の問題は一列に並んだわき出し/渦糸の問題ですよね.
これは理解している筈です.まだ留数*3を出してませんが.
>(十分遠方では「速度(の複素共役)」が一様になる)
こちらは?
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/24(Mon) 21:40)
>> (十分遠方では「速度(の複素共役)」が一様になる) > こちらは?
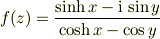
より
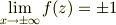
これは 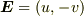 とおけば(
とおけば( 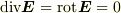 が成り立ちます),
が成り立ちます), 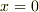 にある金属板に電荷を分布させたときの静電場に十分遠方で等しいことを意味します.
にある金属板に電荷を分布させたときの静電場に十分遠方で等しいことを意味します.
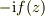 とおけば渦面(?)がつくる速度場
とおけば渦面(?)がつくる速度場 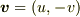 に対応します.(
に対応します.( 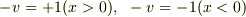 )
)
Re: 即日回答お願いします.
mNeji さんのレス (2006/07/24(Mon) 22:19)
まだ理解未消化でありますが,とても興味深いことが,複素関数論の背後にあることは理解できます.
ついては,私からご提案させて戴きたいのですが
- No.10886のtoorisugari no Hiroさんのご解説
これを出来ましたらコピー戴いて,新しいスレッドを建てていただけませんでしょうか.これに付いての質問は,以後,そのスレッドでお尋ねできれば幸いです.
- 複素関数論の勉強についての質問
というようなスレッドを私が立てます.私は,冗談抜きで,複素関数論には手を出さないようにしていました.せいぜいコーシー・リーマンの関係式からポアッソンの式を誘導するところまでです.
今回のこのスレッドを拝見するまで,自分で偏微分するなど考えても見ませんでした.その意味では,この質問を出された某大学生さんには,いい経験をさせて戴けたことを感謝します.
ですから,虚数一発で,「湧き出し」や「渦糸」が出てきたり,電場もどきが出てきたり,本当にびっくりデス.これまでは「目を瞑っていた」のだと,...お恥ずかしい.
宜しく,ご指導お願いします.
Re: 即日回答お願いします.
toorisugari no Hiro さんのレス (2006/07/24(Mon) 22:31)
> 1) No.10886のtoorisugari no Hiroさんのご解説 > これを出来ましたらコピー戴いて,新しいスレッドを建てていただけませんでしょうか.これに付いての質問は,以後,そのスレッドでお尋ねできれば幸いです.
私もこの議論でいろいろ勉強できたので新しいスレッドで議論をすすめることはうれしいのですが,この掲示板の性格上,質問もなしに新しいスレッドはたてつらいので,
お手数ですが,適当な箇所をコピペされて,質問でも感想でも書いていただくと,スレッドをつづけられるのですが.
Re: 即日回答お願いします.
toolkit さんのレス (2006/07/27(Thu) 01:06)
toorisugari no Hiroさん:
>私もこの議論でいろいろ勉強できたので新しいスレッドで議論をすすめることはうれしいのですが,この掲示板の性格上,質問もなしに新しいスレッドはたてつらいので,
>お手数ですが,適当な箇所をコピペされて,質問でも感想でも書いていただくと,スレッドをつづけられるのですが.
申し訳ありません,この部分を見過ごしていました,お詫び申しあげます.m(_._)mmmm
ちょっとドタバタが続いているのと,明晩,Chappyさんが試験から解放されて,コーシー・リーマンの関係式に関わる論議をしてくださるようなので,これを踏まえて,toorisugari no Hiroさんの解説を引用して別途質問を立てるようにいたします.
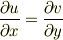
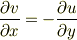
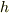 は実数じゃないのですか?実数なら
は実数じゃないのですか?実数なら 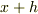 も実数ですよね.
も実数ですよね.