解析力学の定義的なものについて
解析力学の定義的なものについて
サンダーSP さんの書込 (2006/07/19(Wed) 01:40)
こんばんは. 今回は,前に比べもうちょっとまともな質問をさせていただきます.
興味から,2,3年早い?解析力学の勉強を始めたのですが,不可解な箇所が幾つかあり,使っている参考書(?)ではごまかし?があり,検索もしましたが,きちんとした説明を見つけられませんでした. なので救いの手をお願いします.
*一般化運動量の定義 まず最初に,p=bq'(bはqが長さの次元なら質量,無次元なら慣性モーメントに相当するもの)と定義がされており,後からp=∂T/∂q'と再び定義し,これは先ほどの定義と実際に矛盾しないので,OKという風に説明がありました. ネットで検索すると,全て後者の定義になっており,前者に関するものは見つからなかったのですが,これは(円柱等の一般の座標系で)本当に成り立つのでしょうか? 考えてみましたが,どうやって確かめたらいいのかさえ分かりません. 多分,一般化座標が式の上だけで定義されているためか,いまひとつ分かりきっていないというのもあるかもしれませんが・・・
*Uがq'の値による時のラグランジュ ラグランジュの方程式を導く過程で,∂U/∂q'=0を使い,後でUがq’の関数でもある時の説明をすると書かれており,その考察がローレンツ力に関する問題を取り上げ,確かに書かれていましたが,いい加減?になっています. その箇所を暴力的に言えば,ラグランジュ方程式で解いた場合と,普通に求めた場合の結果が一致するから,気にする必要が無い,というように書いてありました. なぜ成り立つのでしょうか?
ちなみにこの本というのは,アマゾンの項目を拝借すると, http://www.amazon.co.jp/gp/product/4061545094/250-2972973-8865847?v=glance&n=465392 です. 1つ目の質問の出所:P83,85,2つ目の質問の出所:P119 あと,もし解析力学で良書がある(と推奨できる),って言う方いらっしゃいましたら,是非教えてください.(出来れば高校生でも理解できるというものを)
Re: 解析力学の定義的なものについて
mNeji さんのレス (2006/07/19(Wed) 02:08)
はじめまして.
>もし解析力学で良書がある(と推奨できる),って言う方いらっしゃいましたら,是非教えてください.(出来れば高校生でも理解できるというものを)
もしも貴方が,微積分が堪能で,ベクトル解析もマスタしたというならば,良い解説 書が,さまざまな特徴をもって存在していると思います.
でも,数学的な基礎が無いままに,中途半端な本を読むのはやめるべきと思います.
その代り,高校の物理の範疇の問題でも;
・慣性系で運動方程式を立て, ・解き易い系(多くの場合,非慣性系,ない被加速系)で, 慣性系での運動方程式を書き換え ・見かけの力がどのように出現してくるかを的確に判断し ・初期条件に適合した解を得る,
上記の過程をじっくりと習得するべきと思います.間違っても,大量の問題を解くのに勢力を注ぎ込むのはやめましょう.むしろ,回答を流れのあるストーリとして作る練習をしたほうが良いと思います. ・物理の物語を,数式を通して書く. ・慣れるに従って,作文形式 → 俳句形式 と簡潔に! ・そして最後は,要点の式だけ 感じだとおもいます.こうしておくと,検算が楽で,修正点も判り易い!
その代り,数学は一歩進めて自分で予習してしまいましょう. 1) 複素数 → オイラーの公式 2) 2次方程式の虚根を含めた解の意味 3) 1次全微分方程式(同次)を解く,非同時(強制力)のある場合も含める. 4) ベクトル解析の基礎:偏微分 5) 2次全微分方程式(同次)を解く,非同時(強制力)のある場合も含める. 等々.(掲示版に来てからの,所感なので議論がこなれていませんが...)
そして,amazonの例で挙げられた本は,見ないほうが良いと思います.私も,流体力学を勉強初めています.そのシリーズの「流体力学」を拝見しましたが,「で何?」の世界と思いました.
あと,時間に余裕があるなら,数学と同程度の重みで,「英語」の基本文法+語彙は少しずつ拡大に努めるべきと思います.← 自己反省の結果!
Re: 解析力学の定義的なものについて
サンダーSP さんのレス (2006/07/20(Thu) 00:28)
アドバイスをありがとうございます.
>でも,数学的な基礎が無いままに,中途半端な本を読むのはやめるべきと思います.
確かにその通りだと思います.高校の物理を半分独学で進め,だいたい理解したので,ちょっと大学の物理でもかじってみようと思い,ほぼ一年前くらいに初めて大学物理の参考書を手にとってみたいのですが,数式の羅列で,理解しようにも理解不能でした.
>もしも貴方が,微積分が堪能で,ベクトル解析もマスタしたというならば,良い解説書が,さまざまな特徴をもって存在していると思います.
じゃあまだまだ先の事となりそうです(結局は大学に入ってからになるのかな).特に積分なんかまだまだ不完全で,電磁気と絡むベクトル解析もテンソルくらいになるとギブアップなので. 後その下に書かれている項目も,微分方程式なんか1次の変数分離型しか知らないので,やはりもっと数学の方を勉強しなければいけなそうです.
>上記の過程をじっくりと習得するべきと思います.間違っても,大量の問題を解くのに勢力を注ぎ込むのはやめましょう.むしろ,回答を流れのあるストーリとして作る練習をしたほうが良いと思います.
これがイマイチよく自分の中でイメージしにくい気がします. 自分は問題を解くとき,可能な限りの関係式(方程式)を先に立てて,そのまま連立して解く形をとっているのですが・・・
Re: 解析力学の定義的なものについて
mNeji さんのレス (2006/07/20(Thu) 01:21)
>確かにその通りだと思います.高校の物理を半分独学で進め,だいたい理解したので,ちょっと大学の物理でもかじってみようと思い,ほぼ一年前くらいに初めて大学物理の参考書を手にとってみたいのですが,数式の羅列で,理解しようにも理解不能でした.
なかなか頼もしい限りですね.でもその余裕は,高校生という現時点で必要な能力開発に注入しましょう:数学や英語.むしろ物理は,大学でよい講義を聴きながら勉強できるのですから.一方,大学で,教養の物理を教える側では,数学の講義とリンクして教えていないので,どうしても歪が学生に押し付けられると思います.
私も,高校の物理はさておいて,自分で勉強していました.でも,数学は普通に受けていました.当時は,複素素数がホンの少ししかない時代だったので,オイラーの公式;
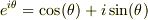
は,全くの別世界のものと思い込んでいました.でも,こんなに便利なツールを使いこなさないのは,むしろ不自然とおもいます.テストでは三角関数しか使っていけないとしても,答えに到達するまでを 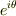 でだし,必要なところだけ三角関数に戻せば良いのではと思っています(笑).
でだし,必要なところだけ三角関数に戻せば良いのではと思っています(笑).
>じゃあまだまだ先の事となりそうです(結局は大学に入ってからになるのかな).特に積分なんかまだまだ不完全で,電磁気と絡むベクトル解析もテンソルくらいになるとギブアップなので.
電磁気は,力学に比べて基礎方程式が多い上に,「真空での挙動」「物質中での挙動」で話が込み入ります.ですから,素人である新1年生は,専門家である先生の大まかな筋書きを聞いたうえで,自分の勉強を定めて行くのが賢明だろうと思います.
私なんか,テンソル(テンサ)はきちっと勉強しなかったので,こちらのサイトで,Johさんの解説をみて再勉強しているぐらいですから....
>後その下に書かれている項目も,微分方程式なんか1次の変数分離型しか知らないので,やはりもっと数学の方を勉強しなければいけなそうです.
ここまで来ていれば,ln(x),exp(-λt)を微分方程式の解と感じ取れる分けですよね.それなら2次方程式の解を理解できれば,さい次2階微分方程式を理解するのは楽勝だと思います.と言うのも,力学の運動方程式で,回転が入った運動を明確に理解する為に,如何にして2階微分方程式を早めに取り扱えるか,と考えた結果です.要は,私の勝手な主張です(笑).
>これがイマイチよく自分の中でイメージしにくい気がします. >自分は問題を解くとき,可能な限りの関係式(方程式)を先に立てて,そのまま連立して解く形をとっているのですが・・・
これは,人それぞれと思います.プログラムもそうですが,式を出していく時,簡単なコメントつけると,見直すときにとても効率がいいです.
恐らく,テストでも,検算プロセスの効率までいれると,要所にコメントをつけた方がいい効率(高い点数)が得られると推測されます.
そこら辺は,なにか具体的な疑問点が浮かんだときに,書き込んでいただければ具体的に論議できるとおもいます.
マイペースを守りながら,青春を楽しんで,知恵を磨いてください.
Re: 解析力学の定義的なものについて
Joh さんのレス (2006/07/20(Thu) 01:52)
サンダーSPさん,
高校生で解析力学を勉強なされているということで,驚きました.高校生用に書かれた解析力学の本というのは知りません.(恐らく無いでしょう.)しかし,私が良書と思うものなら紹介できます.
*力学(ランダウ・リフシッツ)東京図書 *古典力学(ゴールドシュタイン)吉岡書店
難しい部分もあると思いますが,がんがんチャレンジしたらいいと思います!年齢とか,数学の素養とか関係ないですよ.足りない部分があれば,後から勉強したらいいんですしね.まぁ,無理しないで下さい.今後,何を勉強すべきか,どんな世界がこの先広がっているのかが分かれば十分な収穫です.
最初の質問のほうは・・・,難しそうなので復習してから出来れば一緒に考えてみたいと思います.ムム
Re: 解析力学の定義的なものについて
toorisugari no Hiro さんのレス (2006/07/20(Thu) 02:35)
高校生向きではないですが,ゴールドスタインがでたならこの本も紹介しないと(^^).
- http://www.amazon.co.jp/gp/product/4061532413/ 量子力学を学ぶための解析力学入門 高橋 康
高橋さんの本は全部気にいっています.
Re: 解析力学の定義的なものについて
サンダーSP さんのレス (2006/07/21(Fri) 01:14)
*No.10713に関する返答 >でもその余裕は,高校生という現時点で必要な能力開発に注入しましょう:数学や英語.
数学も結構好きなので,学校の勉強はしていますが,確かに英語とかは徐々に成績が落ちてきているように感じます.
ちなみに最近では物理を完全に大学レベルと高校レベルに分けてしまい,前者を趣味的なもの,後者を勉強と見なしています.(でも勉強だと思うと,なぜかやる気が無くなる・・・)
>当時は,複素素数がホンの少ししかない時代だったので,オイラーの公式; は,全くの別世界のものと思い込んでいました.でも,こんなに便利なツールを使いこなさないのは,むしろ不自然とおもいます.
確かにオイラーの公式なんかは最初知った時,驚きました.全く別の所から湧いて出たような自然対数と三角関数,複素数が一つの公式として出てきていて. ちなみに最近その証明法を知り,その時も感動しました.(テイラー展開の証明理解できてないのに・・・)
>マイペースを守りながら,青春を楽しんで,知恵を磨いてください. mNeji様,ありがとうございます.
*No.10714に対する返答 本のご紹介ありがとうございます. しかし利用している図書館の蔵書検索をしてみましたが,どうやらどちらも無さそうです.機会があれば取り寄せで見てみようと思います.
>年齢とか,数学の素養とか関係ないですよ.足りない部分があれば,後から勉強したらいいんですしね.
そうですよね.ただあまりにも足りなさ過ぎて,つまずく事が多いですが.
最初のした質問については,また半日なり一日なりつぎ込んでゆっくり理解&整理しつつ,もっといろいろな方向へ進もうと思います.そこでまた別の質問をさせていただくかもしれません.
*No.10715に対する返答 すごく読んでみたい本です.僕が解析力学を勉強した主意は,量子力学に繋がりますので.でも,やはりどっちの図書館には無さそう.
Re: 解析力学の定義的なものについて
Chappy さんのレス (2006/07/21(Fri) 01:56)
サンダーSPさん,はじめまして,Chappyというものです.
それほど関係のない返答ですが,
テイラー展開の証明は理解できなくてもよいと思いますよ.
実際に定理を使うことができて,
テイラー展開のイメージがあればよろしいと思います.
最初は大まかに近似
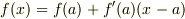
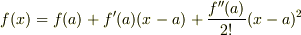 だんだん近似を細かく・・・・
だんだん近似を細かく・・・・
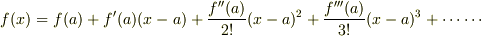 こんな感じでよいのではないでしょうか.
こんな感じでよいのではないでしょうか.
- http://www.geocities.jp/nekobeya1204/math/taylor/taylor_graph_overpic.gif
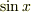
- http://www.geocities.jp/nekobeya1204/math/taylor/taylor_graph2_overpic.gif
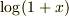
を参考にしてみてください. 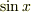 はうまく行きますが,
はうまく行きますが, 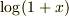 は原点から遠ざかるとうまく行きませんね.近似曲線のグラフが必死で(?),点
は原点から遠ざかるとうまく行きませんね.近似曲線のグラフが必死で(?),点 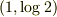 の地点に近づこうとしてる様子が分かると思います.その理由を考えてみるのも数学です.まぁ,数学の問題を振るのは場違いですね (^^; 聞き流してください.
の地点に近づこうとしてる様子が分かると思います.その理由を考えてみるのも数学です.まぁ,数学の問題を振るのは場違いですね (^^; 聞き流してください.
Re: 解析力学の定義的なものについて
CO さんのレス (2006/07/21(Fri) 09:46)
こんにちは.
> テイラー展開の証明は理解できなくてもよいと思いますよ.
私も高校の時点でテーラー展開を理解している必要はないと 思いますが,知っていて損はないとも思います.
私が高校生のときに学んだテーラー展開の証明法は次のような 部分積分を使うものでした.高校数学の知識で読めます.
数学的には誤魔化しが入っているのかもしれませんが..
Re: 解析力学の定義的なものについて
toorisugari no Hiro さんのレス (2006/07/21(Fri) 12:33)
> テーラー展開の証明法は次のような部分積分を使うものでした.
私が教わったのはもっといい加減な方法です.
基本は 「恒等式がなりたつなら任意の場所の等式もなりたつ」
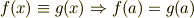
と「恒等式の微分は恒等式」
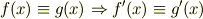
です.
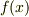 を多項式で近似したいと考えます.
を多項式で近似したいと考えます.
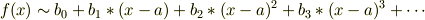
ただし, 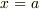 の近傍では近似の精度は非常によいとして,
(「物理屋」モード!)恒等式と考えます.
の近傍では近似の精度は非常によいとして,
(「物理屋」モード!)恒等式と考えます.
あとは上の手順を繰り返すだけ.
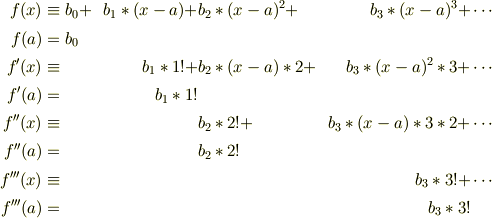
「無限に続く」です.
Re: 解析力学の定義的なものについて
yama さんのレス (2006/07/21(Fri) 14:45)
最初の質問の一般化運動量の定義について答えておきます.
一般化運動量の初めの定義は正式なものではなく,導入段階で便宜上定めたものだと思います.これが後の定義と矛盾しないことは次元を考えれば分かります.
まず,Tは運動エネルギーなので ![[ML^2T^{-2}]](http://hooktail.maxwell.jp/bbslog/09908b783a8fb210b613e79ab6d4d88b.png) の次元を持ちます.q が長さの次元を持つ場合は,q' は
の次元を持ちます.q が長さの次元を持つ場合は,q' は ![[LT^{-1}]](http://hooktail.maxwell.jp/bbslog/f376b1d577ac0b2bcd4a0ee70ea3df02.png) の次元を持ちます.
従って一般化運動量 p=∂T/∂q' の次元は,
の次元を持ちます.
従って一般化運動量 p=∂T/∂q' の次元は, ![[ML^2T^{-2}]/[LT^{-1}]=[MLT^{-1}]](http://hooktail.maxwell.jp/bbslog/50c6e81b08fe107656758b014b4b30ee.png) になります.これは質量とq' の積の次元に等しいことが分かります.
同様に,q が無次元のときは, p=∂T/∂q' の次元は,
になります.これは質量とq' の積の次元に等しいことが分かります.
同様に,q が無次元のときは, p=∂T/∂q' の次元は, ![[ML^2T^{-2}]/[T^{-1}]=[ML^2T^{-1}]](http://hooktail.maxwell.jp/bbslog/a0355c592551b1509b838e6a1a776f2f.png) になります.これは慣性モーメントとq' の積の次元に等しくなっています.
具体例として円柱座標の場合を考えてみます.
になります.これは慣性モーメントとq' の積の次元に等しくなっています.
具体例として円柱座標の場合を考えてみます.
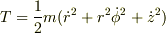 だから,一般化運動量は次のようになります.
だから,一般化運動量は次のようになります.
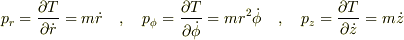
 は質量であり,
は質量であり, 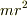 は慣性モーメントに相当すると考えることができます.
は慣性モーメントに相当すると考えることができます.
Re: 解析力学の定義的なものについて
mNeji さんのレス (2006/07/22(Sat) 18:52)
少々遅すぎたかもしれませんが,アドバンストな高校生さんにややお勧めと思える本:
現代数学への入門・力学と微分方程式 高橋 陽一郎・著, 岩波書店,2004-02, ISBN:4-00-006875-X
これは「シリーズ 現代数学への入門」全16冊の一つらしいです.と言うのも,私も,偶然,近くの図書館で見ているうちに,良い本らしいと思い始めているだけですし,全部が発行されているかも知りません.
この本の「まえがき」からすこし引用させていただきますと;
シリーズの『微分と積分1,2』『複素関数入門』に引き続いて,17世紀のニュートンやライプニッツに始まる「無限小解析(infinitesimal calcus)」とその延長線上にある解析の世界を紹介する.やさしく基本的なものを,基本的であることを明確にしながら,理解しやすく記述することの難しさを,2冊目の執筆を始めてから,より強く感じるようになった. 常微分方程式とその周辺は,すでに300年以上の歴史をもち,...
恐らく,この本の想定読者は,大学2年生で,教養の力学や数学を終えた人が,複雑な解析力学周辺に取り付くまえに,頭を整理するような感じで説明している.
ある意味では,大学生でドンドン先に行きたがりの方々には,「まどろこしい」かもしれない.逆に,おませな高校生が,いま習っている常微分方程式が物理の基礎にドデンと存在することを垣間見るいい本tもおもえる.
ですから,読者にたいして,サービスとして出てくる「惑星での面積速度一定の法則」,p3からp4 などは,高校生にとっては無意味な解説になってしまうかもしれない.そんな時は,少し飛ばしてp5をみると,

などから読み出せばいいようです.
===== 常微分方程式つながり:インターネットで下記のサイトがあります.2階の場合ですが,良く書けていたと思います.
8 線形常微分方程式 ・ http://www.geocities.jp/ruy406/math/math8.pdf#search=
Re: 解析力学の定義的なものについて
yama さんのレス (2006/07/22(Sat) 21:34)
mNejiさん紹介の上記のサイトは,分かりやすくまとまっていると思います. もう少し詳しい説明や,いろいろな例題については,このサイトの管理者による下記の図書が参考になると思います.
この本の初版は,著者が大学3年のときに出版されています. ベクトル解析や複素関数など大学の理系で学ぶ数学の主要な内容が説明されていて,定理や公式の証明もきちんと書かれています. 説明も分かりやすくていい本だと思います.
Re: 解析力学の定義的なものについて
サンダーSP さんのレス (2006/07/23(Sun) 01:23)
>>No.10752 はじめまして. マクローリン展開によるf(x)=sin xのグラフは,Excelで前に描いた事がありますが,x=2*3.14159…(ちなみに昨日は円周率の近似値の日とされているそうです(7/22))あたりで10次までの計算だと,誤差が40くらいになってしまい,本当に使えるのかなと疑問に思った事もあります.
>>No.10761&No.10765 ありがとうございます.部分積分からの証明,なかなか分かりやすいです.(ただ6行目の上端と下端が逆のように思えて仕方ないのですが 後者の無限に足し合わせる方法も理解できるにはできますが,むしろ最初の恒等式とかについての式の方が難しいように思えました.
>>No.10767 次元は一応確認して,次元が成り立つ事はよく分かりました.質問後ずっと考えていたのですが,直交座標や,それに変換が簡単に可能な極座標では,T=(1/2)*m*(速度)^2となり,p=bq'と定義できるのがすぐに分かりますが,その他の任意の座標系で成り立つと言われるとどうもイメージできません.
>>No.10836&No.10842 タイトルだけ見てると,とてもハードルの高そうな本に見えますが,そうでもなさそうですね.(Amazonのレビューを見てみると) とりあえず微分方程式については,まず前々から読んでいる物理数学に関する本できちんと勉強しようと思います.(結構分かりやすいので)