波とエネルギは振幅
波とエネルギは振幅
とも さんの書込 (2006/07/18(Tue) 21:21)
なぜ波のエネルギは振幅(または圧力,速度)の二乗と比例するのですか? すいませんもう一度教えてもらえるとうれしいです...
Re: 波とエネルギは振幅
mNeji さんのレス (2006/07/18(Tue) 22:20)
前回;
いま直ぐには,直接的な回答が出来ませんが.代わりに電気の場合で考えて見ます.電気と音響は似ているところがありますね.初めは簡単の為に,直流の電気で考えます.
電圧V = 抵抗(インピーダンス)Z*電流J 消費電力P = V*J = Z*J*J = Z*J^2 =V^2/Z
音波は交流に似ていますが,計算が面倒になります.係数の1/2は交流場合,その時間平均を決める定義により出てきます.
と書きましたが,この説明の何処が判らないか教えてください.
また事業では,音響の波動方程式とか教えていただいた内容を書いていただけませんか? 詳しく説明するには,波を記述する数式がないと説明も理解も難しいですよね.
Re: 波とエネルギは振幅
とも さんのレス (2006/07/18(Tue) 22:45)
説明していただいたことは分かったのですが,そこからどうやって振動につなげるかが分かりません.
学校では授業をせずに実験に入ったので式は知りません. しらべて,
の波動方程式の説明を見ましたが,僕には難しすぎました.
Re: 波とエネルギは振幅
とも さんのレス (2006/07/18(Tue) 23:16)
他のサイトにも同じ質問をしていたのですが,分かりました!
>一般に空気やスプリングは圧力に比例して縮んだり伸びたりします. 振動のエネルギーは最大に縮んだ(または伸びた)時に蓄えられるエネルギーです. バネや空気の場合,力は自然の状態(0)から最大に振れた時(振幅に比例)の間で比例して変わる. 平均の力は最大に振れた時の1/2 となる. エネルギーは力*移動した距離(振幅の半分)ですから 振幅の2乗に比例する.
だそうです. 本当に説明ありがとうございました! 掲示板にかきこむことを初めてしたので無礼なことをしてしまったかもしれません.(汗 また機会があれば質問しに来ます. 遅くまでありがとうございました!!
Re: 波とエネルギは振幅
mNeji さんのレス (2006/07/18(Tue) 23:22)
波といっても多種・多様なので,波のできる現象によって波の意味が其々によって異なります.
そこで,音響を考えて見ます.更に,問題を簡単にするために耳の中の鼓膜に到達した波を考えます.
最近,粗密波というスレッドがありましたが,音響波はその粗密波,言い換えれば進行方向に空気の圧力の変動が起こるものです.
さて耳のところでの空気の圧力は時間の関数で表せます. さらに問題を簡単にするために,音源が「音叉」のように一定の周波数だとします.普通,音叉は「ラ:A」でf=440Hzぐらいですね.
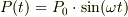
ここで, 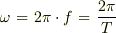
この波が鼓膜を動かします.鼓膜の中央部はこの波によって,そのまんま動くとしてもよいでしょう.そうすると膜の微小部分の質量をmの変位D(t)は
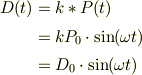
従って,その運動エネルギK(t)は
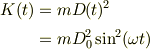
のような形になります.このような波の運動エネルギが音の大きさIとして認識されるばあい,その時間平均が意味を持ちます.
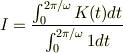
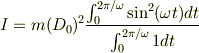
ここで
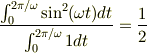
故に
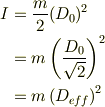
ここで振幅の実効値 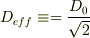
といった感触.