中心力

中心力

ta さんの書込 (2006/07/18(Tue) 19:43)

こんにちは．大学で物理を学んでいる者です．過去問なのですが，みんなで頭を悩ませているのですがどうも解法がわかりません．どなたかご指導いただけないでしょうか．

問題）中心力とは，方向が常に力の中心方向を向き，大きさが力の中心までの距離ｒだけの関数となる力である，すなわち，位置ベクトルｒの地点での中心力Ｆ1はＦ1＝ｆ(r)ｒと表せる．（ここで，ｆ(r)はｒの関数．また，ｒの大きさがrとなる．） (1)中心力Ｆ1は保存力となることを示せ． (2)質量ｍの質点に，中心力Ｆ1だけが作用しているとき，質点は力の中心を含む１つの平面内を運動することを示し，その平面での力の中心を原点とする平面極座標(r,θ)を用いて運動方程式を書き表せ． (3)質点が運動する平面で，力の中心を原点とした直交座標(x，y)を用いると，質点がx^2/a^2 + y^2/b^2 = 1という楕円（a,bは定数）の上を運動している場合には，f(r)はrに依存せず一定となることを示せ．

ベクトルｒとrが見分けにくくてすいません．(1)はおそらく偏微分をすればよいと思うのですが，(2)以降がわかりません．どなたかお願いします…．

Re: 中心力

mNeji さんのレス (2006/07/18(Tue) 20:07)

はじめまして．

以前，類似の質問があったので，調べたのですが，

  1. に付いては，この掲示版に回答したので，「中心力」「保存力」などで検索してみてください．

(2)についても教科書を見ていただくしかないと思いますが...

例えば，下記のサイトをご覧になり，

・物理学セミナー 2004May20 林田清・常深博（阪大）

そのどこら辺が納得できないかお示しくだされば，一緒に考えたいと思います．

(3)について 直交座標の原点に中心力の原点があるならば，(2)の結論と矛盾しませんか？

Re: 中心力

ta さんのレス (2006/07/18(Tue) 23:05)

遅れてすいません…．一通りは読んだのですが，(2)は具体的にはどの式を使えばよいのでしょうか…？

Re: 中心力

ta さんのレス (2006/07/19(Wed) 01:07)

やっぱりそこですよね．なんとなく分かったような気がします…．では，(3)については問題が間違っているのでしょうか…？

Re: 中心力

yama さんのレス (2006/07/19(Wed) 01:09)

(2)の前半については，角運動量の保存を利用して示すことができます． 角運動量が一定ということは，角運動量ベクトルが常に一定の方向を向き，それに垂直な平面内に運動量ベクトルがあるということだからです． 運動量 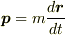\bm{p}=m\frac{d\bm{r}}{dt} を用いると運動方程式 は 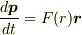\frac{d\bm{p}}{dt}=F(r)\bm{r} となりますが，これを利用すれば 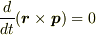\frac{d}{dt}(\bm{r}\times\bm{p})=0 を示すことができます．

(3)はそのような楕円運動になるような中心力は，中心からの距離に比例する引力になることを示すわけですが，この逆の問題，すなわち距離に比例する引力がはたらくときの運動がNo.10308で議論されているので，参考にしてください．

Re: 中心力

ta さんのレス (2006/07/19(Wed) 01:29)

返信ありがとうございます．(2)の後半の式が分かりそうで分からないのですが…．普通の極座標と同じでx=rcosθ,y=rsinθと考えるのですよね…．

Re: 中心力

mNeji さんのレス (2006/07/19(Wed) 01:42)

p8に出てくる「r」は，p10の右側の黄色い丸(事実上の太陽)から右上にある青い丸(地球)とを結んだ線分の長さです．

これらの2つの黄色い丸は楕円軌道の「焦点」であり，座標原点「O」と明らかにことなってませんか？

p13の「太陽の絵」と赤い線(楕円軌道)との関係をようく眺めてくださいね．

Re: 中心力

ta さんのレス (2006/07/19(Wed) 01:42)

rもθもtの関数として考えるのでしょうか…？

Re: 中心力

ta さんのレス (2006/07/19(Wed) 01:47)

なるほど…確かに楕円の焦点ですよね．それでは(3)はどう処理したらよいのでしょうか…少しこんがらがってきました……

Re: 中心力

yama さんのレス (2006/07/19(Wed) 02:45)

>rもθもtの関数として考えるのでしょうか…？

そのとおりです．

>なるほど…確かに楕円の焦点ですよね．それでは(3)はどう処理したらよいのでしょうか…少しこんがらがってきました……

確かに万有引力のような距離の-2乗に比例する引力による運動は力の中心を焦点とする楕円運動になりますね．（双曲線になることもありますが・・・） しかしこれ以外にも楕円運動になる場合があります．それは１点からの距離に比例する引力がはたらく場合です．ただし，この場合の楕円は力の中心を焦点とする楕円ではなく，力の中心が楕円の中心になります．これは空間振動子（三次元振動子）といわれるものです．

Re: 中心力

mNeji さんのレス (2006/07/19(Wed) 11:13)

>(2)の後半の式が分かりそうで分からないのですが…．普通の極座標と同じでx=rcosθ,y=rsinθと考えるのですよね…．

>rもθもtの関数として考えるのでしょうか…？

>確かに楕円の焦点ですよね．それでは(3)はどう処理したらよいのでしょうか…少しこんがらがってきました…

これらは，taさんの心の中では，一連の疑問を構成していると思います．恐らく，私も始めて「ケプラーの法則」を式で説明できると聞いて興奮したものの，なかなかすんなり来ませんでした．特に，角度θを時間の関数として解く，「ケプラー方程式」の話を友人から聞くまでは，スッキリしませんでした．

で，これらの疑問を個別に論議すると，複雑な関係になってしまうので，とりあえず私からみた疑問点を軸に説明してみます．

【説明1】運動方程式：接線方向と動径方向

問題の式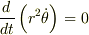； \frac{d }{dt} \left(r^2 \dot \theta\right)=0

は，時間に依存した式 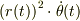\left(r(t)\right)^2\cdot \dot \theta (t) が時間微分されるとゼロになる，従って，その式全体を時間で積分すれば定数になる，と考えます．

高校で訳もなく，円運動ばかりやらされた身とすれば，だから「r=一定では？」と思われるのでしょうが，残念なことに違うのです．

上記で積分した式を，「面積速度一定」で，ケプラーの第..法則ですね． しかし，方程式の意味は；

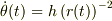
\dot \theta (t) = h \left(r(t)\right)^{-2}

とかける事です．左辺は角度だけ，右辺は動径半径r(t)だけの式です．これを最初の式，動径方向の微分方程式に代入すると，r(t)だけの微分方程式が得られます．これを解ければ，目出度いのですが初等関数では解けないのです．これは物理数学で特殊関数，わけてもベッセル関数を知る必要があります．

勿論，ニュートンさんの時代では，そんな便利な数学ツールは用意されていないので，r <-> t の関係を求めないで，r <-> θ の関係に持ち込むようにしたのです．

それが 「p9」にさらっと書いてあるのです．時間があれば，解析力学の教科書を見るか，自分でp9をにらみながら，どのようにしてdt→dθに換えていくかフォローしてください．なんでp9の最後の式に赤いフレームを付けたくなったか判るとおもいますよ．

さて，この式が意味する軌道の一つ，楕円についてはp10を見てください．