チャパ さんの書込 (2006/07/18(Tue) 18:34)

荷電粒子の運動方程式がどうしても導けないのですがだれか，はじめの式でいいので教えてくれませんか？私が思うに， 電界と磁束密度を反対称共変テンソル場，f^（μν）で表し，4元電流をj^μで表し，テンソル密度を大文字で表すと定義し，ただしXを局所ローレンツ系を示すものとしたら，

md^2X^μ/dτ^2＝F^（μν）（X）J_ν（X）

と思ったので，この式から一般座標に変換計算していったのですがどうしても答えが合いません，計算は合っていると思うので多分上の式（はじめの式）が間違っていると思うのですが，どうなのでしょう？この式は合っているのでしょうか？

mNeji さんのレス (2006/07/18(Tue) 19:17)

はじめまして．

こんな文を携帯で書いてるって，信じられませんが(笑)．

大昔，電磁気のなかで，相対論的な古典粒子(電磁場+ローレンツ力)をやったぐらいで，その上，手持ちに物理の本はないのですが...

この初めの式は何と言う本の何ページに記載されていましたか？

式をTeXにして見ます

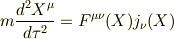
ここで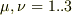

===＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 参考までに，下の<_tex>や</_tex>からアンダスコアをとればTeX表示になりますよ．

<_tex> mfrac{d^2X^mu}{dtau^2}=F^{mu nu}(X)j_nu(X) <_/tex>

式の部分は英数しか許されないようなので，携帯ではこのtexの方が早かったりして．

ここで<_tex>mu,nu =1..3</_tex>

チャパ さんのレス (2006/07/18(Tue) 20:03)

お初ですmNejiさん(^O^)／ チャパパパパ（爆笑） はいはい，携帯で数式を書くなんて無謀ですね（笑）でも残念ながら携帯でしか見れないのでTexが文字化けしてしまうんですよ〜(>_<．) でパソコンなどの知識がないのですがアンダスコアって何ですか？

それで本は『一般相対性理論（内山龍雄）』なんですけどこの本のP112がわからないんです．後，荷電粒子の電磁場および重力場の全作用積分がなんであんな形になるかも分かりません(>_<．)この式は，の本のｐ116にのってます．

少しでもいいので何かおぼえている教えてください．m(__)m

mNeji さんのレス (2006/07/18(Tue) 20:24)

私は学生の時，砂川さんの理論電磁気学一辺倒だったのですが，この内山さんは砂川さんのお師匠さんだったそうです(知人からの伝聞)．

その人に拠れば，内山さんは電磁気でも良い本を書かれているのに，そんな事も知らなかったのか...言われました．

私自身は，流体力学の勉強中なので，相対論までは手がまあらないので，近くの図書館に在れば眺めてみます．

従って，この分野に詳しい方，おっ，少なくともお一人は...，にコメントをお願いいたします．ペコリ．

mNeji さんのレス (2006/07/18(Tue) 20:54)

すこし感じを知るためにインターネット検索をして見ました：

yahoo:[共変形式 マクスウェル方程式]

1. 相対論part2 * http://members.jcom.home.ne.jp/1228180001/whats%20tensor20.htm 2. 運動方程式の共変形式 * http://takaosuda.hp.infoseek.co.jp/homepage/relate/ap4.html 3. 運動物体中の電磁気学 * http://www4.ocn.ne.jp/~okabek/relativistic-em/node5.html

ここらを見ることはできますか？

チャパ さんのレス (2006/07/18(Tue) 21:10)

すげぇぇぇえぇ〜！！！(￣□￣;)!! 自分は内山龍雄さんのファン何ですよ(^O^)／いままでいろんな一般相対論の本を探していたけど，これほどいい一般相対論の本がないくらい，感動させられている本なんですよ(^O^)／と言うか今まで読んできた全ての本の中でも，私の中で一番の本なんですよ（笑）

こんな形で（mNejiさんを通して）少しでも関わりがもてたことを誇りに思います（笑）

チャパ さんのレス (2006/07/18(Tue) 21:17)

チャパパパパ(￣□￣;)!!残念ながら見ることはできませんでしたが，今度インターネットのできるお店に行って見てみようと思います．mNejiさんありがとうございます．

toorisugari no Hiro さんのレス (2006/07/18(Tue) 21:38)

> 後，荷電粒子の電磁場および重力場の全作用積分がなんであんな形になるかも分かりません(>_<．)この式は，の本のｐ116にのってます．

この式は通常の電磁気学(特殊相対論)の中での電磁場＋粒子の作用積分に相当するものです．式をTeXで書こうかと思いましたが，referenceだけにしておきます．

砂川重信「理論電磁気学」P.413 ランダウリフシッツ「場の古典論」P.51

(以下うろ覚え注意報) ローレンツ力やクーロン力を「粒子のラグランジアン中の運動量＋A」で表現できることを「発見」したのはDiracで，このあたりが"minimal interaction"と呼ばれる理論です． (うろ覚え注意報終わり)

お尋ねの式は上の式，あるいはそれを変分したものを一般座標変換に対して共変な形にしただけですね．

チャパ さんのレス (2006/07/18(Tue) 22:11)

ぉお・・・うる覚え注意報が発令されましたなぁー(￣〜￣)ξ

ありがとうございます，明日図書館で，通りすがりのヒロさんが紹介してくれた本を探してみますね(^O^)／，ってもう通りすがってるか・・・

チャパ さんのレス (2006/07/18(Tue) 22:21)

通りすがりのヒロさんまだいますか〜(￣□￣;)!!

さっきコメントを見落としていたのですが，あの式で合っているのですか？

と言うことは右辺がテンソル密度でも，左辺がテンソル密度でなくてもいいのでしょうか？

mNeji さんのレス (2006/07/18(Tue) 22:34)

>チャパパパパ(￣□￣;)!!残念ながら見ることはできませんでしたが，今度インターネットのできるお店に行って見てみようと思います．

最近では，携帯にキーボード付きで，数万円で買えるそうですが．

>ローレンツ力やクーロン力を「粒子のラグランジアン中の運動量＋A」で表現できることを「発見」したのはDiracで，このあたりが"minimal interaction"と呼ばれる理論です．

本当に，ディラックさんは，良い所取りしてますよね．気分は，ちぇ，チェ，ちぇ．

ニュートン，マクスウェル，ディラック，ペンローズと英国学派の伝統を感じます．

チャパ さんのレス (2006/07/18(Tue) 22:53)

ディラックって言ったら，デルタ関数くらいしか知らないや（笑）

この掲示板のしたに携帯用改造ってあるんですが，それをやると携帯電話でも普通に文字化けせずにテンソル表示など見れるのでしょうか？

toorisugari no Hiro さんのレス (2006/07/18(Tue) 23:08)

> さっきコメントを見落としていたのですが，あの式で合っているのですか？ > と言うことは右辺がテンソル密度でも，左辺がテンソル密度でなくてもいいのでしょうか？

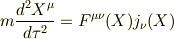
これですか？微妙にちがうような．

先に挙げた「バコテン」P68(23.4)式には

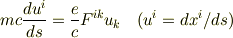
(mcfrac{du^i}{ds}=frac{e}{c}F^{ik}u_{k}quad(u^i=dx^i/ds)) と書いてある．

最初の式の左辺にも密度量をかけなきゃだめですね． でも，さて，(23.4)の両辺にディラックのデルタ関数 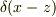をかけても共変なのだろうか?謎．

yama さんのレス (2006/07/19(Wed) 00:05)

「バコテン」はガウス単位系で書いてありますが，SI単位系では mdu^μ/dτ＝eF^(μν)u_ν（u^μ=dx^μ/dτ） すなわち 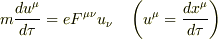になるようです．

チャパ さんのレス (2006/07/19(Wed) 00:47)

ヒロさんありがとうございます．

私の式では左辺の式にJがあるのに対しヒロさんが紹介してくれた式には代わりにu_iがあるのですが，これは速度を表しているのですか？

後，私の式では左辺に2つ密度量があるのですが，だとしたら右辺にも密度量を2つかけなくてはいけないのでしょうか？

見ての通りヒロさんの質問には答える事のできるレベルではございませんが，私の知っているかぎりディラックのデルタ関数には，簡単に書くと

δ（x−z）＝∂（x'）／∂（x）δ（x'−z'）

と言う変換則がありますよ．って，ヒロさんだから知ってたかな？

toorisugari no Hiro さんのレス (2006/07/19(Wed) 00:50)

やっぱり「うろ覚え」ではだめですね． 運動量がでるのはラグランジアンでなくハミルトニアンでしたね． あとは，詳しい人解説求む，です．

toorisugari no Hiro さんのレス (2006/07/19(Wed) 00:54)

> 携帯なのであまりよく分からないのですが，ヒロさんの紹介してくれた式との違いは，左辺にcがあるのと右辺にe/cがあるところでしょうか？

そこはyamaさんがかかれているとおり単位の問題ですから無視してもいいかと．(いけないんですけどね．)

> 後，私の式では左辺の式にJがあるのに対しヒロさんが紹介してくれた式には代わりにu_iがあるのですが，これは速度を表しているのですか？

そうです．

> 左辺に2つ密度量があるのですが，だとしたら右辺にも密度量を2つかけなくてはいけないのでしょうか？

? は密度量ではないはずです．

> 言う変換則がありますよ

そう．だから一番手軽に密度量にできるかなと．

チャパ さんのレス (2006/07/19(Wed) 01:04)

すみませんYamaさん時間差が合ったようで，いつの間にか書き込んどいてくれたようですね．すみません．

後ヒロさんにもすみません，左辺ではなく右辺に密度量が私の式では2つあるんです．なのでこの場合左辺にも2つ密度量をかけなくてはいけないのでしょうか？と言いたかったのです（笑） 速度uでしたか，もう少し考えてみることにします．

toorisugari no Hiro さんのレス (2006/07/19(Wed) 01:10)

yamaさんの式をいただきます． mdu^μ/dτ＝eF^(μν)u_ν（u^μ=dx^μ/dτ） この両辺にデルタ関数をかけ，すべての質点で和を採って ρ_e = Σ_i eδ(x-x_i) ρ_m = Σ_i mδ(x-x_i) と置き換え， ρ_m du^μ/dτ＝ρ_e F^(μν)u_ν と考えたらどうでしょう． ρ_e u_νをＪ_νと置いてもいいけど，意味あるかな?

チャパ さんのレス (2006/07/19(Wed) 01:41)

ん〜・・・ヒロやんやヤマさんの式はF^μだけがテンソル密度に見えるのですが，違うのでしょうか？

toorisugari no Hiro さんのレス (2006/07/19(Wed) 01:48)

??? Fもuも密度量ではないですよ．チャパさんの式ではJだけが密度量ですね．

yama さんのレス (2006/07/19(Wed) 02:05)

mdu^μ/dτ^＝eF^(μν)u_ν の F^(μν) は単なる電磁場テンソルであって，テンソル密度ではありません． Ｊ_ν は電流密度ですが，これはベクトルであって，一般相対論でいう密度量ではないと思います．

toorisugari no Hiro さんのレス (2006/07/19(Wed) 02:06)

> F^μだけがテンソル密度に見えるのですが > Fもuも密度量ではないですよ dual tensorと混同していませんか?

toorisugari no Hiro さんのレス (2006/07/19(Wed) 02:15)

> Ｊ_ν は電流密度ですが，これはベクトルであって，一般相対論でいう密度量ではないと思います．

そうですね．ご指摘ありがとうございます． 特殊相対論で与えた式そのままではだめで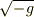， をかけて初めて密度量になるんでしたっけ．

そういう意味ではδ関数云々は的はずれぽいので無視してください．

チャパ さんのレス (2006/07/19(Wed) 02:37)

おぉ・・・みなさん，そうでしたか，私は色々と誤解していたようで・・・でもこれでスッキリしました（笑）

つまり話をまとめると密度量を使う必要はなくて，四元電流ではなく，u_νを使って縮約した指標の合計をとることによって電磁場における力が表せるわけですね． 後はこの式を一般座標変換すれば求まる，と言うことですか． みなさん大変有難うごさいました．