疎密波

変位の正の向きを，縦波の進行方向の向きとします．速さが最大となる点とは？と聞かれたら，右に?t（一瞬）秒間進んだとき，変位（縦軸）が大きく変化する点を答えればいいのではないでしょうか？図ではうすい灰色で，右に移動した波を描いています． ?t秒後のグラフを右に動かしましたが，疎密波は右に進んでいるので，疎な点や密な点が右に動いてゆくことをイメージして，了承されるかと思います．グラフから，バネなどの縦波のイメージを読み取ってください．

例えば，点ｇの付近を見てください．少し怪しい図ですが，変位が最大にみてとれると思います．．．速度＝変位／?ｔから速さが最大になると思います．変位が＋なので，速度ベクトルは右向きの方向です．他の点も調べてみてください．同様に，速度０な点を探してみてください（変位が最も小さい点）

Re: 疎密波

サンダさんのレス (2006/07/16(Sun) 10:54)

早速の返信どうも有難うございます．

グラフはChappyさんの書いてくださったものがまさにそのままです．

速度を見る場合はちょっと進んだグラフを書いて変位の大きさと向きの変化で見る．ということで．納得です．元のグラフばかり眺めてたから出来なかったんですね．

グラフを見ると速度０の点は変位最大の点のようですね．変位最大＞次の瞬間逆に変位し始める＞つまりは停止しているという解釈でもいいでしょうか．

すごく分かり易かったです．どうもありがとうございました．

Re: 疎密波

Chappy さんのレス (2006/07/16(Sun) 11:03)

ご理解していただけたようで何よりこちらも嬉しいです．．．

速度０の点も，サンダさんのおっしゃるとおりですよ．動かす前に変位最大にある点が，グラフを少し動かしてみると，ほとんど変位に変化はないですね．変位の変化が十分小さいので，その点は速度０という解釈でいいと思います．雰囲気は二次関数のグラフなどの極大・極小のイメージでしょうか．まさに接線の傾き（速度）が−→０→＋などと変化します．

とはいっても，この問題，高校時代の僕も苦手でしたよ．．．

Re: 疎密波

mNeji さんのレス (2006/07/16(Sun) 16:03)

Chappyさん：

グラフは判り易かったです．高校では式では表現しませんか？

例えば，粗密波の進行方向に向いて正に変位をとり，ある時間の変位は

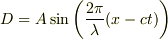
$D = A\sin\left(\frac{2\pi}{\lambda}(x-ct)\right)$

ある微小時間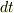に変わる変位の変化量

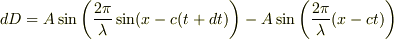
$dD = A\sin\left(\frac{2\pi}{\lambda}\sin(x-c(t+dt)\right) - A\sin\left(\frac{2\pi}{\lambda}(x-ct)\right)$

三角関数の展開ができれば，等々．

でも，こんな細かいことを高校生に教えるメリットて何でしょうかね．

Re: 疎密波

Chappy さんのレス (2006/07/16(Sun) 16:58)

確かに，波の式をちゃんと三角関数などで表すことをしました，少なくとも僕の時代では．それでも，おおっぴらに加速度を微分で求めようなどとはしませんね．教科書には結果が書いてあって，配慮として，図で幾何的に説明してます．僕の物理の先生は微分する，とはっきり言いましたが．さらには，今の教科書（といっても，たった３年新しい教科書ですが）からはほぼ消えているようですよ．

そもそも物理で，微分積分が使われていることを認識している高校生はどれほどいるのでしょうか？僕の持っている教科書には微分という言葉は載っていません．

大学と高校の物理のギャップが少し大きいと思います．

Re: 疎密波

mNeji さんのレス (2006/07/16(Sun) 17:24)

解説有難うございます．高校の物理と数学は，なにかアンバランスですね．教えるべきものを教えないで，一方で変に技巧的であったり．

ところで，今回の図はとても素晴らしいと思いますが，いっその事，物理のかぎプロジェクトに参加されませんか？

Re: 疎密波

Chappy さんのレス (2006/07/16(Sun) 18:31)

お誘いありがとうございます．大変嬉しいです．ただ，僕には，こと数学に関しては未熟なので，お力になれるか分かりません．物理は高校までしか知りません．それでも，数学の人間が受け入れられるのならば，物理のかぎプロジェクトに参加してみたい気持ちはあります．

実は３，４年ほど前から物理のかぎしっぽというサイトを知っていて，物理のかぎしっぽみたいな，数学のサイトがあったらいいなぁなんて考えて，自らサイトを立ち上げようと，大それたことを考えた時期もありました．学部生活が忙しくて頓挫しましたが（笑）数年前から数学に関する記事が増えてきて，物理関係の方の数学感みたいなものが垣間見れるのがおもしろいです．これからも，ご活躍期待しております．

Re: 疎密波

Joh さんのレス (2006/07/16(Sun) 20:30)

数学専門の方に入っていただけると，心強いです．

[home] [掲示板] [ページの先頭]