流体問題
流体問題
k・k さんの書込 (2006/07/15(Sat) 23:06)
今,流体を学んでるものなんですけど, 非圧縮,粘性で,2次元流れにおいて,速度u=2xy,v=x^2−y^2+1のとき, 1この流れが連続方程式を満たすことをしめせ. 2渦なしの条件を満たすことをしめせ. 3速度ポテンシャルをもとめよ 4流れ関数をもとめよ
という問題なんですが,1番から,どう証明したらいいか分からないので,教えてください.
Re: 流体問題
mNeji さんのレス (2006/07/15(Sat) 23:58)
始めまして.
大学生さんですよね.私も,これから「非圧縮,粘性」で水泳の解析をするために勉強をしようとしていますので,一緒に考えたいと思います.
今速度場が与えられている;
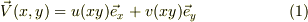
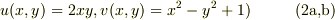
ベクトル解析は既に習いましたか? とりあえず,1について考えましょう.いま,直ぐ手元にある「連続流体物理学,西川 恭治,大林 康二,若谷 誠宏・共著,朝倉書院,1981-04」を見ながら説明します.
- 連続の方程式(the equation of continuity)
一般的には,密度を  とすると
とすると
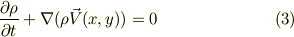
ですが,非圧縮の為に  は時間微分も空間微分もゼロですから,
は時間微分も空間微分もゼロですから,
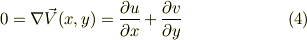
ここで(2)を上式の右辺に代入すると;
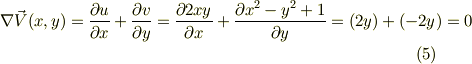
と上式は常に「連続の式 (4)」を満たしている.
- 渦なし運動(irrotational motion)
簡単に言えば,x,y平面に垂直なz軸について,流れが回転していないことを言う.これは数学的には,
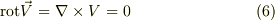
で表せる.(1)(2)より,上式を書き下すと上式のz成分は;
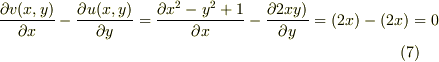
よって(1)(2)で与えられた流れは渦の無い運動である.
- 速度ポテンシャル(velocity potential)
渦の無い速度場は速度ポテンシャル  の勾配で与えられる;
の勾配で与えられる;

成分ごとに書き下せば
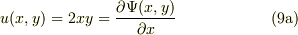
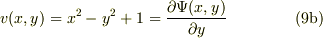
複雑な関数である(9b)をyについて積分すると,積分定数を無視して,
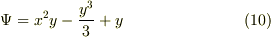
(10)を(9a)右辺に代入しても(9a)左辺に一致する.従って,(9)は(8)の速度ポテンシャルである.
- 流れの関数(stream function)
流れの関数 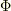 によって
によって
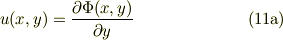
と与えられるとする.
連続の式(4)に代入し,偏微分の順序を交換できることを利用して
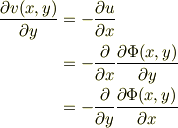
従って,左右の偏微分の中身を比較して
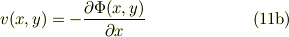
速度ポテンシャルを積分して得たと同様に(11b)をxで不定積分すれば,
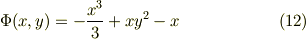
逆に,流れの関数 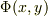 の全微分を考えると;
の全微分を考えると;
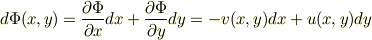
流れの関数 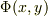 が一定の,等高線では与式は零だから;
が一定の,等高線では与式は零だから;

これは,流れの関数 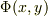 の等高線の接線は,流速場の傾きに一致していることを示す.
の等高線の接線は,流速場の傾きに一致していることを示す.
Re: 流体問題
k・k さんのレス (2006/07/16(Sun) 00:27)
返信ありがとうございます.ベクトル解析は,まだなのですが.教科書には,連続の式は,ρqA=constと習ったのですが,上の式との違いはなんですか? 後,あまりタイピングがうまくなく,数式の出し方もできなく,うまく伝えられないんですが,突然ですみませんが電話とかでは無理ですか?
Re: 流体問題
mNeji さんのレス (2006/07/16(Sun) 00:52)
お使いの教科書のISBNは判りますか?
ベクトル解析の知識が無い前提で,今の問題を解くのは事実上無理だと思います.
電話ではますます混乱するばかりと思います.
逆に,急ぐのならば,回答を書いて見たらどうですか.
>非圧縮,粘性で,2次元流れにおいて,速度u=2xy,v=x^2−y^2+1のとき,
といった感じで良いですから.ただし全角だと,全て書き換えなので,英数モードで入力してください.
Re: 流体問題
k・k さんのレス (2006/07/16(Sun) 01:07)
ISBNとは,なんですか?後,1番は省略されてて,2番はx^2y^2-y^3/3+y 3番は,xy^2-x^3/3-xです.uを積分すれば出ると思ってたんですけど値が合わないのですが .
Re: 流体問題
mNeji さんのレス (2006/07/16(Sun) 01:30)
ISBNは本に付いているある種の連番ですが,不要です.
偏微分は判りますか? 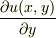 は,u(x,y)で,xは変わらないとして,yで微分することです.
は,u(x,y)で,xは変わらないとして,yで微分することです.
多分,1,2が省略されていて,2,3が書かれているのだと思います.
私には,ベクトル解析が出来ない限り,これらを解くことは出来ないと思います.これをご覧になっている方で,解説できましたら宜しくお願いします.
私は,通常のベクトル解析に従って回答を作成したいと思います.(No.10554 に追加の予定)
Re: 流体問題
k・k さんのレス (2006/07/16(Sun) 01:37)
わかりました.なんとか自分でやってみます.ありがとうございました.
Re: 流体問題
mNeji さんのレス (2006/07/16(Sun) 04:38)
この問題は,良く出来ていて,お陰さまで速度ポテンシャルと流れの関数との役割を理解し易くなりました.
なお,速度ポテンシャルについては,「gradをつかう問題について:2006/07/12(Wed) 22:57 No.10439」に,速度ポテンシャル 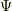 のgradが速度勾配に対応する簡単な説明があります.
のgradが速度勾配に対応する簡単な説明があります.
是非とも,これを機会にベクトル解析を勉強してください.
この次のステップに複素ポテンシャルが
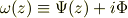
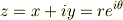
を使うと解析的な計算が効率よく出来るようです.
渦の運動は,もう少し先のようですが....お互い,頑張りましょう.