波動方程式の一般解
波動方程式の一般解
とーしろ さんの書込 (2006/07/15(Sat) 00:56)
はじめまして. 量子化学の勉強を始めた企業研究員です. 物理は苦手なので,皆さんの知識で手助けしてください.
テキストを見て波動方程式を変数分離して偏微分方程式を,
常微分方程式 d^2X(x)/dx^2=λX(x) d^2T(t)/dt^2=c^2λT(t)
となることは理解できました.しかし,そのあといきなり一般解が X(x)=Acos(x(-λ)^1/2) + Bsin(x(-λ)^1/2)/(-λ)^1/2 T(t)=Acos(t(-c^2λ)^1/2) + Bsin(t(-c^2λ)^1/2)/(-c^2λ)^1/2
と出てきます.どのように一般解を導くのか,ご教授願います. よろしくお願いします.
出展 C.W.Wong著 小林てつ(さんずいに育攵)郎・近匡訳 40ページ式(4・98)
Re: 波動方程式の一般解
toorisugari no Hiro さんのレス (2006/07/15(Sat) 01:09)
> どのように一般解を導くのか,ご教授願います.
どちらで躓いておられるのでしょうか?
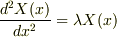 の
の  が何故負の数となるのかわからない.
が何故負の数となるのかわからない.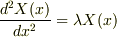 の解き方そのものがわからない.
の解き方そのものがわからない.
Re: 波動方程式の一般解
とーしろ さんのレス (2006/07/15(Sat) 01:12)
toorisugari no Hiro様
返信ありがとうございます.
(2)の解き方そのものがわからず,困っております.
説明不足で申し訳ありませんでした. どうぞよろしくお願いします.
Re: 波動方程式の一般解
Re: 波動方程式の一般解
とーしろ さんのレス (2006/07/15(Sat) 01:27)
CO様
返信ありがとうございます.
リンクを見させていただきました. しかし,(5)から(6)への変換がわからないのです. 何がわからないというと, 1.なぜf(x)=ae^axを代入するのか 2.代入する式がなぜf(x)=ae^axなのか の二点です.
勉強不足な私ですが,どうぞよろしくお願いします.
Re: 波動方程式の一般解
Re: 波動方程式の一般解
Re: 波動方程式の一般解
Joh さんのレス (2006/07/15(Sat) 03:18)
自然対数の底  は,
は, 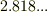 というおかしな数です.そもそも何でこんな数を考えたというと,微分しても元と変わらず,
というおかしな数です.そもそも何でこんな数を考えたというと,微分しても元と変わらず, 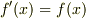 を満たす関数を考えてみたら,
を満たす関数を考えてみたら, 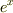 がどうやらそういう関数になりそうだということが分かったからです.(このような明らかな動機がなければ,こんな変な数を思いつくことはないでしょう.もっとも,
がどうやらそういう関数になりそうだということが分かったからです.(このような明らかな動機がなければ,こんな変な数を思いつくことはないでしょう.もっとも,  は数学の色々な場面に顔を出す大事な数ですが,いま
は数学の色々な場面に顔を出す大事な数ですが,いま  の話に深入りすると脇道に逸れるのでやめます.)
の話に深入りすると脇道に逸れるのでやめます.)
では,なぜ 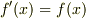 を満たす関数を知りたかったかと言えば,そんな関数を知っていれば微分方程式を解くのに便利だからです.
を満たす関数を知りたかったかと言えば,そんな関数を知っていれば微分方程式を解くのに便利だからです.
いきなり 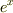 を代入するのを見て,意味が分からなかったかも知れませんが,
を代入するのを見て,意味が分からなかったかも知れませんが, 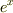 の生い立ちを考えてみれば,これはトリッキーな解法というよりは,むしろ
の生い立ちを考えてみれば,これはトリッキーな解法というよりは,むしろ 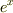 の定義そのものです.
の定義そのものです.
Re: 波動方程式の一般解
toorisugari no Hiro さんのレス (2006/07/15(Sat) 03:23)
Johさん....あの....1行目の定数.....
Re: 波動方程式の一般解
とーしろ さんのレス (2006/07/15(Sat) 04:05)
toorisugari no Hiroさんがあげた一階微分方程式をよく見ると f(x)を2回微分しても,元の関数f(x)のλ倍になっている ことから,微分しても元の関数と変わらない f(x)=e^axを代入して解を求める このような解釈で正しいのでしょうか?
Re: 波動方程式の一般解
toorisugari no Hiro さんのレス (2006/07/15(Sat) 04:12)
> 微分しても元の関数と変わらない
変わらないというのは語弊があります( 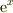 のときのみですね.)が,考え方は間違っていません.
のときのみですね.)が,考え方は間違っていません.
1階微分して元の関数の定数倍になるような関数 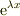 (
(  は任意の定数)を2階微分方程式(「2階微分して元の関数の定数倍になるような関数をもとめよ」)の解の候補と考えるのは自然ですよね.
は任意の定数)を2階微分方程式(「2階微分して元の関数の定数倍になるような関数をもとめよ」)の解の候補と考えるのは自然ですよね.
Re: 波動方程式の一般解
Joh さんのレス (2006/07/15(Sat) 04:45)
>Johさん....あの....1行目の定数.....
あ,2.718...ですね.お恥ずかしい.しかし,みなさん夜遅くまで起きていらっしゃいますね!
とーしろさん,
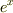 を利用する基本的な考え方はだいたい合っています.あとは定数や符号に気をつけてください.もうすぐ,この解がごく自然に思えてくると思います.
を利用する基本的な考え方はだいたい合っています.あとは定数や符号に気をつけてください.もうすぐ,この解がごく自然に思えてくると思います.
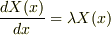 は解けますか?
わからなければ
は解けますか?
わからなければ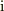 を虚数単位として,
を虚数単位として, 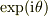 が何を表すかご存じでしょうか?
が何を表すかご存じでしょうか?