問題に文字が与えられていないのに・・・

えりさんの書込 (2006/07/13(Thu) 16:36)

こんにちは．来年大学受験の高卒生です．次の問題には重力加速度gが与えられていないのですが，最終解答にgが使われていました．

「水平な天井の一点Ｏからつるされた長さl，質量mの振り子がある．振り子の最低点Ｂから高さｈの点Ｃには，釘が打ってあるとする．振り子は鉛直線から角度θの点Ａから静かに離して振らせるとする．糸の張力Ｓは最低点Ｂを通るときに，どれだけ変わるか．」

そして解答は2mg(1-cosθ)(l/h-1)となっていました．

本当の答えは何なのでしょうか…教えて下さい．

Re: 問題に文字が与えられていないのに・・・

CO さんのレス (2006/07/13(Thu) 16:57)

えりさん，こんにちは．

> 最終解答にgが使われていました．

この最終解答とは何を指しているのでしょうか．問題集の解答？友達の解答？先生の解答？

B点に達する直前の張力を 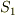S_1 ，B点に達した直後の張力を 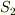S_2 とすると，上では差

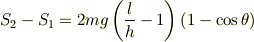
$S_2-S_1=2mg\left(\frac{l}{h}-1\right)\left(1-\cos\theta\right)$

をとっているようですが，比

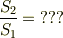
$\frac{S_2}{S_1} = \text{???}$

をとってやれば重力加速度を用いずに，どれだけ変化するかを示せるのではないでしょうか． ??? は自分で計算してみてくださいね．

Re: 問題に文字が与えられていないのに・・・

mNeji さんのレス (2006/07/13(Thu) 18:44)

えりさん：

はじめまして．

振り子が最低点に来て，釘にぶつかる瞬間の前後での糸の張力の差分を出そうとすると，どうしても重力加速度gはいるとおもいます．

質問に「重力加速度をなになにする」という文章が無ければ，あまりいい問題ではありませんね．

でも，本当に知りたいのは，そのことだけですか？たとえば，釘にぶつかる前後の遠心力をどう考えるとかは良く判りますか？

Re: 問題に文字が与えられていないのに・・・

えりさんのレス (2006/07/13(Thu) 18:44)

>この最終解答とは何を指しているのでしょうか．問題集の解答？友達の解答？先生の解答？

先生の解答です．

比で自分で計算してみました．Ｓ2=ｌ/ｈ*Ｓ1となったので，どれだけ変化したか聞かれていることに対しては，l/h倍変化した，と答えればいいのですね！

Re: 問題に文字が与えられていないのに・・・

えりさんのレス (2006/07/13(Thu) 18:51)

mNeji様

何とかこの問題に関しては向心方向の運動方程式は立てられました… ですが，円運動をマスターしているとは到底言えないレベルです．．

Re: 問題に文字が与えられていないのに・・・

mNeji さんのレス (2006/07/13(Thu) 19:37)

えりさん：

この問題は，変哲の無い問題に見えますが，とてもトリッキーな問題なのだと思います．そもそも，運動方程式を計算する準備のない高校生に向けて教えることではないと思っています．

さらに高校でどのように教えているのか知りませんが，予想で書いてみます．おかしければ他の人が教えて下さると思います．

推定ですが，重力エネルギーの保存則は使えるのだろうと思います．すると，振り子の重りが最下点Bに来た時の水平方向の速さvは出せるとします．

糸がCにぶつかる前後で，水平方向の速さvは変わりません．しかし，重りが振られる糸の長さがL(小文字だと見難いので大文字)→H(前に同じ)と急変していることです．

いま，重りが最下の超近傍にいる場合を考えると，張力Sは；・S=重力+遠心力＝mg+mLω^2 ・角速度ω=v/L 従って， S=mg+mL(v/L)^2=mg+mv^2/L

糸がCにぶつかった直後の張力S'は，水平方向の速さvのままですから S'=mg+mv^2/H 差分は S'- S = mv^2(1/H-1/L)=(L/H-1)mv^2/L

ここで止めとけばgは入ってきませんが(笑)．

Re: 問題に文字が与えられていないのに・・・

えりさんのレス (2006/07/13(Thu) 19:54)

>S'- S = mv^2(1/H-1/L)=(L/H-1)mv^2/L

ここで止めとけばgは入ってきませんが(笑)．

そうすると，今度はvが与えられていないので，力学的エネルギー保存の式を用いてvを求めようとすると，gが出てきますよね…

ある意味トリッキーな感じです…

Re: 問題に文字が与えられていないのに・・・

CO さんのレス (2006/07/13(Thu) 19:56)

えりさん， mNeji さん，こんばんは．

> 先生の解答です．

先生に「問題文中に無い文字を使って解答しているが良いのか？」と質問してみましょう． :)

> 比で自分で計算してみました．
> Ｓ2=ｌ/ｈ*Ｓ1となったので，どれだけ変化したか聞かれている
> ことに対しては，l/h倍変化した，と答えればいいのですね！

考え方はあっていますが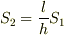， $S_2 = \frac{l}{h} S_1$ という結果は正しくないと思います．

mNeji さんの求めた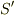，をもとにして，エネルギー保存則

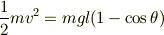
$\frac{1}{2}mv^2 = mgl(1-\cos\theta)$

を用いて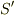， , の比をとれば正しい結果が得られると思います．最後は比で答えるのが妥当だと思います．

Re: 問題に文字が与えられていないのに・・・

えりさんのレス (2006/07/13(Thu) 21:21)

つまり，比の形を崩してはいけないということですね（＾＾）どうもありがとうございました．

[home] [掲示板] [ページの先頭]