gradをつかう問題について
gradをつかう問題について
AI さんの書込 (2006/07/12(Wed) 18:24)
学校で以下のような問題をやりました. 「海の中で怪我をして血液が流れ,その濃度がe^−(x^2+4y^2)で与えられる.点(X0,y0)にいるサメは濃度の濃い点をたどって近づくとすると どの方向から人に近づくか.」 という問題です.
gradU=-2xe^−(x^2+4y^2)i−8ye^−(x^2+4y^2)j gradU//dr を考えて dx/-2xe^−(x^2+4y^2)=dy/−8ye^−(x^2+4y^2) あとはこれを解くのですが 式の立て方とgradU//dr の意味がわかりません. もしわかる方がいれば教えてください.よろしくおねがいします.
Re: gradをつかう問題について
toorisugari no Hiro さんのレス (2006/07/12(Wed) 18:43)
これは一次元に広がった深い水路での話でしょうか(  は水路方向,
は水路方向,  は深さ方向).
は深さ方向).
拡散係数が水平方向と鉛直方向で違うのですね.
鮫は濃度の濃い方向をたどるのですから,  の等濃線に垂直にたどると考えればいいのでは?
の等濃線に垂直にたどると考えればいいのでは?
つまり,原点から  の角度で出発して等濃線に垂直にたどる軌跡の方程式をまずたて,次に,
の角度で出発して等濃線に垂直にたどる軌跡の方程式をまずたて,次に, 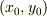 を軌跡が通るような
を軌跡が通るような  をもとめるわけです.
をもとめるわけです.
あるベクトルが等濃線に垂直ならそのベクトルは 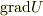 とどんな関係にありますか?
とどんな関係にありますか?
Re: gradをつかう問題について
mNeji さんのレス (2006/07/12(Wed) 19:09)
横から失礼します.
平面の原点(x,y)=(0,0)で怪我をして,濃度分布がe^云々の時,平面(x0,y0)に来た鮫が云々とも取れませんか?
Re: gradをつかう問題について
AI さんのレス (2006/07/12(Wed) 19:17)
無知でほんと申し訳ないのですが,拡散係数とはなんでしょうか. >Uの等高線に垂直にたどると考えればいいのでは? 意味がよくわからないのですが.なぜgradを使うのでしょうか. gradの意味は勾配と習ったのですが,意味というかどういうときに役に立つのか みたいなことがよくわかりません.つまりgradを理解するための問題がこれだったわけで. >あるベクトルが等高線に垂直ならそのベクトルはgradUとどんな関係にありますか?内積が0とかそういうことですか?
Re: gradをつかう問題について
AI さんのレス (2006/07/12(Wed) 19:18)
mNejiさんの問題の解釈のしかたで説明していたようにおもいます.
Re: gradをつかう問題について
toorisugari no Hiro さんのレス (2006/07/12(Wed) 19:30)
> 平面の原点(x,y)=(0,0)で怪我をして,濃度分布がe^云々の時,平面(x0,y0)に来た鮫が云々とも取れませんか?
濃度分布が
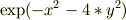
と分布が 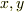 で非等方なので,通常こういう拡散係数の非等方性は水平と鉛直の場合が多いからです.ま,数学の問題ですから,背景はどうでもいいんですけど.
で非等方なので,通常こういう拡散係数の非等方性は水平と鉛直の場合が多いからです.ま,数学の問題ですから,背景はどうでもいいんですけど.
楕円状の山の途中から球を転がすときの軌跡の問題ですよね.
> 拡散係数とはなんでしょうか
インクを水に落としたときそれがにじんで広がりますが,その広がり方の度合いです.
Re: gradをつかう問題について
toorisugari no Hiro さんのレス (2006/07/12(Wed) 19:44)
> gradの意味は勾配と習ったのですが
大きさは勾配ですが,ベクトル量ですから方向と向きをもっています.この方向は?
Re: gradをつかう問題について
mNeji さんのレス (2006/07/12(Wed) 20:04)
toorisugari no Hiroさん:
>通常こういう拡散係数の非等方性は水平と鉛直の場合が多いからです.ま,数学の問題ですから,背景はどうでもいいんですけど.
しかめっつらしているお顔が見えるようです.
もしも xが海岸に平行な方向で,yが沖に向かった方向の座標とすれば,仮に拡散係数が一定でも,y方向にいくと水深が深まる分だけ見掛け上の拡散速度が速まるとか.
でも,出題側も,ある程度の背景を説明して欲しいですね.
AIさん:
私は,この質問を拝見した時,問題が完全に示されていないような気がしたので答えませんでした.(最近,ずる賢くなってきたので:笑)
でも,toorisugari no Hiroさんのように,好意的に解釈できて,かつ洞察力の深い回答者はさらなる現象を考察してしまうのです.
ですから,回答者の方をがっかりさせない為に,質問する時は「出された問題に出来る限り忠実に質問されるように,お願いします.」
ところで >>あるベクトルが等高線に垂直ならそのベクトルはgradUとどんな関係にありますか?内積が0とかそういうことですか?
とありますが,講義ノートや講義の本にはどう書いてありますか? むしろここも含めて質問するなら,二重の質問ですよね?
Re: gradをつかう問題について
toorisugari no Hiro さんのレス (2006/07/12(Wed) 20:10)
> しかめっつらしているお顔が見えるようです.
(^^;)
> もしも xが海岸に平行な方向で,yが沖に向かった方向の座標とすれば,仮に拡散係数が一定でも,y方向にいくと水深が深まる分だけ見掛け上の拡散速度が速まるとか.
ぽんと膝を打ちかけましたが,これだと  の正負で濃度がかわるので中心がずれていきませんか?
の正負で濃度がかわるので中心がずれていきませんか?
Re: gradをつかう問題について
mNeji さんのレス (2006/07/12(Wed) 20:27)
>これだとyの正負で濃度がかわるので中心がずれていきませんか?
だから完全な形で質問を拝見したいのですが...
私の想像では,怪我したのは海岸べり(0,0)なんだろうと推測しています.映画ジョーズでも,鮫は海岸に来るのでは?
#私は,数年間,ボーッとして生活して,脳内のかなりの記憶がリセットされた為か,変に裏読みが長けてきました.一種の老人力かも(笑).
Re: gradをつかう問題について
AI さんのレス (2006/07/12(Wed) 20:58)
gradU=-2xe^−(x^2+4y^2)i−8ye^−(x^2+4y^2)j のようにかけるのでベクトル2xe^−(x^2+4y^2)iとベクトル−8ye^−(x^2+4y^2)j を合成したものが方向ですか?答えになってませんか. 問題の方ですが,くわしいことは説明されていません. 上にかいた式を解いて答えがy=y0x^4/x0^4となっているだけです. なので最初の式をどのように導き出したかが知りたいのです. これから原点で怪我をしたと考えられるとおもいます.
Re: gradをつかう問題について
toorisugari no Hiro さんのレス (2006/07/12(Wed) 21:11)
> 合成したものが方向ですか?
その方向は  の等値線(等濃線)とどう関係しますかときいているんですが...
の等値線(等濃線)とどう関係しますかときいているんですが...
なぜ,その方向に 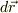 を考えるのかというAIさんの質問にこたえたいのですけどね.
を考えるのかというAIさんの質問にこたえたいのですけどね.
ともかく,いったん式が得られれば 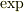 の部分はcancelするので,簡単な微分方程式になりますね.
の部分はcancelするので,簡単な微分方程式になりますね.
Re: gradをつかう問題について
AI さんのレス (2006/07/12(Wed) 21:20)
>その方向はの等値線(等濃線)とどう関係しますかときいているんですが... どのように関係してるのですか?
Re: gradをつかう問題について
toorisugari no Hiro さんのレス (2006/07/12(Wed) 21:28)
> どのように関係してるのですか?
教科書やノートにはなんて書いてありますか?
こちらとしては一緒に考えていきたいのであって,答えだけを出すつもりはありません.もし,それがご不満でしたら,私は退場します.
お役に立てなくてごめんなさい.
Re: gradをつかう問題について
AI さんのレス (2006/07/12(Wed) 21:33)
gradU//drのように書いてあるので,平行ということですか.でも意味がわかりません.
Re: gradをつかう問題について
toorisugari no Hiro さんのレス (2006/07/12(Wed) 21:41)
もう一回だけ質問します.
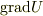 の大きさは傾きの絶対値と等しいですね.
では方向はどのような方向になっていますか?
の大きさは傾きの絶対値と等しいですね.
では方向はどのような方向になっていますか?
これがわかれば, > gradU//drのように書いてあるので,平行ということですか.でも意味がわかりません. の答えがわかります.
Re: gradをつかう問題について
Re: gradをつかう問題について
mNeji さんのレス (2006/07/12(Wed) 22:57)
おそらく,toorisugari no Hiroさんは,鮫の軌道を積分する説明文を書かれているとおもいます.
そこで,私は, 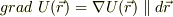 について,すこし違う角度から,考えてみます.
について,すこし違う角度から,考えてみます.
今の場合, 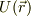 は濃度の関数ですが,こんな感じの場所の関数のことをスカラ・ポテンシャルといいます.
は濃度の関数ですが,こんな感じの場所の関数のことをスカラ・ポテンシャルといいます.
今の場合,これらの関数がある値 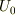 を持っている位置が
を持っている位置が
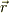 と
その近くの位置
と
その近くの位置 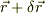 とします.
とします.
すなわち,
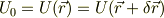
これらは,関数の値が同じ面にあるので,等ポテンシャル面といいます.右辺から中辺を引けば
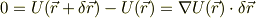
いま 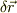 は,等ポテンシャル面の内部の変位ベクトルだから,それと内積を取るとゼロになる
は,等ポテンシャル面の内部の変位ベクトルだから,それと内積を取るとゼロになる  は,等ポテンシャル面に垂直,言い換えればポテンシャルの勾配ベクタを示すことになります.
は,等ポテンシャル面に垂直,言い換えればポテンシャルの勾配ベクタを示すことになります.
#そういう意味では,重力ポテンシャルの勾配ベクタは引力を与えます.
試験中にポテンシャル勾配が「真っ白け」となった場合は,等ポテンシャル面内での差分を思い出すと落ち着きますよ.
Re: gradをつかう問題について
mNeji さんのレス (2006/07/13(Thu) 00:03)
>2006/07/12(Wed) 21:28 No.10434
を見過ごしていたので,御免なさい.
では,代理でかんがえます.一番簡単に,準静的に濃度勾配の方向に従って鮫がうごいて来ると考えます.
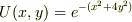
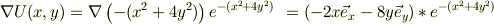
このように濃度勾配ベクタはx,yとも負の為に,濃度は中心から遠ざかるにつれて減少し,全体的にも指数関数により減衰している.
鮫の動きを(x,y)とすると,其々の位置では,その微分 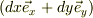 は濃度勾配ベクタに比例するので;
結局;
は濃度勾配ベクタに比例するので;
結局;
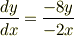
変数分離できて,
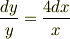
積分して
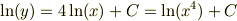
初期条件 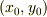 だから
だから
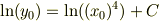
よって鮫の軌道
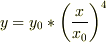
Re: gradをつかう問題について
toorisugari no Hiro さんのレス (2006/07/13(Thu) 18:20)
mNejiさんフォローありがとうございます. スレ主さんはもういらっしゃらないようですが,自分の間違いを発見したので訂正しておきます.
> つまり,原点から |2554a2bb846cffd697389e5dc8912759| の角度で出発して等濃線に垂直にたどる軌跡の方程式をまずたて,次に, |15b4ad58baaa08c32f8c67f18e672c3e| を軌跡が通るような |2554a2bb846cffd697389e5dc8912759| をもとめるわけです.
 で考えるのはまずいですね.0しかないですから.
で考えるのはまずいですね.0しかないですから.
まあ,非等方のときはある方向に偏るってのも見識かもしれないですが.mNejiさんのモデルなら沖からでなく浜に沿って,私のモデルなら下からでなく正面(横)から,襲いにくるということですか.
Re: gradをつかう問題について
mNeji さんのレス (2006/07/13(Thu) 18:55)
toorisugari no Hiroさん:
コメント有難うございます.昨日は,慌てて行き過ぎました.ペコリ.
と同時に,出題者も,きちっと出さないと,色々解釈されてしまうので大変ですね.
確かに,xを浜から海面までの距離,yを海面からの水深(鮫)までの深さと考えても,全く同じ事になりますね.
AIさんも,grad をガッチリ・マスターされますように.