suzui さんの書込 (2006/07/11(Tue) 21:30)

先程は兄の名前で投稿してしまったので削除してもう一度投稿します．

知っています．（周期）＾２/（長半径）＾３＝一定ですよね？

toorisugari no Hiro さんのレス (2006/07/11(Tue) 21:55)

できれば，おなじ スレッドに続けてほしかったのですが，，，

>（周期）＾２/（長半径）＾３＝一定ですよね？

いま，軌道が重力源を中心とする半径 の円軌道として，この一定値の値を求められますか?

重力源の質量を ，万有引力定数を 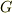，質点の質量を

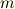
，質点の速さを として，万有引力と遠心力の釣り合いを考えます．

suzui さんのレス (2006/07/11(Tue) 22:22)

周期と長半径の値ということでしょうか？

toorisugari no Hiro さんのレス (2006/07/11(Tue) 22:28)

> 周期と長半径の値ということでしょうか？

(長)半径は としてるので，周期を求めればいいですね．円軌道の長さはわかりますから，速さを求めればいいのでは?

suzui さんのレス (2006/07/11(Tue) 22:32)

都合よくも丁度よさげな問題を見つけたので投稿してみます．

１９６９年７月アポロ宇宙船は月周回軌道を回りながら月面に着陸したＬＭが飛び立つのを待っていた．ＬＭには人類として初めて地球以外の天体に足跡をしるしたアームストロング船長が乗っていた．この宇宙船は周期約２時間で月周期をつづけていた．月の平均密度を求めなさい．ただし，宇宙船の高度は月半径に比べて無視できるものとし，万有引力定数をＧとする．また，地球や太陽による万有引力は考えなくてよいものとする．

toorisugari no Hiro さんのレス (2006/07/11(Tue) 22:46)

前の質問に答えず，新たな質問をされても困ります．ちなみに月の半径がわかりませんね．

suzui さんのレス (2006/07/11(Tue) 22:59)

ごめんなさい，惑星といってもいくつもあって具体的なものがほしかったもので・・・ 更新していなくてNO１０３８７を読む前に投稿してしまいました．

まずはこの問題の前のでお願いします．

＞(長)半径はとしてるので，周期を求めればいいですね．円軌道の長さはわかりますから，速さを求めればいいのでは? 円運動の運動方程式をたてて速さをだし，（周期）＝（２πＲ/速さ）で周期を求めればよいのですね？？

toorisugari no Hiro さんのレス (2006/07/11(Tue) 23:02)

> 円運動の運動方程式をたてて速さをだし，（周期）＝（２πＲ/速さ）で周期を求めればよいのですね？？

そうですね． それで，速さはどうなります?遠心力の計算式や万有引力の式はご存じですか?

toorisugari no Hiro さんのレス (2006/07/11(Tue) 23:04)

> ちなみに月の半径がわかりませんね．

この問題に限り不要でしたね．

suzui さんのレス (2006/07/11(Tue) 23:25)

ｍv^2/R=-GMm/R^2 からｖはもとまると思います．

> ちなみに月の半径がわかりませんね．

この問題に限り不要でしたね．

というのはどうしてでしょうか？？

toorisugari no Hiro さんのレス (2006/07/11(Tue) 23:29)

> ｍv^2/R=-GMm/R^2 > からｖはもとまると思います．

符号が違いますが，まあ，よいです．それで，先の一定値はどう表現できますか?

> というのはどうしてでしょうか？？

あわてない，あわてない．

suzui さんのレス (2006/07/11(Tue) 23:46)

v=(GM/R)^1/2なのでT=2πＲ/v=2πＲ(GM/R)^1/2 T^2/r^3=4π＾２GM/R でしょうか？

toorisugari no Hiro さんのレス (2006/07/11(Tue) 23:50)

> v=(GM/R)^1/2なのでT=2πＲ/v=2πＲ(GM/R)^1/2

おしい．途中でケアレスミスしてますよ．

suzui さんのレス (2006/07/12(Wed) 00:00)

v=(GM/R)^1/2なのでT=2πＲ/v=2πＲ(Ｒ/ＧＭ)^1/2 で，

T^2/r^3=4π＾２/GM ですね？？

toorisugari no Hiro さんのレス (2006/07/12(Wed) 00:07)

> T^2/r^3=4π＾２/GM

おめでとうございます．これにより が計算できますね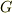． は1798年キャヴェンデッシュが鉛球実験によって地上で測定しています．

• http://ja.wikipedia.org/wiki/%E4%B8%87%E6%9C%89%E5%BC%95%E5%8A%9B%E5%AE%9A%E6%95%B0

この式は太陽と惑星の組み合わせ以外にも使え，楕円軌道にも使えるとしましょう．

さあ，あなたなら，この式を使って木星の質量をはかるのに何を観測すればよいと思いますか?

suzui さんのレス (2006/07/12(Wed) 00:14)

太陽と木星との距離でしょうか？？

toorisugari no Hiro さんのレス (2006/07/12(Wed) 00:20)

> 太陽と木星との距離でしょうか？？

違います．

は重力源の質量ですよね．そして，木星の質量を計りたいのですから，木星を重力源として起こる楕円運動を考えるのではないでしょうか?

眠たくなってきたので，そろそろ今日は終わりにさせてください．(ほかの方が手伝ってくれるかもしれませんし，解答をつづけてください．)

suzui さんのレス (2006/07/13(Thu) 21:19)

日があいてしまい申し訳ありませんでした． ＞木星を重力源として起こる楕円運動を考えるのではないでしょうか? というと，，，おそらく運動方程式を使うのでしょうから距離が必要かと思ったのですが・・・回転の速さは周期から求まりそうな気がしたので・・・

月の問題が解けました．質量と半径を文字でおき，周期と運動方程式を連立すればうまく未知数の文字が消去できました．

toorisugari no Hiro さんのレス (2006/07/13(Thu) 21:27)

>> 木星を重力源として起こる楕円運動を考えるのではないでしょうか? > おそらく運動方程式を使うのでしょうから距離が必要かと思ったのですが

と言うより，木星の質量を測定するには，どんな「天体」の運動を観測すればいいですか?って質問です．

toorisugari no Hiro さんのレス (2006/07/13(Thu) 23:10)

> 月の問題が解けました．質量と半径を文字でおき，周期と運動方程式を連立すればうまく未知数の文字が消去できました．

(^_^) 軌道半径と天体半径が一致している問題は簡単になりますね．

一応，やったかもしれませんが，確認のため，太陽の質量も計算してはどうでしょう．

地球の公転周期(1年)と公転半径(太陽中心までの距離:1天文単位=149,597,870km)から，太陽の質量もわかりますよね．

suzui さんのレス (2006/07/18(Tue) 02:08)

>，木星の質量を測定するには，どんな「天体」の運動を観測すればいいですか?って質問です． 地球ではないでしょうか？

toorisugari no Hiro さんのレス (2006/07/18(Tue) 09:06)

>> 木星の質量を測定するには，どんな「天体」の運動を観測すればいいですか?って質問です． > 地球ではないでしょうか？

地球を調べてもいいですが，元スレの質問

> 惑星の密度というのはどうやって計測しているのでしょうか？半径は計れたとしても重さは量れないですよね？？

ということで，一般の惑星を調べる方法についての質問ですけど． (月と地球と太陽しか興味がないのかな?)