３次元上の座標について

イチさんの書込 (2006/07/11(Tue) 13:55)

初めまして，日々土木設計業務を行っているイチという物です．３次元上の座標の出し方について，お聞きしたいことがあります．先日，知り合いの業者から次の質問をいただきました，３次元上の３角形で，その三角形上のｘ・ｙ座標がわかるとき，ｚ座標を求める方法がわかりませんｘとｙがわかっているから最初は簡単だと思っていたのですが，どういう公式を使って，考えればいいのかさっぱりわかりません．よく考えたら３次元の３角形すらどう出したらいいのかわかりませんでした．ぶしつけな質問ですが，お答えいただけると幸いです．よろしくお願いします．．．

Re: ３次元上の座標について

いちさんのレス (2006/07/11(Tue) 15:04)

ひらがないちです．

これは，空間の平面上に三角形を描いて，その座標を求めるということですか？であれば，とりあえず，三角形の面を平面の方程式で表して，x,yを代入すれば求まると思いますよ．高校数学の空間ベクトルがちょうど良いかもしれませんね．

Re: ３次元上の座標について

イチさんのレス (2006/07/11(Tue) 16:31)

早速のレスありがとうございます，平面の方程式ですね自宅に帰って，高校の教科書をあさってみます．

Re: ３次元上の座標について

toorisugari no Hiro さんのレス (2006/07/11(Tue) 17:13)

> ３次元上の３角形で，その三角形上のｘ・ｙ座標がわかるとき，ｚ座標を求める方法がわかりません

これだけでは，条件が不十分です．

「x,y平面上に適当な三角形をおき，これを底面とするz方向にのびる三角柱を任意の角度で切り取った断面」が題意の三角形ですが，このz座標は当然わかりません．

なにか他の条件はありませんか?

それとも三角形を含む平面がすでにわかっていて，x,y座標にたいするz座標を求める問題ですか?

Re: ３次元上の座標について

toorisugari no Hiro さんのレス (2006/07/11(Tue) 18:33)

とりあえず，問題が「空間に三点

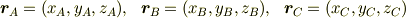
$\bm{r}_A = (x_A, y_A, z_A),~~\bm{r}_B = (x_B, y_B, z_B),~~\bm{r}_C = (x_C, y_C, z_C)$

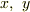がある．これを含む平面上の点 $\bm{r}$ の x,~y 座標がわかっているとき座標を求めよ．」であると決めうちして，解説します．

3点 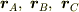$\bm{r}_A,~\bm{r}_B,~\bm{r}_C$ とそれを含む平面上の任意の点 $\bm{r}$ がなす4面体の体積は常にだから，スカラー三重積の考え方より，

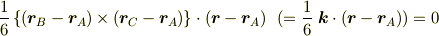
$\frac{1}{6}\left\{(\bm{r}_B-\bm{r}_A)\times(\bm{r}_C-\bm{r}_A)\right\}\cdot(\bm{r}-\bm{r}_A)~~(=\frac{1}{6}~\bm{k}\cdot(\bm{r}-\bm{r}_A))=0$

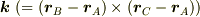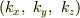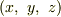となる．定数ベクトル $\bm{k}~(=(\bm{r}_B-\bm{r}_A)\times(\bm{r}_C-\bm{r}_A))$ の各成分を (k_x,~k_y,~k_z) ，平面上の点 $\bm{r}$ の各成分を (x,~y,~z) とすると，上を書き直した式

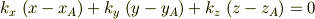
k_x~(x-x_A) + k_y~(y-y_A) + k_z~(z-z_A) = 0

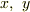は平面の方程式になる．よって，平面上の点 $\bm{r}$ の x,~y 座標がわかっているとき座標は，

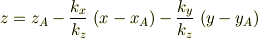
$z = z_A -\frac{k_x}{k_z}~(x-x_A) - \frac{k_y}{k_z}~(y-y_A)$

で与えられる．ただし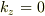， k_z=0 のときは不定である．

Re: ３次元上の座標について

イチさんのレス (2006/07/12(Wed) 15:12)

レスが遅れまして，申し訳ありません，確かに問題としては不十分でした．補足致しますと３次元空間上の三角面の各頂点での座標，ｘ，ｙ，ｚについてはわかっていますその三角面上に有るｘ＝＃＃，ｙ＝＃＃の時のｚ座標を求めなさい．早速，連絡してみます．いちさん，toorisugari no Hiroさん，不慣れな質問にレスをありがとうございました．

[home] [掲示板] [ページの先頭]