POTYOMUKIN さんの書込 (2006/07/09(Sun) 20:23)

質量ｍの質点が，原点からの距離に比例した引力（比例定数ｋ）を受けて，ｘｙ平面上で運動している．運動方程式を解き任意の時刻における質点の座標を求めなさい． また時刻ｔ＝0で質点の座標が（ｘ0，ｙ0），速度がベクトル０であったとして，力学的エネルギーを求めなさい．という問題で， 答えは ベクトルｒ＝（ｘ，ｙ）とおくと，A,B，α，βを任意定数として， ｘ＝Asin((k/m)^(1/2)t+α) ｙ＝Bcos((k/m)^(1/2)t+β) E＝（1/2）ｋ（ｘ0＾2+ｙ0＾2）です．

自分が解いたのは， ベクトルｒ＝（ｘ，ｙ）とおくと ｘの運動方程式 ｍｄ＾2ｘ/ｄｔ＾2＝−ｋｘ この微分方程式を解き， x=Ccos ((k/m)^(1/2)t) C’sin ((k/m)^(1/2)t) となってしまいます． ｘがサインだけの式になりませんし三角関数のなかに+αがでません．ｙも同様で． どうしてなのでしょうか？間違っていますか？

ついでにEは E＝（1/2）mv^2+Uから 速度がベクトル０より（1/2）mv^2は0， U=−∫Fｄｒ ｘは0からｘ0の積分でｙは0からｙ0の積分 E＝（1/2）ｋ（ｘ0＾2+ｙ0＾2）とでました． なので上の式でｍｄ＾2ｘ/ｄｔ＾2＝−ｋｘと力は−ｋｘとおくのは間違ってないかなとおもっているのですが…． どなたか教えてください．お願いします．

yama さんのレス (2006/07/09(Sun) 22:19)

x=Ccos ((k/m)^(1/2)t) C’sin ((k/m)^(1/2)t) は x=Ccos ((k/m)^(1/2)t)+C’sin ((k/m)^(1/2)t) の間違いだと思います． これは定数 A，α を適当に選べば ｘ＝Asin((k/m)^(1/2)t+α) の形に表すことができるということを，高校の数学で学んだと思いますが・・・． これについては，このサイトにも記事があります．

• http://www12.plala.or.jp/ksp/mathInPhys/trifuncCombine/

なんとなく さんのレス (2006/07/09(Sun) 22:59)

POTYOMUKINさん，yamaさん，こんにちは．

なんとなくです．

表記ミスはあるものの，POTYOMUKINさんの解答で合っていると思います． ただ，気になるのが，「答え」の方です． この問題は本質的に２階微分方程式に帰着し，任意定数は２つでいい筈です． 言い換えると，Ａ，Ｂ，α，βの間に関係式が成り立つ筈と思うのですが，そ のことに一切言及されていません． 本当に４つも任意定数があるものでしょうか． なにか・・・不自然な気がするのですが，私の方が間違っているのでしょうか． もし，何か理由があるなら，教えて下さい．

篠原 さんのレス (2006/07/09(Sun) 23:05)

みなさん，こんにちは． 横から失礼します．

なんとなくさん：

x方向，y方向，それぞれについて全く独立に2階微分方程式が作れるので， それぞれの微分方程式に対して，2つの任意定数を持つ解が得られるので， 任意定数は4つでよいのではないでしょうか？

yama さんのレス (2006/07/09(Sun) 23:45)

篠原さんの言われる通り，任意定数は４つでいいと思います． 初めの（x,y）座標と，初速度のx,y成分を任意の値に設定できるからです．

解については，質点の座標を求めるだけなら x=Ccos ((k/m)^(1/2)t)+C’sin ((k/m)^(1/2)t) でもいいのですが，運動の様子を調べるためには，ｘ＝Asin((k/m)^(1/2)t+α) の形にしたほうが見通しがよくなると思います． ｙ＝Bcos((k/m)^(1/2)t+β) とあわせて考えると，互いに直角な方向の２つの単振動を合成したものになるので，軌道は一般にリサージュの図形になることが分かるでしょう． 特に両方向の振動数が等しいので簡単な図形になります． もしα=β ならば，座標軸方向の主軸をもつ楕円になることは容易に分かると思います．そうでない場合も，いろいろな方向の主軸をもつ楕円（特別な場合は円や直線）になることを示すことができます．

CO さんのレス (2006/07/10(Mon) 13:18)

リサージュ図形についてはかぎしっぽ内にも記事を用意しています． 参考になれば幸いです．

• http://www12.plala.or.jp/ksp/mathInPhys/lissajous/

mNeji さんのレス (2006/07/10(Mon) 14:53)

計算を簡単にするために，z=x+iy の複素平面での計算をしてみました．

mNjB:dynamics/xy-pendulum

• http://www.as-ia.co.jp/ykwk/wiki.cgi?dynamics%2fxy%2dpendulum

遡れば，x,yのばね定数が違わない限り，最初の位置を軸とした1次元単振動をしているだけと考えて良いのではありませんか？

ｙama さんのレス (2006/07/10(Mon) 15:31)

初速度が0だったら，その通りですね． しかしこの問題では，初速度が0というのは2番目の設問でエネルギーを求める場合の初期条件であって，その前の「任意の時刻の座標を求めなさい」という設問にはこの初期条件は適用されないように思われますが・・・．

mNeji さんのレス (2006/07/10(Mon) 16:26)

ｙamaさん：

>「任意の時刻の座標を求めなさい」

というのは，一般解が求まっていれば言い訳ですよね．初期条件の付与の仕方は，色々あるので，わざと定数a,bと於いてあるので好きに決めれば良いのでは無いでしょうか？

問題には，初期条件の付け方は明示していませんよね？たとえば，t=0とt=3の位置を与える事もありますよね．

POTYOMUKIN さんのレス (2006/07/10(Mon) 16:45)

みなさん返信ありがとうございます．

リサージュ図形についてはじっくり考えてみたいと思います．

たしかにx=Ccos ((k/m)^(1/2)t) C’sin ((k/m)^(1/2)t)のところで+が抜けていました．すみません． x=Ccos ((k/m)^(1/2)t)+C’sin ((k/m)^(1/2)t)から合成を使って， ｘ＝Asin((k/m)^(1/2)t+α)となるのは分かりました．

しかし ｙの運動方程式 ｍｄ＾2ｙ/ｄｔ＾2＝−ｋｙ この微分方程式を解き， ｙ=Ccos ((k/m)^(1/2)t)+ C’sin ((k/m)^(1/2)t) ｙ＝Asin((k/m)^(1/2)t+α) ここから ｙ＝Asin((k/m)^(1/2)t+α+π-π) ｙ＝-Acos((k/m)^(1/2)t+α-π) ｙ＝Bcos((k/m)^(1/2)t+β) と考えていいのでしょうか？

mNeji さんのレス (2006/07/10(Mon) 17:19)

POTYOMUKIN：

ひょっとして三角関数による微分方程式の一般解の作り方が疑問と言うことでしょうか？

物理に良く出てくる微分方程式は，線形(非微分関数が一次，このばあい，xやy)で，時間に付いての微分が高々2階で，今の場合強制外力がない＝同次，さい次というものです．

これの性質を正確に説明するのには時間が掛かります．次のサイトで勉強することをお勧めします．

線形常微分方程式

• http://www.geocities.jp/ruy406/math/math8.pdf#search=

もとに戻ると，

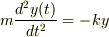
ここ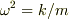で として 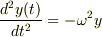の一般解は，

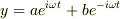と書こうが，

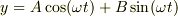と書こうが，

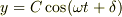と書こうが，

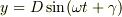と書こうが，

その時に，使いやすい表現を使うだけの事だとおもいます．重要なのは，いずれの場合にも，積分定数として，2個のパラメータを含んでいることです．もちろんこれらの関数は，数学的に等価なので，其々のパラメータは相互に関係を出すことは出来ますよね．

私の場合，三角関数の計算を間違い易いので，なるべく指数表示の式をつかい，最後の方で三角関数に戻すようにしています．

追伸：

全ての式で「k/m」を生のままで使われていますが，簡単な変数wとか，を定義してお使いになったほうが，式も見やすいですし，書きやすくないですか．

特に，試験では，検算する時間が欲しいので，「簡単な変数」は大切ですし，ディメンションチェックもやり易い： を見ると，反射的に，角速度を連想しますから．

ｙama さんのレス (2006/07/10(Mon) 17:39)

POTYOMUKINさんへ

y の場合の積分定数は，x の場合とは異なります．従ってたとえば ｙ=Dcos ((k/m)^(1/2)t)+ D’sin ((k/m)^(1/2)t) のように表して考えてみてください．

ｍNejiさんへ

最初の設問は当然一般解を求めよということだと思います． この場合一般解は４つの任意定数を含み，その定数値を変えることによって任意の初期条件または境界条件に対応する解が得られるものでないといけません． ｘ＝Asin((k/m)^(1/2)t+α) ｙ＝Bcos((k/m)^(1/2)t+β) はこの条件を満たしているので一般解といえます．たとえば，t=0とt=3の位置を与えることによって定数A,B,α,βの値を決めることができます．

しかし初速度を0とした解は，あくまでも特殊解であって任意の初期条件に対応させることはできません． もちろん物理的に同じ運動であっても，時間の原点をずらしたり，座標軸の向きを変えたりすることによって解の形は変わります．その意味では定数のとりかたにはある程度の任意性があります． しかしこの問題の運動では，このような任意性を利用しても初速度を0とすることは一般にはできません．（初速度のx成分とy成分のどちらかを0にすることはできますが） たとえば初期条件を，t=0 のとき，x=x_0，ｙ＝0，v_x=0，v_y=v_0 として任意定数の値を定めると，楕円運動になることがわかります．これは時間の原点や座標軸の向きをどのようにとっても直線運動にはなりません．

mNeji さんのレス (2006/07/10(Mon) 18:04)

ｙamaさん：

>この場合一般解は４つの任意定数

これはそうだと思います．私の式に，定数がa,bだけですが，これは複素数だからです．その意味では1つの複素数は，実部と虚部の2つパラメータを持つので，計4個の初期条件がいります．

>ｘ＝Asin((k/m)^(1/2)t+α) >ｙ＝Bcos((k/m)^(1/2)t+β)

のように，位相表示をお使いの様ですが，計算違いをしやすいので，余弦・正弦を平等に使い方を好みます．さらに途中では，オイラー表現を使うようにしています．これならめったに計算違いしませんから．

特に，試験のように時間が迫ったときに三角関数の検算は，絶対と言って良いほど間違えました，私は...．

yama さんのレス (2006/07/10(Mon) 18:57)

私が言いたいのは 「一般解は楕円運動（その特別な場合として円運動や直線運動も含む）になる．」 ということであって，１次元単振動ではないということです． １次元単振動になるのは，あくまでも特別な場合でなって，一般にはそうはならないということです．

途中の計算には複素数を用いたほうがいいというのには賛成です．

なんとなく さんのレス (2006/07/10(Mon) 22:57)

みなさん，こんにちは．

この問題の微分方程式（系）が４つの任意定数を含む一般解を持ち(mNejiさんのように複素数やベクトルで表現すれば当然２つですが），それが線形空間の固有ベクトル数に一致していることは知っていましたが，何が違和感なのか分かりませんでした． この問題の元々の表現では，原点からの距離に比例する力が働いている系であることでした．もし，これ以外の力が働いていないなら，解は単振動のはずです．実際，極座標で解いてみると，運動方程式は天体の引力(r^-2)を(r)に置き換えたものですから，角運動量保存則とｒ方向の単振動（任意定数２つ）が得られます． この運動で円（楕円）解を得るには，角運動量を与えるため，動径方向以外の初速を与える必要があり，それは，中心力以外の力が原初に働いていることになります．yamaさんの示された例で，ｙ方向速度を与えているのはまさにその例ですね． つまり，問題に忠実に考えれば，初期条件の選び方にはおのずと制限があり，この解答は拡大解釈であるように見えたということです． まるで宇宙開闢時の神の一撃のような話ですが，一般論としては兎も角，問題の意図としてはどうなのでしょう．私的には疑問は払拭しましたが・・・．

mNeji さんのレス (2006/07/10(Mon) 23:49)

yamaさん：

話が入り組んできたので，私の計算でも，初期条件として，t=0の時の位置，速度を与えた場合の一般解を「応用問題(II)」として示しました．一応，余弦・正弦で表示してありますが，この方が初期条件の寄与の仕方が明確で，検算も楽だとおもいます．

なんとなくさん：

>問題に忠実に考えれば，初期条件の選び方にはおのずと制限があり，この解答は拡大解釈であるように見えたということです．

というような難しい状況ではなく，単に運動の自由度が2(xy or rθ)のどちらを選択するかどうかです．バネの力は，保存力ですから，当然，天体と類似の振る舞いをします．各運動量は保持します．

>中心力以外の力が原初に働いていることになります．

それを初期条件として取り込んでいるのではありませんか？ 通常の1次元のバネだって，平衡の位置からズラシテ，手を離す，その瞬間には手が重りに力を与えていますね．

あまり難しい解釈は必要ないとおもいます．むしろ微分方程式を確り解いて，初期条件を決める方法を，シンプルな計算で実行するべきと思います．

yama さんのレス (2006/07/10(Mon) 23:54)

なんとなくさんへ

初期条件を与えるために，はじめにだけ他の力がはたらくと考えるのはごく普通のことだと思います． たとえば，重力による運動を考える場合，ある方向にある速さで投げ出された物体の運動を考えるのは普通だと思います． もし，重力以外の力が初期条件としてもはたらくことを認めないなら，重力による運動は自由落下だけになってしまい，いわゆる放物運動は除外されてしまいます． また，ケプラー問題でも，惑星はまっすぐ太陽に落ち込むことになります．楕円運動をさせるためには神の一撃が必要になります．

このように考えると，初速度0の場合しか考えないというのでは，運動方程式の適用範囲を著しく狭めてしまうように思われます．

yama さんのレス (2006/07/11(Tue) 00:21)

mNejiさんへ

確かに応用問題(?)では初期条件との対応が明確になっていますね． その反面，軌道の形がすぐにはわかりにくくなりましたが，これはやむをえないところでしょうね．

なんとなく さんのレス (2006/07/11(Tue) 00:42)

mNejiさん，レス有難うございます．

難しく考えてるわけではなくて，作問のマナーとして，曖昧さの排除が為されていないのではないかということです． mNejiさんの例でいえば，おもりを垂直に持ち上げたり引っ張ったりしても，単振動ですが，横に振れば２次元でバネ振り子の扇形を描きますよね．この二つは別の問題です．これを単振動の初期条件で解く人はいないでしょう． 私は回答者でなく，問題を出す側の意図に疑問を感じているのです．

>yamaさん 将に今の放物問題は，きちんと初速ベクトルをあたえるという一文があります．この問題の特異性はその様な条件明記が無い分，裏返せばなんでもありです． それと，初速度は必ずしも「０」である必要はありません．ｒ方向（ｒ逆方向）を向いていればいいわけです． 或いは深読みすれば，初期条件によって軌道（の性質）が大きく変わること，その条件が運動にどのような変質をもたらしているのか，学ぶ問題かもしれません．

ただ，これらの考察は前も書いたとおり，一般論としてはいいが，問題はもっと明らかなシチュエーションを示すべきだと思っているまでです． 私なら，重力の問題を例にあげれば，物理的に正確ではないですが， 「空間に質量ｍの物体が速度ｖ（０もあり得る）で等速運動している．この物体が或る中心から距離のみに比例した力を受け始めたとき，その後の無体ｍの運動を論ぜよ」 かな．

yama さんのレス (2006/07/11(Tue) 01:37)

最初の設問では，初期条件は何も指定されていません．初期条件が指定されていない以上，どんな初期条件にも対応できるような一般解を求めるのが自然だと思います．また，初期条件を意識せずに運動方程式を解いていけば，自然に一般解が得られます． 従って任意定数を含む一般解を求めよということだと私は解釈しました． 動径方向の運動だけに限定されると解釈するのは無理があるように思います．

この問題は単なる１次元単振動の問題ではなく，いわゆる空間振動子(３次元振動子)の問題だと思います．つまり，３次元空間で中心からの距離に比例する引力がはたらく物体の運動を考えるわけです． この場合の運動は一般に，ある平面上の楕円運動になります．この問題では，はじめからその平面上に限定して考えているのだと思います． 万有引力による運動でも，有界な運動は平面上の楕円運動になりますが，有界な運動が閉じた曲線になるような中心力は，距離に比例する引力と万有引力のような距離の-2乗に比例する引力だけであることが分かっています． また，中心力なので万有引力と同様に角運動量が保存します． さらに２方向の単振動の合成と考えることもできます． この運動はこのようにいろいろ興味深い特徴をもっていますが，１次元単振動になるような特別な場合だけに限定したのでは，この運動の一般的特徴をほとんど無視することになってしまいます．それはないだろう・・・と思うのですが．

なんとなく さんのレス (2006/07/11(Tue) 08:50)

>yamaさん，こんにちは．

たびたびレスを頂き，有難うございます．多分，私の意図したいことが伝わっていないと思うのですが，この問題は基本的にyamaさんの仰るとおりの内容を含んでいます．中心力場による運動はお指摘のような特徴があることも勿論，よく存じています．

つまり，そのような豊富な，いわば突付きまわさねばならない命題を，安易にｘ，ｙ方向の決まりきった解法で理解した，としていいのかどうか，ということです． なるほど，答えは一般解であり，その初期条件ですべての解を構成できることはそのとおりです．しかし，これまで議論したように，初期条件と軌跡の深い関わり， 中心力場の特徴など，を感得させる出題であるのか，という疑問です．

端的に言えば，微分方程式の練習問題か？と思えます．2番目の問題の難易度とのバランスもそう示しているように思います．

戯言を言えば，専門が「物理」で出された出題の「匂い」がしない，気がするのです．このニュアンス，分かって頂けるでしょうか．

ｙama さんのレス (2006/07/11(Tue) 12:55)

設問が２つだけで終わりなのか，他にもあるのか，あるいは今回はこれだけで，別の機会に関連した内容を扱うのか，そのあたりの事情がよくわからないのですが，設問２つで終わってあとは何もないというのだったら，なんとなくさんのおっしゃる通り，単なる微分方程式の練習問題という意味しかないでしょうね． ただ練習問題だとしても，出題者はこの運動の特徴がわかっているはずなので，１次元の単振動の問題として出題したのではなく，あくまでも２次元の問題として一般解を求めさせようと意図したのだと思います.

なんとなく さんのレス (2006/07/11(Tue) 13:32)

>yamaさん．

あれこれ，すみません．

本当の問題の設定がどの程度か，どういう経緯で出題されたのか分からない以上，あまり意味はないのですが，付き合って頂いて，得心しました． 問題を解くための問題ではなく，「物理」を考える問題が必要ではないかと思う今日この頃です． また，よろしくお願いします．

ｙama さんのレス (2006/07/11(Tue) 17:13)

こちらこそよろしくお願いします． いろいろご意見いただきありがとうございました．

POTYOMUKIN さんのレス (2006/07/12(Wed) 19:01)

多くの返信ありがとうございます． じっくり理解していこうと思います． 本当にありがとうございました．