遅延時間とコンデンサ容量について.
遅延時間とコンデンサ容量について.
ゆうこ さんの書込 (2006/07/08(Sat) 11:24)
コンデンサ容量が1fFと10fFのときの遅延時間をシミュレーションしました.R=T/Cより,10fFを1fFと1/10にしたら遅延時間も1/10になると思ったのですがならなかったのはなぜですか??
Re: 遅延時間とコンデンサ容量について.
mNeji さんのレス (2006/07/08(Sat) 11:35)
はじめまして.
ゆうこさんに幾つか教えて欲しいことがあります;
1)学校と学年は? 2)どんな回路をつくって, 3)どんな計器をつかって,何をそくていしましたか?
2),3)は絵にかけなくても,言葉で,慌てずに説明してくださいね.
Re: 遅延時間とコンデンサ容量について.
ゆうこ さんのレス (2006/07/08(Sat) 13:07)
すみません,慌ててたもので何も説明できてなかったですね.
大学3年です.
使用したものはインバータ回路です.
┬vdd 5.0V │ │ │┌┘ ┌〇││ ││└┐ │ │ in――┤ ├───┬─out │ │ │ │ │┌┘= コンデンサ └─┤││
│└┐|
│| │| ┴┴ /// ///
0Vと5Vの間で変化する電圧を加えたときにoutから1/0反転に反応する電圧が出力されました.2.5Vの所で1/0変化したということにしました. この回路でコンデンサ容量を様々なものに変化させて遅延時間を計りました. 遅延時間は回路シミュレーションをして入力0→1出力1→0のときと入力1→0出力0→1の2種類をそれぞれのコンデンサ容量のときに測りました.
結果は以下の通りでした.
コンデンサ 入力0→1 入力1→0 容量 出力1→0 出力0→1 (fF)tpd(ps) tpd(ps) 1 65.1595 60.7266 2 66.8237 62.9144 5 71.9851 68.2666 7 76.0322 70.414 10 79.9019 76.4357 12 83.7064 78.0938 15 88.2871 82.2482 17 91.3794 85.2119 20 95.3636 91.0554 50 135.683 129.217 70 164.424 153.75 100 207.424 193.816
何か足りないようでしたらまたお願いします.
Re: 遅延時間とコンデンサ容量について.
ゆうこ さんのレス (2006/07/08(Sat) 13:11)
上のがずれてしまったので書き直します. パスっも入れ忘れちゃったのですみません...
┬vdd 5.0V │
││┌┘ ┌〇││ pmos
|│└┐ ││ in―┤ ├───┬─out
│ │ │
│ │┌┘= コンデンサ └─┤│nmos│ │└┐| || │| ┴┴ /// ///
Re: 遅延時間とコンデンサ容量について.
mNeji さんのレス (2006/07/08(Sat) 13:44)
エレクトロニクス(半導体)は苦手な世代(老人ともいう)です.感触では,Cに充電した電気量がnmosの比較的に高いインピーダンス成分により放電していく時に,充電電位の1/2になるまでの時間を計測することでCを出すようにしているのでしょうか?
この場合,時定数を決めるRが,nmosに左右されるので,むしろもっと大型の容量(uF)とある程度確実な抵抗(Mohm以下)にして,直接電位の時間変化をオシロスコープで観察する方が善い様にもおもいます.
せめて,時間領域の測定としても,psのオーダは短すぎるようにも思います.
CにRが並列の場合の,電位の時間化はexp(-t/τ)になりますよね.
Re: 遅延時間とコンデンサ容量について.
mNeji さんのレス (2006/07/08(Sat) 14:08)
どうもオオボケしていたかもしれません.
例えば,放電のときに単位1の電圧で,単位0.5の電圧の時の時間tを考えると;
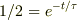
従って,自然対数を取れば
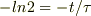
整理して
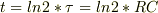
という意味では,tはCに比例しますね.
ところが,お示しのデータをプロットすると,C=0のところで,有意な値を示しています.nmosの浮遊容量は如何程でしょうか? ないしは,配線等?
Re: 遅延時間とコンデンサ容量について.
mNeji さんのレス (2006/07/08(Sat) 14:28)
浮遊容量と仮定すると,約40fFに見えますね.
確認の為に,コンデンサを外して測定してみると良いですね.それがもっともらしければ,今後の測定の時に,堂々と「浮遊容量を補正済み」と言えます.
Re: 遅延時間とコンデンサ容量について.
篠原 さんのレス (2006/07/08(Sat) 15:19)
ゆうこさん,はじめまして. mNejiさん,こんにちは. 篠原です. 横から失礼します
まず初めに.... ゆうこさん,以下の掲示板でも全く同じ質問をされていますね.
マルチポストは当掲示板の利用規約にて禁じられています. 回答者に対して,失礼だとは思いませんか?
つい先日,私も同様の計算をしました. シミュレーションじゃなくて,紙面上で,ですけど.
確かに,遅延時間は負荷容量に比例するはずです. でも計算結果を見る限り,単調増加ではありますが,比例関係にはなっていないようですね. mNejiさんの仰るように,浮遊容量が聞いているのでしょうか・・・ 浮遊容量が聞いているのなら,それに対してもっと大きな容量のコンデンサをつなぐことによって確かめることは出来ますよね.
また,問題の設定がまだ良くわかりません. シミュレーションを行ったのなら,それに用いたMOSFETのパラメータがあるはずです. それらの中に,浮遊容量,その他の遅延時間に関係しそうなパラメータはありませんか? シミュレーションに使ったパラメータ示してください.
Re: 遅延時間とコンデンサ容量について.
なんとなく さんのレス (2006/07/08(Sat) 16:15)
みなさん,こんにちは.
私も少し疑問があるので,勝手ながら参加させてください.
時定数τ=CRは,相対強度が1/eになる時間ではなかったかと思うのですが,あまり今の問題に関係ないですね.
それにしても,容量がfF(フェムトファラッドでしょうか),おそろしく小さいですね.時定数もps(ピコセカンド)でしょうか,これまた小さい.どうやって計測しているのでしょう?オシロスコープでもナノセカンド以下がそんなに簡単に計測できるものなのですか?ちょっとびっくり.
それはともかく,単純に考えれば,たとえば出力Highでは,p-MOSのみがアクティブになり,電源電圧が測定コンデンサの両端に現れるものだと思います. このとき,p-MOSの(内部)浮遊料量C',抵抗Rとすれば,C,C',Rが直列なので, 時定数は,τ=(C+C')R となります.計測値はこれを与えるので,取付けの測定コンデンサCを評価するためには,差分をとる必要がありますよね. つまり,τ'-τ=CR(C',Rは変化しないから) として,データを見直せば,コンデンサの容量差が2倍になれば,時定数(差)もほぼ2倍となり,ほぼ直線状に並んでいるのが見て取れます.最小二乗法で評価すれば,内部抵抗値は1.4KΩ程度となりました.MOSの動通時,抵抗値ですから,そんなものかな,という気がします.ちなみに非動通時は数MΩですから,矛盾はないと思いますが,このような単純な考えではだめなのでしょうか. いまいち,分かりませんが,実験データとしては整合してる気がします.
Re: 遅延時間とコンデンサ容量について.
篠原 さんのレス (2006/07/08(Sat) 16:36)
なんとなくさん,こんにちは.
なるほど. 実験データはいじってみていないので, なんともいえませんが,浮遊容量ということで,つじつまあが合うのですね? メデタシ,メデタシ(?)
ちなみに,遅延時間を実際に測定するのは,ごく簡単です. 多数の奇数個(例えば101個)のインバータを直列に接続して,ループを作り,その発振周期を測定すれば,すぐに出ます. そこから,理想的なMOSを仮定すると,容量も計算することも出来ます.
また,MOSFETの導通時のオン抵抗ですが,1.4KΩでは大きすぎると思います. 今の場合,MOSFETの過渡的な現象が関連しているます. (FETがオフ領域→三極管領域→飽和領域と変化するため) そのため,純粋な抵抗で近似すると,実際のオン抵抗よりもかなり大きな値になってしまうのでしょう・・・. (計算する上で,このような内部抵抗を仮定することは,有効だと思います.)
Re: 遅延時間とコンデンサ容量について.
なんとなく さんのレス (2006/07/08(Sat) 16:56)
>篠原さん.
なるほどー.そうか,沢山繋げればいいのか.確かにMOSの抵抗が大きすぎるなとは思ったのですが,詳しいですね. 実験の話は現実的な効果や特性などからんで,数量的な評価は難しいですね.理論が簡単とは言わないけれど・・・(^o^;). 勉強になりました.ありがとうございます.
Re: 遅延時間とコンデンサ容量について.
かつ さんのレス (2006/07/08(Sat) 21:16)
横から失礼. 篠原さん: > FETがオフ領域→三極管領域→飽和領域と変化するため 三極管領域では無く,五極管特性領域ですね.三極管は電圧性,五極管は 電流性です.
それは兎も角,これって,どこの時間を計っているのか良く分からないの ですが・・・もし入力 ON/OFF -> 出力 OFF/ON の時間なら,自分の入力 容量と測定系の出力抵抗分/インダクタンス分/浮遊容量で作られる遅延の 方が大きかったりして? (^^;
Re: 遅延時間とコンデンサ容量について.
篠原 さんのレス (2006/07/08(Sat) 21:55)
かつさん,はじめまして. 篠原です.
> > FETがオフ領域→三極管領域→飽和領域と変化するため > 三極管領域では無く,五極管特性領域ですね.三極管は電圧性,五極管は > 電流性です.
すみません.
順番を間違えた事を認めます.
オフ領域→飽和領域→三極管領域
の間違いです.
しかし,この領域を五極管領域というのは,私は存じ上げておりません.
私の知る三極管領域では,直線領域ともいい, 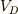 に対して,
に対して, 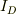 が増加する領域を指します.
(2次関数となる.)
この領域は,ゲート電圧
が増加する領域を指します.
(2次関数となる.)
この領域は,ゲート電圧 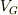 が,しきい値電圧
が,しきい値電圧 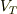 よりも大きく(
よりも大きく( 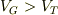 ),ゲート-ドレイン間の電圧が
),ゲート-ドレイン間の電圧が 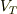 よりも大きい領域を指します
よりも大きい領域を指します 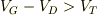 .
(このときのドレイン電流はドレイン飽和電流
.
(このときのドレイン電流はドレイン飽和電流 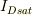 よりも小さくなります.)
この領域では,真空管の三極管特性と同様,ドレイン電圧と共にドレイン電流が増加するため,三極管領域,もしくは直線領域(実際には直線ではありませんが,直線で近似するんですかね?)と認識しております.
よりも小さくなります.)
この領域では,真空管の三極管特性と同様,ドレイン電圧と共にドレイン電流が増加するため,三極管領域,もしくは直線領域(実際には直線ではありませんが,直線で近似するんですかね?)と認識しております.
まだまだ勉強中なもので,半導体を専門としているにもかかわらず,FETにおいての五極管領域というものをまだ聞いたことがありません. 飽和領域のことを五極管領域というのでしょうか?? もしよろしければ,教えていただけるとありがたいです.
かつさん,よろしくお願いいたします.
追加:
調べました. どうやら飽和領域のことを,五極管領域とも言うのですね. 一つ勉強になりました. ありがとうございます.
Re: 遅延時間とコンデンサ容量について.
かつ さんのレス (2006/07/09(Sun) 10:48)
篠原さん: これはどうも,こちらこそ失礼しました. 線形領域を三極管領域と呼ぶ,というのを知らなかったもので.
昔は普通の半導体の特性を五極管特性,SITのそれを三極管特性,なんて 言ってました.爺の戯言です(w 何しろ,私の頃は教科書に真空管が載ってたりしたわけでして A(;^^)
Re: 遅延時間とコンデンサ容量について.
篠原 さんのレス (2006/07/09(Sun) 11:29)
かつさん:
線形領域という言い方が最も一般的なようですね. (ネットで調べてみると・・・) なるほど.
三極管特性,五極管特性という言葉は今でも使いますよ. 電流電圧特性が飽和する半導体を五極管特性といい,飽和しない半導体を三極管特性といっています.
残念ながら私は真空管の理論や特性を学んだことも,実際に設計をしたこともないので,実際の三極管,五極管がどのようなものなのか良くわからないのではありますが・・・
とっても良い復習になりました! ありがとうございます :)