代数学(物理で関係ないはずなのにでてきました)
代数学(物理で関係ないはずなのにでてきました)
広 さんの書込 (2006/07/07(Fri) 21:01)
先生が代数学が好きなもので次の問題を考えてきて欲しいとおっしゃったのですが・・・
pを素数として,Q(√p)={a+b√p|a,b∈Q}とおく.Q(√p)は体で,Q 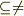 Q(√p)
Q(√p) 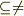 Rdearu.
いまqをpと異なる素数とするとき,√q
Rdearu.
いまqをpと異なる素数とするとき,√q 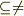 Q(√p)を示し,さらにこれからQ(p)
Q(√p)を示し,さらにこれからQ(p) 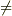 Q(q)であることを示せ.
Q(q)であることを示せ.
ヒントやご意見なんでも参考になりますのでよろしくお願いします.
ちなみに 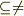 は含まれないの意味の記号をどのようにすればいいのかわからなかったのでそのように表現しました.もしそれを知っている方がいれば教えて欲しいです.
は含まれないの意味の記号をどのようにすればいいのかわからなかったのでそのように表現しました.もしそれを知っている方がいれば教えて欲しいです.
Re: 代数学(物理で関係ないはずなのにでてきました)
Chappy さんのレス (2006/07/07(Fri) 21:44)
はじめまして,Chappyというものです.
まず 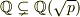 は定義通りですが,
Rdearuってなんですか??僕が知らない記法なのですかね.
とはいっても,僕は代数が専門ではないので,詳しいことは知りませんが...
は定義通りですが,
Rdearuってなんですか??僕が知らない記法なのですかね.
とはいっても,僕は代数が専門ではないので,詳しいことは知りませんが...
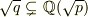 は
正しくは
は
正しくは 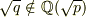 だと思われます.
だと思われます.
証明には背理法がよいのではないかと思います.
ちなみに, 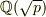 というのは,有理数全体
というのは,有理数全体 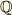 に
に 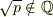 を
付け加えて,集合
を
付け加えて,集合 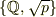 が体になるように
が体になるように 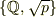 の元を増やしたものです.
これが理解できるとたちどころに問題が分かるのではないでしょうか?
例えば,方程式
の元を増やしたものです.
これが理解できるとたちどころに問題が分かるのではないでしょうか?
例えば,方程式 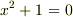 の解は複素数
の解は複素数 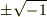 ですが,
ですが,
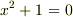 は実数体
は実数体 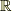 では解をもちませんね?
なぜなら,複素数は実数ではありませんから.
ところが,
では解をもちませんね?
なぜなら,複素数は実数ではありませんから.
ところが, 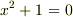 は実数に虚数単位を付け加えたもの,
は実数に虚数単位を付け加えたもの, 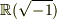 上では解をもちます.
実は,
上では解をもちます.
実は, 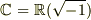 です.考えてみてください...
です.考えてみてください...
”先生”とは高校の先生ですか?そして,あなたは高校生ですか? 僕は高校時代,よく物理の先生と一緒に数学を考えてました,懐かしいです... 大学入った今でも,親交があります. いや,つい思い出にひたってしまってすみません,,,,
Re: 代数学(物理で関係ないはずなのにでてきました)
広 さんのレス (2006/07/07(Fri) 22:01)
Rであるの間違いです.すいません.大学一年です.確かに高校の頃の物理の先生にはお世話になったものです.懐かしい・・・と言っても三ヶ月前のことですが.
Re: 代数学(物理で関係ないはずなのにでてきました)
Chappy さんのレス (2006/07/07(Fri) 22:06)
そうですか,やっぱり高校の先生でしたか..
表記間違いを直すと,最初のところは
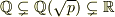 となりますね.
となりますね.
僕の返答に間違いが多くてすみません.. すべて直しておきました.
それと, 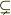 はsubsetneqと書きます..
あとは
はsubsetneqと書きます..
あとは 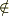 notinなどでしょうか...
notinなどでしょうか...
Re: 代数学(物理で関係ないはずなのにでてきました)
Chappy さんのレス (2006/07/07(Fri) 22:58)
僕の挙げた例を詳しく示してみることとします.
まず, 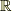 に
に 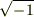 を加えます.
を加えます.
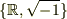 (←あまりよい表記ではなかったです.
正しくは
(←あまりよい表記ではなかったです.
正しくは 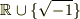 です.
です.
しかし,ただ虚数単位を付け加えただけでは体にはなりません.
まず,乗法について閉じていなければなりません.
したがって,虚数単位の実数倍を含まねばなりません.
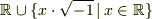 また,
また, 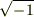 同士の乗法については
同士の乗法については 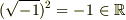 です.
さらに,加法について閉じていなければなりません.
したがって,今まで生成した元の和をとったものも含まなければなりません.
です.
さらに,加法について閉じていなければなりません.
したがって,今まで生成した元の和をとったものも含まなければなりません.
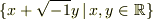 これが求めたかった体です.すなわち,複素数体
これが求めたかった体です.すなわち,複素数体 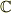 です.
生成の経過をまとめると,
です.
生成の経過をまとめると,
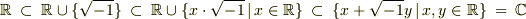
Re: 代数学(物理で関係ないはずなのにでてきました)
Chappy さんのレス (2006/07/07(Fri) 23:29)
大学の物理の先生が,代数の問題を出したんですね! 勘違いしてしまいました.
出題の流れから判断して,最終的に示すことは,
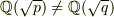 だと思われます.
上の例を参考にがんばってみてください...
だと思われます.
上の例を参考にがんばってみてください...