バネの上端を動かす問題
バネの上端を動かす問題
hajime さんの書込 (2006/07/07(Fri) 01:05)
毎度毎度すいません.次の問題はまったく検討がつきません.
自然の長さb,バネ定数kのバネの下端に質量mのおもりをつるし,上端oを上下に動かし,Asinwtで表される振動をさせるとき,おもりの運動はどうなるか??
ただし,
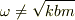
Re: バネの上端を動かす問題
mNeji さんのレス (2006/07/07(Fri) 12:02)
まず静止したエレベータでも考えて,エレベータを吊り下げている点を原点とした静止座標系からした向きに座標値 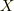 をバネの下端点(動き出す前の静止位置)に取ることにします.このとき,エレベータの天井の座標
をバネの下端点(動き出す前の静止位置)に取ることにします.このとき,エレベータの天井の座標 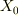 ,エレベータの天井からバネの静止位置までの長さ
,エレベータの天井からバネの静止位置までの長さ 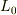 とすると;エレベータが動くと重りも静止位置からずれてます.そこでエレベータに固定された非慣性座標として,重りの静止位置を原点として,下た向きに
とすると;エレベータが動くと重りも静止位置からずれてます.そこでエレベータに固定された非慣性座標として,重りの静止位置を原点として,下た向きに  を取ります.
を取ります.
他方,エレベータに固定されている加速座標系(x)も,エレベータが動きかじめるまで静止している時のバネの下端点を座標原点とします.また,静止系からみたエレベータの天井の座標をx_0とします.
すると,座標については

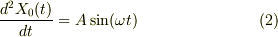
静止座標で考えると,外力は重力だが,端点の位置でバネの伸びとバランスしているので考えなくても良い;
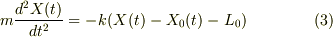
よって, 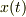 について整理すると
について整理すると
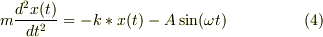
Re: バネの上端を動かす問題
yama さんのレス (2006/07/07(Fri) 14:08)
支点が振動するときのばねの運動なので,普通に慣性系での運動方程式を作ればいいと思います. 支点が動いていないときの釣り合いの位置を原点とした座標をxとすると,支点が動いていないときには,おもりにはたらく力が -kx になることはわかると思います. 支点が振動するときは,つりあいの長さからのばねののびが x-Asinwt になるので,おもりにはたらく力は -k(x-Asinwt)になります. これで運動方程式がつくれますが,強制振動の方程式になりそうですね. もちろん,mNejiさんのように考えても同じことにはなりますが・・・,
Re: バネの上端を動かす問題
hajime さんのレス (2006/07/07(Fri) 20:30)
ありがとうございます.確かにbではなくて/でした.すいません.
Re: バネの上端を動かす問題
mNeji さんのレス (2006/07/07(Fri) 22:17)
yamaさん:
私の経験から,静止(慣性)座標系と加速運動(非慣性)座標系とを誤認する人が多いこと.むしろ,その違いがあやふやで,何が本当の外力で,何が見かけの力かを決めかねる方が多いと思います.
その点, 今回の質問者の hajimeさんは,「加速度を与えられる」というのを,どのように表現するべきか悩んだのだろうと感じました. このような疑問の立て方はとても大切だとおもいます.(問題を解く量よりも,大切だろうと推測します.)
恐らく,似たような問題が自分の実験で出てきたら,非慣性系にあるところから,直ぐに見かけの力を出したと思います.でも,符号などで自信がなくなったら,直ぐに慣性系から再出発するでしょう.
ですから,力学系の計算では,第一番に慣性系(基底ベクトル)を確認して,そこから非慣性系(基底ベクトル)への変換を意識しているのが重要だろうと思っています.
そう思うと,遠心力,コリオリの力も怖くない!,とか.
Re: バネの上端を動かす問題
yama さんのレス (2006/07/07(Fri) 23:51)
慣性系で考える限り,見かけの力を考える必要はありません.はたらく力はすべて本物の力です.従って非慣性系で考えて見かけの力をを持ち込むとかえって混乱して分かりにくくなるのではないか・・・と思ったのですが,人によって受け取りかたは違うでしょうね.まあどちらでも自分にとって理解しやすいやりかたで考えればいいと思います.
Re: バネの上端を動かす問題
なんとなく さんのレス (2006/07/10(Mon) 22:29)
こんにちは,なんとなくです.
>mNejiさん,yamaさん.
どうも,この問題には違和感があったのですが,支点をAsin(ωt)で強制的に動かす場合,支点変位の加速度成分がおもりに掛かるのではないか,と考えていました. つまり,運動方程式は, md^2x/dt^2=-kx+mAω^2sin(ωt) ではないかということです.第二項は支点が静止している座標系では,無論,見かけの力に一致します. 隠し立てするつもりは毛頭ないので,経緯を書いておきますが,私の力学の教科書ではおもりに強制力Asin(ωt)が働くときの強制振動解が出ていて,運動方程式は md^2x/dt^2=-kx-Asin(ωt) なのです.で,変位に対しては上記の式が正しいのではないかと思っていたのですが,物理事典に本問題が出ており,解答は上記の式でした.事典だから正しいとは限りませんが,よろしければ,お考えをお聞かせください.
Re: バネの上端を動かす問題
mNeji さんのレス (2006/07/10(Mon) 23:58)
私の見解は,
>2006/07/07(Fri) 12:02 No.10225 の(4)
の導出に書いた通りで,それ以上でも,それ以下でもありません.
むしろ,どこかで書いたと思いますが,適当に非慣性系で見かけの力を出すと符号が混乱するから,最初に運動方程式を立てるのは,面倒でも慣性系で式を立てるべきだと言っている積りです.
ーーーーこの間,他のことをしていたが...ーーー
今思い出しましたが,(2)にエレベータの天井部の加速度を定義しています.これは座標を下向きに取っていることを前提に書いています.それは,問題に座標の方向が明示されていなかったからです.
(2)をわざわざ書いたのは,この符号でひと悶着すると思っていたからです.普通の問題ならば,加速度を定義するとき,その座標の向きを明示する筈だからです.ただ,そのようなことはマイナーであり,式の作り方を明確にする方が重要と考えたからです.
今後,質問される場合,課題の問題は完全に出すようにしないと,回答者は回答する前に納得するまで逆質問するか,面倒だから回答しなくなるかのどちらかだとおもいます.
ーーーーーーーーーーーーーーーーーー 追伸:
このような場合の訂正的なチェック方法
いま自分が巨人になってエレベータを手で動かせるとします.
仮にエレベータを急加速して上方に動かすとします.式で言えば
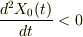
その時,重りがどう動くかと言えば,慣性の法則で,それまでの位置を保持したがるので,バネは伸び,
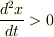
だからエレベータ中に発生する見かけの力は,エレベータ天井に掛かる加速度と符号が逆に見える筈です.
でも,こんなことを試験中に冷静に出来るとは思えません.むしろ静止系で淡々と式をつくり,その後に座標変換をするのが賢いと思います.
私のTipsはこれでお仕舞です.
Re: バネの上端を動かす問題
yama さんのレス (2006/07/11(Tue) 00:42)
慣性系で考える限り,おもりにはたらく力は,ばねの力と重力だけです. 重力は,つりあっているときのばねの長さに関係するだけなので,おもりにはたらく力は,つりあいの長さからのばねののびだけで決まります. つまり,ある瞬間におもりにはたらく力は,その瞬間のばねののびだけで決まり,ばねがのびる速さやのびる加速度には無関係です.ただし,もちろんばね自体の質量は無視できるものとします.
Re: バネの上端を動かす問題
なんとなく さんのレス (2006/07/11(Tue) 13:23)
>yamaさん.
そう言われれば,そんな気もしますが,その機構の物理的説明はどう考えればいいのか,ちょっと混乱しています. 例えば,ばねの代わりに細いピアノ線だとすると,支点(錘の反対側)が加速度運動をすれば,錘も同じ力を受けて加速度が生じますよね.これがコイルだと,なぜ,そうならないのか.コイルの弾性に吸収され,結局伸びしろになるからなのか.あるいは,ばねの上を力が伝わる速度のせいか. 静止系で見れば,コイルの上端は明らかに外部から力を受けているが,それがなぜ錘に伝わらないのか不明です.
Re: バネの上端を動かす問題
yama さんのレス (2006/07/12(Wed) 00:37)
ピアノ線でおもりをを引き上げる場合,ピアノ線に加える力とおもりにはたらく力が等しくなるので,ピアノ線に加えた力がピアノ線を伝わってそのままおもりにはたらくと考えることもできそうに思えます. では,ピアノ線のかわりにばねを用いた場合はどうでしょうか. 話を簡単にするため,無重力状態でおもりにばねをとりつけてばねの端を引っ張る場合を考えます. ばねを力Fで引くとき,おもりにはばねの力 f がはたらき,加速度aが生じたとすると,おもりの運動方程式は ma=f になります.一方,ばねにはおもりからの反作用 -f がはたらきますが,おもりの質量が無視できるならば,この力はおもりを引く力Fと釣り合わないといけないので f=F となり,その結果,運動方程式は ma=F になります.つまりばねの端に加えた力がばねを伝わってそのままおもりにはたらくことになります. 注意しないといけないのは,a はおもりの加速度であって,ばねの端の加速度ではないということです.ばねは伸び縮みするため,ばねの端の加速度 a'はおもりの加速度aには等しくないからです.従ってばねの端を引く力Fは,F=ma であって,F=ma' ではないことになります.
Re: バネの上端を動かす問題
なんとなく さんのレス (2006/07/12(Wed) 01:52)
>yamaさん.
こんばんは.いつも有難うございます. 支点がAsin(ωt)で振動するタイプの問題は,結局バネの長さに繰り込まれた効果として,重りの振動に注目すれば良いようですね.思ったより微妙な問題でした. 解に関しては,yamaさんやmNejiさんと同じ解答を与えている(勿論同じ条件)ものもあります.事典が間違っている公算が大きくなりましたが,さらに調べて相違を明らかにしたいと思います.強制振動解も少し異なるようです. 勿論,このa,a'の差が共振を起こすことは同じですが.
Re: バネの上端を動かす問題
なんとなく さんのレス (2006/07/13(Thu) 10:13)
こんにちは.
いろいろ考えたのですが,結論はやはり運動方程式 md^2x/dt^2=-kx-mAω^2sin(ωt)・・・? が正しいと思います. この方程式は御指摘のとおり「おもり」に対する力のつりあいから得られるものですが,ばねの上端(以下上端と略)の運動はばね自体の伸びに(ばねが質量0として)直接影響しないと考えるのが妥当と思います. 強制力無しに対し,ばねが余分に伸びるのは,あくまでも,あもりに働く力の増加によるものであり,上端の変位は「ばね+おもり」の系全体へ働くものですが,上記理由により,おもりにのみ効果が現れるのだと思います. 通常の教科書では,強制力を変位でなく,「力」そのもので,F=Asin(ωt)のように与えますが,そのときの運動方程式は md^2x/dt^2=-kx+Asin(ωt)・・・? となります.この各項は勿論すべておもりに掛かる力で,矛盾しません. ばねは,自然長をl,ω0=k/m,とすると,変位をxとして,l+g/ω0^2+xとあらわされますが,運動方程式?,?はこのxについて成り立つ式ですよね. つまり,?式の右辺はばねの反作用,および外部(駆動)力を表しています.
ここで,yamaさんもmNejiさんも,
>支点が動いていないときには,おもりにはたらく力が -kx になることはわかると思います.支点が振動するときは,つりあいの長さからのばねののびが x-Asinwt になるので
を出発点にして居られます.しかし,これは自明でしょうか?Asin(ωt)はあくまで,上端の変位です.これに対し,おもりまでの「ばね」はこの変位をそのまま伝えないのではないでしょうか.yamaさんがご指摘のように,上端とおもりの運動は異なります.変位xを未知として,おもりに働く力を純粋に考える必要があります.この,いくら伸びるか不明のxについて,運動方程式は md^2x/dt^2=-kx-mα(α:系加速度) とならねばなりません.これは静止系(慣性系)で見ても,運動系(右辺第二項は見かけの力)で見ても成り立つ式です. したがって,?がやはり,正しい式だと思います.
以上が私の結論ですが,まだ錯誤があるかもしれません.長文失礼しました.
Re: バネの上端を動かす問題
yama さんのレス (2006/07/13(Thu) 12:35)
?式を変形すると次のようになります. d^2x/dt^2=-((ω0)^2)x-Aω^2sin(ωt) ここで ω0<<ω の場合を考えてみましょう. この場合,右辺第1項を無視することができるので次のようになります. d^2x/dt^2=-Aω^2sin(ωt) これは,おもりの加速度が支点の加速度に等しいことを意味するので,おもりは支点と同じ運動をすることになります. ところが ω0<<ω というのは,おもりの固有振動数よりもはるかに大きい振動数で支点を振動させるということです.実際にやってみればわかるように,おもりをつるしたばねの上端をすばやく振動させたときは,おもりはつりあいの位置からほとんど動かず,上端の振動と同じ振動をすることはありません. 従って?式は正しくないと思います.
Re: バネの上端を動かす問題
なんとなく さんのレス (2006/07/13(Thu) 15:02)
こんにちは.
レスを有難うございます.するどい御指摘だと思います.上端をすばやく動かしたときの,おもりがほとんど停留状態になる現象は知っていましたし,物理的に面白いことです.これは,おもりにかかる「力」がAsin(ωt)のときの解, x=C0cos(ω0t+α)+Aω0^2/(ω0^2-ω^2)・sin(ωt)・・・? において,(ω0<<ω)の場合第二項〜0となり,第一項〜ゆるやかな振動として説明される現象であると思います. 今の場合,「変位」がAsin(ωt)の解は x=C0cos(ω0t+α)+Aω^2/(ω0^2-ω^2)・sin(ωt)・・・? となりますが,?と?の似て非なる現象が混乱を齎しているのだと思います. ?の場合,強制力の角速度が大きくなっても,強制力の大きさ自体は,ばねの固有振動数ω0に規定された一定値以下です.しかし,?の場合,変位を式どおりに保とうとすれば,角速度ω(の2乗)とともに強制力の大きさが増大していきます.このような場合,系全体が大きく振動し,振動の主体は外部振動に取り代わられるものと思います. yamaさんの御指摘は小さくすばやく動かす,?のケースで生じるものと思います. では,?の物理的現象はなにか.建物の固有振動とそれに対する地震波振動数などがそれにあたるかもしれませんね(これはテキトーです).
Re: バネの上端を動かす問題
yama さんのレス (2006/07/13(Thu) 21:21)
>?の場合,変位を式どおりに保とうとすれば,角速度ω(の2乗)とともに強制力の大きさが増大していきます.このような場合,系全体が大きく振動し,振動の主体は外部振動に取り代わられるものと思います.
その通りですね.しかし実際にはばねの上端をすばやく動かしてもこんなことはおこりません.ということは,実際の運動は?の場合ではないことになります. ?はなんとなくさんが導かれた運動方程式 md^2x/dt^2=-kx-mAω^2sin(ωt) の解なので,その解が実際と合わないということは,この運動方程式が正しくないということだと思います.
>yamaさんの御指摘は小さくすばやく動かす,?のケースで生じるものと思います.
その通りだと思います.ただし,?は「おもりにかかる「力」がAsin(ωt)のときの解」ではありません.計算してみれば分かるように,これは「おもりにかかる「力」が mAω0^2sin(ωt) のときの解」です. このときの運動方程式は md^2x/dt^2=-kx-mAω0^2sin(ωt) ですが,ω0^2=k/m を用いると md^2x/dt^2=-k(x-Asin(ωt)) になることがわかります. これは,おもりにはたらく力が -k(x-Asin(ωt)) になるということで,No.10229 で私が述べたことに一致します. なお,「おもりにかかる「力」がAsin(ωt)のときの解」は, x=C0cos(ω0t+α)+A/(m(ω0^2-ω^2))・sin(ωt) となり,係数が違いますが,運動の性質は?の場合と似たものになると思います.
Re: バネの上端を動かす問題
なんとなく さんのレス (2006/07/13(Thu) 23:21)
>yamaさん. 丁寧に見て頂いて恐縮です. 式の導出はyamaさんの言われるとおりです.うっかりして間違えました.すみません. 正直言えば,混乱しているのは自分の方ですが,バネ上端の「変位」が正弦振動の場合の運動方程式,及びその解は,私が考えたものではなく,「共立物理学公式」力学p4〜5の1.3.3 強制振動を参考にしたものです. もしかすると,私の見方が何か勘違いしているのかも知れませんが.それと,地震の話をテキトーと書きましたが,その後ググッてみると,地震解析の基礎方程式で,地震波による変位の強制振動を扱った記事に出会いましたが,やなり?の運動方程式が使われていて,公式集が間違いとも言えない感じになったわけです.地震解析は勿論バネではありませんが,等価バネと考えているようです. また,これらとは別に「バークレー物理学演習」(M.チェン著陪風館)の力学問題?の4.番に減衰力付きですが,まったく同じシチュエーションの問題があり,その解はmNejiさんやyamaさんと同じです.わたしも学生の頃はこれで学習していたので,なんの疑問も持っていなかったのですが,上記の例により理由を考え直したというのが経緯です. 長くなって申し訳ないのですが,白黒をつけるというような意味ではなく,混乱の原因を詳かにしたいと思いますので,もう少しお付き合い願えると嬉しいのですが.上記図書を入手するのは大変でしょうから,こちらで見て頂けるよう準備すれば,評価して貰えるでしょうか?失礼ながら実力は十分拝見しましたので,御意見を聞かせて欲しいと思っています.準備に2〜3日かかりますが,もし不都合なら止めます.如何でしょう?
Re: バネの上端を動かす問題
yama さんのレス (2006/07/13(Thu) 23:53)
上下動を記録する地震計は,ばね振り子を用いていて,振り子の固有振動数より大きい振動数の地震波で支点が振動してもおもりがほとんど動かないことを利用していますね.これは?のケースだと思います. ?の運動方程式が使われているとすれば,単純に支点が動く場合とは異なった状況ではないかと思いますが,それについて書かれた資料を示していただければ,検討してみたいと思います.よろしくお願いします.
Re: バネの上端を動かす問題
なんとなく さんのレス (2006/07/13(Thu) 23:58)
ありがとうございます.
最悪,私の老眼が原因で添字を見逃していた,というケースも考えられますが,そのときは笑って許してください. 勝手ながら,よろしくお願いします.
Re: バネの上端を動かす問題
なんとなく さんのレス (2006/07/15(Sat) 20:27)
>yamaさん,こんにちは.
急いで拙い資料ですが,ホームページに載せてみました.
振り返ってみると,事の発端は問題のモデルの妥当性に尽きると思いますが,もともとの問題のレベル,仮定,制限条件など,考えると混乱していたようです. 勿論,弾性限界とか,バネを伝わる音波の速度とか,摩擦や変形エネルギーを理想的に0とした場合でも実際は残る物理的条件はあるでしょうが,どこまでがモデルで,どこまでが正解の範囲か分からなくなっています. たとえばピアノ線を持ち出したのは,ご存知のように(力学で言う)剛体は通常即座に力を伝達し(つまり無限の速度ですね),変位応答は系内で瞬間的に均一化されることを前提とできるわけですが,バネが挟まると,勿論そうは行かない.力学の問題としてはバネであっても,そのような変位を仮定するの(が常識なの)か,それとも,本当は複雑な問題をシンプル化しているのか,原理的(これも定義次第ですが)に正しいのか. とりとめないので,とりあえず,下手な資料ですが御見解をお聞かせください. よろしくお願いします.
URLで正体ばれるかも知れないけれど,大した正体でないので,いいかあ(独り言).
Re: バネの上端を動かす問題
yama さんのレス (2006/07/16(Sun) 00:02)
資料を拝見いたしました. 結論としては,x のとり方が違うだけで,どちらの方程式も正しいと思います.
「共立物理学公式」の図を見ると,ばねの全長が 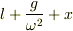 になっています.
になっています. 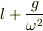 はつりあっているときのばねの長さなので,x は「ばねののび」を表すことになります.
また,振動解析の図3.2では,x は変位とされていますが,これは壁を基準に座標を設定した場合の変位であり,図から分かるように,「ばねののび」に等しくなります.壁自体が動くような座標系における変位ではありません.
はつりあっているときのばねの長さなので,x は「ばねののび」を表すことになります.
また,振動解析の図3.2では,x は変位とされていますが,これは壁を基準に座標を設定した場合の変位であり,図から分かるように,「ばねののび」に等しくなります.壁自体が動くような座標系における変位ではありません.
これに対して,私やmNejiさんは,「ばねののび」ではなく「慣性系におけるおもりの変位」または同じことですが「外力がないときのつりあいの位置からのおもりの変位」を x としています. この場合は,前にも書いたように,ばねののびは x-Asin(ωt) になります. 実際,ばねののびを x としたときの運動方程式 md^2x/dt^2=-kx-mAω^2sin(ωt) において,x を x-Asin(ωt) で置き換えれば,運動方程式は次のようになります. md^2x/dt^2=-k(x-Asin(ωt)) つまり,x の意味が違うだけで,どちらの方程式も同値です.
ただし,hajimeさんの質問に返ってみると,おもりの運動を求めるのが問題だったので,後者の運動方程式を用いるべきだと思います.
Re: バネの上端を動かす問題
なんとなく さんのレス (2006/07/16(Sun) 01:54)
こんばんは.
早速のレス有難うございます.
申し訳ないのですが,正直言って完全に腑に落ちたとは言い難いです. 私の受け取り方に問題が有るかもしれなので,最後にいくつか確認しておきたいのですが.
(1) 共立公式の図は確かに平衡点からの変位は「ばねののび」である. (補足すると,l+g/ωは重力下の自然長.xはそこからの変位ですね) (2) 地震図3.2の変位は,「ばねののび」でこれも自然長からの変位である. (台が振動していようがいまいが,変位とは相対位地差であり,同じだとおもいますが) (3) それに対して,yamaさんやmNejiさんのxは「ばねののび」ではなく,「おもりの平衡点からの変位」である. ここで,「だから,(1),(2)と(3)は異なるモデル化である(要はxの意味が違う) という結論だと思ったら,
>実際,ばねののびを x としたときの運動方程式 >md^2x/dt^2=-kx-mAω^2sin(ωt)・・・? >において,x を x-Asin(ωt) で置き換えれば,運動方程式は次のようになり >す. >md^2x/dt^2=-k(x-Asin(ωt)) ・・・? >つまり,x の意味が違うだけで,どちらの方程式も同値です.
とのことなので,??です.これが同値では結果の違いが説明できません.
前回の議論までは,?のk/m=ω0^2で,?,?はあきらかに同値ではない,という主張だったと思うのですが.実際,変数変換のみでは式は移り変わりません. また,変位はどの問題でもおもりの変位のことですし,運動方程式はあくまで,重りのそれ(だと思うの)ですが.
私としては,単振動しているバネ振動の支点をAin(ωt)で動かした場合,なぜ,変位がxからx-Asin(ωt)になるのか,その確たる説明があれば良いのですが. あと,欲を言えば,強制振動と同じ加速度系から見た場合,どう見えるとお考えかを知りたいです.その見かけの力は慣性系とどう整合するのでしょうか. これを最後の質問にしたいと思います.かなりお手間をとらせたのと,他で質問してマルチポストは避けたいので(もとの問題とかけ離れた感がありますし,いろんな方の意見も伺いたいので,くれぐれもお気をわるくされないよう,お願い致します).
Re: バネの上端を動かす問題
yama さんのレス (2006/07/16(Sun) 12:49)
異なる物理量を同じ文字で表わしたのために,混乱が生じたようなので,別の文字で表して説明します. 簡単のためばねの上端が支点であると考えます.支点もおもりも動いていないときのおもりの位置を原点Oとします.このとき支点からOまでの距離がLであるとします.Oは地面に対して動かないものとし,そこから下向きに座標 x をとります.この座標系 K は慣性系であり,このK系においては支点が動くことになります. 次に支点からLだけ下の点が常に原点O'になっていて,下向きに座標 X をとるような座標系K'を考えます.この座標系では原点と支点の距離が一定(L)なので支点は動かないことになります.これは非慣性系です.このK'系では,おもりの座標 X は,ばねののび(つりあいの長さからののび)に等しくなります. 支点が動いていないときはOとO'は一致していますが,支点が動いているときは一意せず,OO'=Asin(ωt) になります.図を描いてみればわかるように,x とX の間には x=X+OO'=X+Asin(ωt) または同じことですが X=x-Asin(ωt) の関係が成り立ちます.
まず慣性系Kでの運動方程式を考えます.はたらく力は,ばねののびに比例した復元力(ばねの力と重力の合力)だけです.ばねののびはK'系ではXですが,K系では上に書いたように x-Asin(ωt) になります. 従って運動方程式は md^2x/dt^2=-k(x-Asin(ωt)) になります. これは md^2x/dt^2=-kx+mAω0^2sin(ωt) と表すこともできます.ここで ω0^2=k/m です.
K'系での運動方程式は,K系での運動方程式で x=X+Asin(ωt) と置けば得られ,次のようになります. md^2X/dt^2=-kX+mAω^2sin(ωt) (No.10555に書いた運動方程式は右辺第2項の符号が間違っていたことをお詫びします.) この運動方程式は次のように解釈することができます. 支点が動いていないときは右辺第2項は0になるので,普通の単振動です. 外部から見て支点が動く場合も,このK'系では支点は動きません,しかし,K'系自身が加速度運動をするので,慣性力がはたらきます. この慣性力が右辺第2項です.つまり慣性力によって強制振動がおこるわけです. K'系は強制振動と同じ加速度系です. 従って上記の説明が「強制振動と同じ加速度系から見た場合,どう見えるとお考えかを知りたいです.その見かけの力は慣性系とどう整合するのでしょうか.」という質問に対する回答です.
次に,それぞれの方程式の解について考察します. K系での運動方程式の解は x=C0cos(ω0t+α)+Aω0^2/(ω0^2-ω^2)・sin(ωt) です. K'系での運動方程式の解は上の式で x=X+Asin(ωt) と置いたものになり, X=C0cos(ω0t+α)+Aω^2/(ω0^2-ω^2)・sin(ωt) です. x と X は意味が違うので,異なる形の解になっているのは当然ですが,これは座標系の違いによる見かけ上のものです. 前に考察したように ω0<<ω の場合を考えましょう. この場合K系での解では,右辺第2項が無視できるので,支点の運動の影響は無視できて,支点が動かない場合とほぼ同じ振動をすることになります.特に C0=0 になるような初期条件の下では,x≒0 になり,おもりはほとんど動きません.これはおもりが静止しているときにばねの上端をすばやく振動させてもおもりはほとんど動かないという事実と一致します. しかし,おもりは動かなくてもばねの上端は振幅Aで振動するので,ばねののびはほぼ±A の範囲で変化します. ばねののびは,K'系では X に等しいので,X も±A の範囲で変化します. 実際,K'系での解で,C0=0,ω0<<ω と置くと,X≒Asin(ωt) になります. K系でほぼ静止しているおもりを,K系に対して運動しているK'系から見れば動いて見えるのは当然のことです.
>台が振動していようがいまいが,変位とは相対位地差であり,同じだとおもいますが
変位とは位置の変化であり,位置は座標で表されるので,座標系によって変位は違ってきます.台が振動する場合,台に固定した座標系と,地面に固定した座標系では変位は異なります. たとえば,ばねが非常に強くて伸び縮みしない場合は,おもりは台に対して動かないので台に固定した座標系では変位は常に0です.しかし,台が動くと,おもりは地面に対して動くことになるので,地面に固定した座標系では変位は0ではありません.
Re: バネの上端を動かす問題
なんとなく さんのレス (2006/07/16(Sun) 15:58)
なんとなくです.
どうしても文章の不足や,意味の伝達の不完全さを感じてしまいますが,本当に丁寧に解説していただいたことはとても感謝いたします.
書かれた内容もそのとおりだと思います. つまり,問題にしている2式のxにあたる物理量(変位ということばを使いましたが)が,やはり,別物であった(さらに記述している座標系が異なっていた)ということならば,初めから問題に感じなかったと思うのです.
語弊があるといけないので,あえて単純化して書きますが, 「結局,どちらの方程式も,同じ現象を異なる座標系と異なる変位で表しているものである.その意味で,どちらが間違いというものではない. ただし,問題の性質や内容から考えて,静止(慣性)座標系での表現が普通であり,解(の表現)もそのような座標系でのものが期待され,一般的である.」 が結論でよろしいでしょうか.(最後の質問と言いながら,質問形式になってすみません) 私の結論はそうです.
ここからは,勝手な想像,解釈なので読み捨てて頂いて結構なのですが,2点あります.1点はyamaさんが設定された,図を描いてみればわかるOO'=Asin(ωt)というのは,疑う余地は無いのかということです.勿論,この意味は,両座標を比べたとき疑う余地のないのは,支点の位置の振動Asin(ωt)であって,原点O,O'も同じとは限らない(それを言い出せば違う問題だ,というのは承知です)と疑わねばならないこと.2点目は変位についてですが,これはおそらく私の語感が間違っているのでしょうが,物理でいう変位は多分,displacementですよね.異なる座標系どうしで座標を比較してdisplacementを使うのでしょうか.私の感覚では変位とは位置ベクトル差であり,その意味で座標系によらない,のつもりだったのですが.
また長文になりましたが,おかげでもう他に質問する必要のないほど,問題の本質は分かりました(と思います).有難うございました.
それにしても,物理公式(本),なんでわざわざこんな式を(ぶつぶつ・・・独り言).
Re: バネの上端を動かす問題
yama さんのレス (2006/07/16(Sun) 18:25)
なんとなくさんの結論でいいと思います.
OO'=Asin(ωt) については次のように考えてはどうでしょうか. 支点が動いていないときの支点の位置をPとします. このとき,Lの定義により PO=L です. 支点が動いているとき,時刻tのときの支点の位置をP'とします. このとき,P'O'=L です.こうなるようにO'を定義したからです. 従って次の関係式が成り立ちます. PP'+P'O=PO=L P'O+OO'=P'O'=L これらの式の差をとると OO'=PP' が得られます. PP'=Asin(ωt) を代入すれば OO'=Asin(ωt) となります.
Re: バネの上端を動かす問題
yama さんのレス (2006/07/16(Sun) 18:51)
なお,地震による振動の場合,地面に対する建物の振動を考えることが多いのではないでしょうか. その場合は,地面に固定した座標系で考えるとすると,その座標系は非慣性系になりますね.
Re: バネの上端を動かす問題
なんとなく さんのレス (2006/07/16(Sun) 20:23)
>yamaさん,こんにちは.
おかげで,疑問点も整理がついて,今は最早消えました. 折角続けて頂いているので,もう少し勝手なおしゃべりをさせて下さいね.
原点OO'の話は納得していないのではなく,"L"をそのような"定義"として捉えることも別に問題があると思っているわけではありません. 私が言いたかったのは可能性の問題で,本問とは直接関わりがあるかどうか微妙ですが,例えば数mのバネの上端を正弦振動させても,おそらく定常運動になるまでは振動が重りまで伝わるのに有限な速度(時間)を要し,過渡的にはあり得るだろうくらいの意味です.逆に,定常運動を調べる問題であるので,ナンセンスとお思いかも知れませんが,何でも疑ってみるというのが私のスタンスです.その意味で,別の物理現象が隠れていないか,もっと基本的な式がないのかを探りたいという欲求?の現れです.勿論,問題はある種,出題側と受け取り側に共通のコンセンサスが必要であり,その暗黙的条件下で解答するのがマナーとしてなければ意味を為さないこともあると認識していますが,それには多分賛同して頂けると思います.私としては技術的な問題ではなく,物理として抽出すべきエッセンスと言うか,本質を理解したい,という気持ちです.
地震や振動解析の強制振動方程式の導出は,勿論,専門的に研究されている方々のそれぞれの流儀で多少異なるようですが,確かに(揺れる)地面に固定と考えねば,何を計算すべきか直感的に分かり難いですよね.
ちょっと的外れかも知れませんが,上記方々の式の導出方法は私には「工学的」に見えます.ものすごく偏見ですが,「物理的」でない別の匂いがします.この感覚はあまり賛同して頂けないでしょうが,間違っているではなく,「なーんかちがう」.勿論,どちらが上等とかいうことは一切ありません.「なじみ」の問題です. その理由は定義も含めて,不問として下さい(^o^;).
あらためて,有難うございました.では,また.
Re: バネの上端を動かす問題
yama さんのレス (2006/07/16(Sun) 20:59)
確かに,現実の物理現象と,その理想化・単純化されたモデルの間には当然違いがあるはずですね.そのモデルが何を取り入れ,何を切り捨てているかを認識しつつ,モデルの適用限界を考えることが大切だと思います.
工学についてはよく分かりませんが,たとえば,物理と化学で同じ問題を扱っても,その扱い方が微妙に違っていたりしますね. それは,それぞれの学問分野の特質とか,歴史的な経緯とかが背景にあるのだと思いますが・・・その違いにちょっととまどうことはありますね.
Re: バネの上端を動かす問題
yama さんのレス (2006/07/18(Tue) 10:28)
No.10225でmNejiさんが書かれた内容を読み返してみると,ちょっと疑問に思うところが出てきました. 書いてある内容自体が間違っているというわけではありませんが,問題の題意に合っていないのではないかという疑問です.
まず,問題では「上端oを上下に動かし,Asinwtで表される振動をさせるとき」となっているので,上端の座標X0が X0=Asinwt のように変化するのだと思うのですが,mNejiさんは,
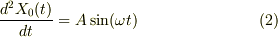 と書かれているので,これでは上端の加速度が Asinwt ということになります.
(
と書かれているので,これでは上端の加速度が Asinwt ということになります.
( 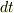 は
は 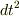 の誤りだと思います.)
の誤りだと思います.)
次に,mNejiさんが導かれた運動方程式
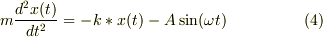 は,慣性系での運動方程式だと思っていましたが,よく読み直すと,エレベータに固定された非慣性系での運動方程式のようですね.上端の座標がAsinwt の場合は上端の加速度は -Aw^2sinwt になるので,mNeji さんの運動方程式の A を -Aw^2 で置き換えれば,私が No.10575 で書いたK'系(非慣性系)での運動方程式に一致します.
確かに,振動するエレベータに観測者が乗っていて天井からばねで吊り下げられたおもりを観測する場合は,この方程式でいいと思います.この場合は,ばねの上端は観測者から見れば動きません.
しかし,問題文からは,ばねの上端は観測者から見て振動するように読み取れます.
たとえば,観測者が,ばねの上端を手で動かして振動させるとか,何かの機械でばねの上端を振動させ,そのときのおもりの運動を観測するというような状況です.
このような場合は,慣性系で運動を考えるのが普通ではないでしょうか.
は,慣性系での運動方程式だと思っていましたが,よく読み直すと,エレベータに固定された非慣性系での運動方程式のようですね.上端の座標がAsinwt の場合は上端の加速度は -Aw^2sinwt になるので,mNeji さんの運動方程式の A を -Aw^2 で置き換えれば,私が No.10575 で書いたK'系(非慣性系)での運動方程式に一致します.
確かに,振動するエレベータに観測者が乗っていて天井からばねで吊り下げられたおもりを観測する場合は,この方程式でいいと思います.この場合は,ばねの上端は観測者から見れば動きません.
しかし,問題文からは,ばねの上端は観測者から見て振動するように読み取れます.
たとえば,観測者が,ばねの上端を手で動かして振動させるとか,何かの機械でばねの上端を振動させ,そのときのおもりの運動を観測するというような状況です.
このような場合は,慣性系で運動を考えるのが普通ではないでしょうか.
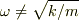 の間違いでは?
の間違いでは?