みや さんの書込 (2006/07/06(Thu) 01:37)

はじめまして． 大学１年で物理を習っているみやといいます．

早速質問なんですが

先日，液体架橋の実験計算でラプラスの式を使ったので ラプラスの式の導出をしようとしたのですが 本を調べても速度ポテンシャル，連続の式を使うものしかでてこず，目的の

Δp=σ((1/R1)+(1/R2)) p=圧力σ=張力 R1，R2=任意の界面の曲率半径

の形のラプラスの式をどうやっても導出することができませんでした． どなたか教えていただけないでしょうか よろしくお願いいたします．

toorisugari no Hiro さんのレス (2006/07/06(Thu) 04:00)

> Δp=σ((1/R1)+(1/R2))

Δってラプラシアンかと思ったので，「こんな難しいの1年で習うの?」と驚きましたが，単に界面を挟んだふたつの流体の圧力( 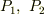)の差 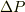( 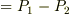:ラプラス圧)のことだったんですね．

それでも表面張力の導出や2次元曲面の平均曲率を1回生にわかりやすく説明する力量はないので，直感的な(いい加減な)説明で勘弁してください．

平面状のシャボン膜はいくら面積を縮めようとする「張力」が働いても界面の両側に圧力差は生みません．

でも球状のシャボン膜(シャボン玉)は張力のおかげで玉の内部の圧力が若干，大気圧より高くなります．

すなわち面が曲がることで張力が圧力差を生みます．

平面は半径無限大の球面の一部と考えれば，圧力差が，平面では0，球面では非0となるような簡単な構成は

圧力差=2*比例係数/半径

と考えられます(2はおまじないです)．比例係数をとりあえず表面張力係数と呼びましょう．

実際の曲面は球面の一部とは考えられない(楕円体のように，もっともぴったり内接する円の半径が縦横方向で異なる)のでややこしいですが，それぞれの方向の半径から計算される圧力差の平均がラプラス圧になると予想すれば

ラプラス圧 = 表面張力係数*( 1/(半径1) + 1/(半径2) )

が求める答えとなります．

表面張力をきちんと導きだしたいのでしたら，熱力学の教科書，たとえば，ランダウリフシッツ統計力学15章など，をみてください．

また，ラプラス圧の丁寧な説明は

• http://www.agr.hokudai.ac.jp/env/soilamelio/teambibai/soilwater/retentio/3tension/laplace/laplace.htm

をみてください．

みや さんのレス (2006/07/06(Thu) 18:23)

ラプラス圧の導出の概念がすごくよくわかりました． toorisugari no Hiroさん本当にどうもありがとうございます．

もう少しよく知りたかったのでランダウ，リフシッツ統計物理学の15章の界面のところを読んだのですがちょっと難しくて導き出すことはできませんでした．すみません．

でもせっかく教えていただいたのでできるだけ頑張ってみます．

toorisugari no Hiro さんのレス (2006/07/06(Thu) 22:02)

みやさん

> もう少しよく知りたかったのでランダウ，リフシッツ統計物理学の15章の界面のところを読んだのですがちょっと難しくて導き出すことはできませんでした．

もっと簡単なテキストを紹介できれば良かったのですが，手元で記載してるのがあの本(名称不正確でした．ごめんなさい)しかなかったのでした．

要点を乱暴にかみくだくとこんな感じです． (1) 圧力に面積をかけることで，その面を介して作用する力が得られます．

2. 力×道のりは仕事ですし，面積×道のりは体積変化ですから，圧力 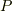のもと体積を 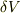だけ増やしたときの「圧力」がした仕事は

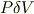
になります．

3. アナロジーから，界面の「張力」が面積を 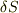だけ増やしたときの仕事は

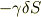
とするのが自然です．この 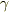を表面張力と呼びます． (張力と圧力で符号が違うのは片方が引く作用，片方が押す作用だからです．）

というところでしょうか．

(2)(3)の量はともに同じ「仕事」の次元を持つ量だから，表面張力 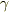は「圧力*長さ」の次元をもつことがわかります．

ですから，圧力差=2*表面張力/半径という仮定はもっともなことがわかります．(係数の2は自由エネルギーの微分で導出してるので説明は勘弁．でも直感的には面は「2」次元だからで良いと思います．)

(1)のアナロジーから，界面内の線分を介して作用する「張力」由来の力(線分に垂直な界面内の方向にベクトルが向きます)の大きさは「表面張力*長さ」で与えるのが自然でしょう．これを使ったラプラスの式の丁寧な導出が上で紹介したURLにありますので参考にしてください．（ここから係数の2も説明できます．)

みや さんのレス (2006/07/07(Fri) 16:31)

toorisugari no Hiroさんのおかげで無事導出することができました． 紹介したいただいたURLもすごく参考になりました． ありがとうございました．

まとめをしないといけないのですが実力不足のためきれいな導出はできていません．なので参考にした本とWebサイトを書くことでまとめにかえさせていただきます．

• http://www.agr.hokudai.ac.jp/env/soilamelio/teambibai/soilwater/retentio/3tension/laplace/laplace.htm
• http://www.lowtem.hokudai.ac.jp/ptdice/ogawa/data/MS.doc

ランダウ，リフシッツ統計物理学

物理化学朝倉書店

toorisugari no Hiro さんのレス (2006/07/08(Sat) 19:37)

> 無事導出することができました．

よかったです．

> まとめをしないといけないのですが実力不足のためきれいな導出はできていません．

:-)こんど，同じような質問があったときにみやさんがたすけてあげてください．

そういえば，みやさんの紹介されたdocumentをみていたら，定本の 「久保亮五 大学演習 熱学・統計力学」 にも解説があることに気がつきました．見落としていました．_o_