２年生 さんの書込 (2006/07/05(Wed) 16:02)

こんにちは． 最小作用の原理による力学だと，質点は「始点と終点を決めたとき，ラグランジアンの時間積分が最小になるような」軌道を実際に通るらしいですが，その最小になる条件，ラグランジュ方程式は運動方程式と同値なのですよね？ ということは初期条件が必要ですよね？ なぜ，始点と終点が決まっていて，速度もラグランジアンが最小になるように調整された速度と決まっているのに，初期条件が必要なのでしょうか？もう，位置も速度も与えられているのではないのですか？

mNeji さんのレス (2006/07/05(Wed) 17:19)

手元に解析力学の解説書が無いので詳しい説明は出来ませんが...．

荒っぽく言ってしまえば，解析力学は「ニュートンの運動方程式がすくに解らないような複雑な系の解析が出来るように考えられた」と理解すれば良いと思います．

ご存知のようにニュートンの運動方程式と万有引力の法則により，2体系の問題は，とても美しい一般解(楕円，双曲線，放物線)に成功したものの，3体系では，とても特殊な解(三角形，一直線：うろ覚え)がせいぜいで，多体形を含む森羅万象を解析する手段にはならないという認識があったのだと思います．

そのうえ，量子力学の伸展にともない，座標と運動量との関係を抽象化する数学的基盤を作る為に，ある意味で「人為的な計算手段」として解析力学が生まれたのだと思います．

と，言うのは，私の偏見だけかもしれませんが...でも，最近，偶然から，ロボット工学での「腕や脚の記述」を調べていると，ラグラジアンだとかハミルトン形式の云々と，解析力学のオンパレードであることを知り，驚愕すると共に，「人為的な計算手段」と片付けていた自分が恥ずかしくなりました．

前置きが長くなりました．本当は，Johさんに綺麗な図と式で説明をお願いしたいところです．

簡単にいえば，

「ある座標と共役の位相空間で，点Aから点Bへの運動を考える」と言うだけの束縛，言い換えるときに初期条件Aと終了条件Bが決まった時に，ラグラジアン;その粒子の「運動エネルギー」と「ポテンシャル・エネルギー」の差分の経路積分を最小にする経路に課せられる条件を考えるという，公理的な問題提起している．

のであって「初期条件から運動方程式に従って，逐次積分的に運動は決まる」という視点では無いと思います．

ついては，変数の微分ではなく，関数の変分みたいな抽象的な差分の検討が始まる...むにゃ・むみゃ．．．おおい，Johさ〜ん...

取り急ぎ，解析力学の生み出る時点の感触について．老人の出番は，ここまで．

yama さんのレス (2006/07/05(Wed) 23:19)

２年生さん，こんばんは． ２年生さんは．運動方程式には初期条件が必要だと誤解されているようですが，そうではありません． 運動方程式は微分方程式なので，一般解は任意定数を含んでいます．初期条件が与えられている場合には，その初期条件を満たすように任意定数の値を定めれば運動が決まるということは承知のことと思います． しかし，任意定数を定める条件が必ず初期条件の形で与えられるわけではありません．一般には，境界条件を満たすように任意定数の値を決めます．もちろん初期条件も境界条件の一種ですが，初期条件でない境界条件もあります． 一つの時刻の座標と速度を指定するのが初期条件ですが，そのかわりに２つの時刻の座標を指定することもできます．それによっても任意定数の値が決まるので，運動も決まります．この場合，運動方程式を解いた結果として速度も決まるわけですが，あくまでも解いた結果として決まるわけで，解く前から初速度がわかっているわけではありません．

２年生 さんのレス (2006/07/06(Thu) 00:24)

＞mNejiさん 詳しいご回答ありがとうございます．工学でも使われているんですね． ＞yamaさん ＞そのかわりに２つの時刻の座標を指定することもできます． 最小作用の問題では，始点と終点を固定しますよね？ ということは，２つの時刻の座標がすでに与えられているのではないのですか？ しかし，変形して得られたラグランジュ方程式にはまた，さらに２つの任意定数を消す条件が必要になりますよね？それはなぜなのでしょうか？ つまり，境界条件が普通の運動方程式の倍，必要になってませんか？

２年生 さんのレス (2006/07/06(Thu) 00:28)

それと，運動方程式の解に任意定数が２つ入ってくるのは，例えばボールを投げたとしたら，放物線になるのは運動方程式によって決定されるが，どんな放物線を書くかはわからないから何か条件が必要になってくるわけですよね？ しかし，最小作用の場合は，「作用が最小になるような軌道」を求めることから出発したわけで，それの解は即座に，求めたい軌道になっていなければおかしいのではないのでしょうか？

mNeji さんのレス (2006/07/06(Thu) 01:27)

いわゆる，ハミルトンの原理は，

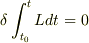
を要請した場合に，ラグラジェアン にどのような(微分)方程式が成立するかだけを問題にしていますね．

ニュートンの運動方程式でも，質点がどんな運動環境，たとえば； ・真空中で重力場だけで運動する場合 ・水中で流体力学とコリオリ力の影響で動く場合 ・真空中で電磁場が伝播してる場合 とかが決まれば，運動方程式は一意的に与えることができます．

ところが，一般解を解かなくても，微分方程式の一部に保存する量が出てくる場合には， ・角運動量保存(面積速度一定) ・エネルギー保存則 ・光子には縦波成分が存在しない（いい例では無いかも） が判る場合もあります．

もち論，ニュートン流の運動方程式でも，ラグランジェの運動方程式でも，ハミルトンの運動方程式でも，一般解を解く場合には，それらの自由度に応じた初期条件がいるのには変わりませんね．

ｙama さんのレス (2006/07/06(Thu) 09:34)

>最小作用の問題では，始点と終点を固定しますよね？ >ということは，２つの時刻の座標がすでに与えられているのではないのですか？ >しかし，変形して得られたラグランジュ方程式にはまた，さらに２つの任意定数を消す条件が必要になりますよね？それはなぜなのでしょうか？

変形して得られたラグランジュ方程式が無条件でもとの最小作用の原理と同値になるわけではありません． ラグランジュ方程式に境界条件（２つの時刻の座標値）を加えたものが，最小作用の原理と同値になります． つまり，ラグランジュ方程式自体は境界条件の情報を含んでいないため，別に境界条件を付け加える必要があるわけです． 境界条件を指定しないでラグランジュ方程式を解くと，任意定数を含む一般解が得られますが，境界条件を与えるとその任意定数が決まるわけです． しかし，この場合の境界条件としては，必ずしも２つの時刻の座標である必要はなく，１つの時刻の座標と速度でもかまわいません． そういう意味では，与えられた初期条件の下での運動を求めるには，最小作用の原理を用いるよりも，それから導かれたラグランジュ方程式を用いるほうが都合がいいわけです． なお，2つの時刻の座標と初期条件を同時に与えた場合は，それらを同時に満たす解は一般には存在しません．どちらか一方だけで解は完全に決まります． 従って境界条件が普通の運動方程式の倍，必要になることはありません．

>それと，運動方程式の解に任意定数が２つ入ってくるのは，例えばボールを投げたとしたら，放物線になるのは運動方程式によって決定されるが，どんな放物線を書くかはわからないから何か条件が必要になってくるわけですよね？ >しかし，最小作用の場合は，「作用が最小になるような軌道」を求めることから出発したわけで，それの解は即座に，求めたい軌道になっていなければおかしいのではないのでしょうか？

２つの時刻のボールの位置を境界条件として，その境界条件を満たすように運動方程式の一般解の任意定数の値を決めれば，ボールの軌道は完全に決まります． 同様に，２つの時刻のボールの位置を指定して最小作用の原理を適用すればボールの軌道は完全に決まります．

２年生 さんのレス (2006/07/06(Thu) 22:05)

ということは，最初の前提「始点と終点を固定，つまり，t0とtのときの位置という条件」は，最小作用の原理からラグランジュ方程式を導いたときに「消えて」しまって，ラグランジュ方程式は「始点と終点を固定していた」という情報を失ってしまった，ということでしょうか？ ＞２つの時刻のボールの位置を指定して最小作用の原理を適用すればボールの軌道＞は完全に決まります． 条件を失わないように，最小作用の原理から方程式を導くことが出来るのですか？

yama さんのレス (2006/07/07(Fri) 00:08)

>ということは，最初の前提「始点と終点を固定，つまり，t0とtのときの位置という条件」は，最小作用の原理からラグランジュ方程式を導いたときに「消えて」しまって，ラグランジュ方程式は「始点と終点を固定していた」という情報を失ってしまった，ということでしょうか？

そういうことだと思います．ラグランジュ方程式は特定の始点と終点に対してだけ成り立つのではなく，始点と終点をどのように選んでも一般的に成り立つ式だからです．

>条件を失わないように，最小作用の原理から方程式を導くことが出来るのですか？

最小作用の原理によって，ボールの軌道が完全に決まるというのは，最小作用の原理を満たす解がただ１つ存在するということです．つまり解の存在と一意性について述べたわけです． 実際に計算する場合は，結局はラグランジュ方程式に帰着するので，境界条件を考えないといけません． ただし，近似解でよいなら，いくつかのパラメータを含む試行関数を用いて作用積分が最小になるようにパラメータの値を決めることができます．それによって近似解が一意的に定まります．

２年生 さんのレス (2006/07/08(Sat) 03:18)

よかったです．謎が解けました．ありがとうございました． 思えばラグランジュ方程式はただ極値の条件式にすぎないわけですからね．あたりまえでした．最小作用の原理はもっととてつもなく大きいもののように感じます．

＞近似解でよいなら，いくつかのパラメータを含む試行関数を用いて作用積分が最小になるようにパラメータの値を決めることができます コンピューターで直接求めるということですね．