固有振動
固有振動
カリプソ さんの書込 (2006/07/03(Mon) 17:55)
ご無沙汰しております.前回の質問がまだ整理がつかないまま質問することになりますが,宜しくお願いします.前回ご返答いただいたものに関しても取りかかろうかというとこなので,(体調を崩しておりました・・・)また疑問がでてきた時は宜しくお願いします. さて,今回の質問なのですが,「両端が開口端気柱(開管)の固有振動を3倍振動まで求めよ.」と宿題を課せられたのですが,「固有振動」とは波のことをいうのですよね??答え方としては波の式を記述すればよいのでしょうか?それとも図を書けということなのでしょうか?? 宜しくお願いします.
Re: 固有振動
mNeji さんのレス (2006/07/04(Tue) 01:59)
一番簡単な説明をしてみます.
30cmぐらいの定規をお持ちですか?
その中央を「示指」と「母指」とで挟みます.そして軽く左右に回転させるとどうなるでしょうか?
中央部は殆ど動かずに, ・左側が下がれば右側が上がり, ・右側が下がれば左側が上がり, 以下この繰り返しです.
開菅の両端は,こんなイメージでしょう.これを定常波の用語で言えば, ・左端は「腹」 ・中央部は「節」 ・右端は「腹」
一種の基底(一次)振動とも言える波動モードでしょうね.
「腹」と「節」は交互でないと定常波になれず,両端は題意より「腹」です.また「腹」と「節」の距離は,定常波の波長  の4分の一,
の4分の一, 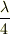 です.
です.
とすると,先に述べた基底振動の菅の長さ  は,
は, 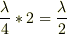 ,半波長に対応します.TVやFMのアンテナなどはこのタイプだとおもいます.
,半波長に対応します.TVやFMのアンテナなどはこのタイプだとおもいます.
すると2次振動では;
・左端は「腹」 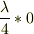 ・次は「節」
・次は「節」 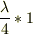 ・次は「腹」
・次は「腹」 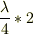 ・次は「節」
・次は「節」 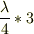 ・右端は「腹」
・右端は「腹」 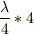
従って,同様にしてn次振動の時,は 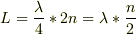 ですね.
ですね.
もし振動数を出したいときには,振動数  ,波の速さ
,波の速さ  とすると
とすると
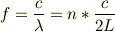
Re: 固有振動
toorisugari no Hiro さんのレス (2006/07/04(Tue) 02:52)
開口端補正って考えなくて良かったんでしたっけ. # どういう計算かは忘れてしまったんですが...
Re: 固有振動
mNeji さんのレス (2006/07/04(Tue) 03:50)
>開口端補正って考えなくて良かったんでしたっけ.
世の中,すべての理論なり計算処方には,ゼロ時近似から出発して,主理論,補正近似とかありますね.
だけれども,初学者さんには基本原理を直裁に感じ取り,そこからなるべく単純に答えを出すことを身に付けたいですよね.
他方,実用技術の側面で言えば,エッジ部の振動は簡単でないのも事実です.今手元に本がありませんが,フルートやオーボエ制作の神様という人は,ホールの大きさ,位置,パイプの直径について,克明な実験をして経験値を割り出したと,書いてあったとおもいます.ベームさんだったような気もしますが...
フルート吹きは,そうでなくても吹き込むにつれて菅の温度が上がるので,適宜長さを調節します,本能的に(笑).
Re: 固有振動
mNeji さんのレス (2006/07/04(Tue) 13:15)
>開口端補正って
友人から,定性的な説明は出来ないか?と突っ込まれました.
波がどの現象:音,電磁化,流体の波, etc;かにも強く依存すると思います.
しかし,音で考えると,開口部で,空気の振幅が大きくなるわけで,菅のエッジよりそとの空気が引きつられて振動します.これは,空気の粘性に起因するとおもいます.
従って,音波では,実際の菅長よりも長めに振舞うと予想されます.
と考えると,電磁場(アンテナ)でも,エッジ周辺の電磁場はアンテナ先端部で一種の回折的に染み出す部分がでてくる,もっともらしく言えば,有限長ので,場が広がるとおもいます. 故に,この場合でも実際のアンテナ長よりも長めに振舞うでしょう.
ちなみに,電子工学の人に聞いたら,アンテナには短縮率という言い方があるそうです.そういわれると,大昔,アマチュア無線でダイポール・アンテナを立てましたが,そんな補正をしたような,しなかったような....
Re: 固有振動
カリプソ さんのレス (2006/07/05(Wed) 16:23)
漠然とした質問で申し訳ありません.ただ,No.10159に記載した問いが教科書にのっていて,それをやってくるよう言われただけだったのでよくわからず投稿したのでした. >「固有振動を求めよ」とは; ・振動モードのこと ・波長のこと ・振動数のこと ・振動波形の一般解? いったい何でしょうか? っということが知りたくて投稿させていただいたのですが,そこは出題者にしかわからないのですね. >管の長さを適当に仮定して,そこに生じる固有振動の波長や振動数を図を書くなりして説明してはどうですか. CO@物理のかぎプロジェクトさんのいうように自分で管の長さを仮定して,波長,固有振動数(速さをvとでもおいて),等をかいて提出しようと思います. >我々は便利屋ではないのです. 申し訳ありません.前述の私が質問していたことは出題者に確認すべきことだったのですね.
Re: 固有振動
CO さんのレス (2006/07/05(Wed) 17:52)
カリプソ さん > >我々は便利屋ではないのです. > 申し訳ありません.前述の私が質問していたことは出題者に確認すべきことだったのですね.
こちらこそ不躾だったかもしれません,すみません.
今回の質問の場合,教科書に載っていた問題とのことですので, 問題の載っている前ページを読めば何を答えれば良いか解るように書いてあるはずです. むしろその教科書を読んでいる人にしか,どう答えれば良いのか正確にはわからなかったと思います. (教科書を引用する場合,出典を書いておくと良いです)