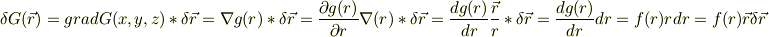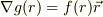無題
無題
hajime さんの書込 (2006/07/02(Sun) 23:48)
もうすぐテストなんですがこの問題は絶対出るんですが,何時間考えても答えが出ません.問題は単純で「中心力は保存力であることを示せ」です
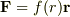 中心力Fは以上のようにあらわせる事を用いれば良いみたいですが.
中心力Fは以上のようにあらわせる事を用いれば良いみたいですが.
Re: 無題
yama さんのレス (2006/07/03(Mon) 00:19)
を極座標で示せばいいと思います.
Re: 無題
hajime さんのレス (2006/07/03(Mon) 00:32)
うーん.rot(ローテーション)とかはまだあまり理解できていないので・・・できたら他の方法をおしえて欲しいのですが.すいません.
Re: 無題
mNeji さんのレス (2006/07/03(Mon) 00:57)
hajimeさん:
始めまして.:P
保存力の定義のうち何を使って証明するかにもよります.
点Aから点Bまでの仕事,
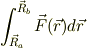
が,半径成分の積分に帰着することから,経路に拠らないので,保存力を主張できます.
ついでに,点Aから点Bの間を何層かの同心円で切り(お菓子のバウムクーヘン),適当に動径方向と,同心方向とを進んだ図を書き,中心力だから同心方向の積分は零をアピール.
追伸:すこしインチキな説明
位置ベクトルの内積を考えて,その微分を考えます
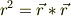
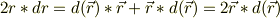
Re: 無題
toorisugari no Hiro さんのレス (2006/07/03(Mon) 18:04)
「中心力は保存力であることを示せ」って文章は問題ありますよね.正確には 「大きさが中心からの距離のみの関数で表される中心力は保存力であることを示せ」 ですよね.ま,式にはそう書いてあるので問題はないですが...
証明としては,任意の関数  について
について
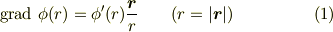
がいえることと, 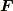 の定義を見比べれば,
の定義を見比べれば, 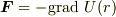 となる
となる  が存在することを示せます.
が存在することを示せます.
(1)式は微分の鎖則と,mNejiさんが最後書かれた式と同じ考え方から導かれる式
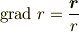
とで示せます.
(前に書いた記事は答えをそのまま書いたことになるので削除しました.)
遅くなりました
hajime さんのレス (2006/07/05(Wed) 15:25)
なぜ
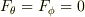 なのですか??
なのですか??
これでどうですかね??
hajime さんのレス (2006/07/05(Wed) 15:49)
よって点A,Bを局座標で考えたとき,P1からP2までに中心力によってされた仕事はrのみよるもので角度には依存しない.これはどの経路を通ってもなされる仕事は等しいので中心力は保存力である.
一応頑張ってといたのですが,間違っていますか??
Re: これでどうですかね??
mNeji さんのレス (2006/07/05(Wed) 16:08)
かなり正解に近づいたとおもいます.積分の中身だけを書けば
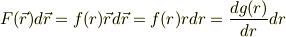
などとしたらいかがですか.
当面は,この積分が意味するところを図形的にじっくり味わっておきましょう.ベクトル解析が詳しく身に付いてくると,各種の積分と偏微分との関係から,保存力にまつわる芳醇な姿が明らかになると思います.
近代物理学のスタート点に立たれたと言えるのでしょうね.
追伸:
toorisugari no Hiroさんの
- 2006/07/03(Mon) 18:04 No.10160
記事の式(1)を念頭に, 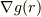 を計算すると,如何ですか.
を計算すると,如何ですか.
Re: これでどうですかね??
yama さんのレス (2006/07/06(Thu) 00:07)
について説明しておきます.
極座標で考えたとき 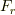 は動径方向の力の成分で,
は動径方向の力の成分で, 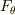 と
と 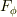 はそれぞれ天頂角方向と方位角方向の力の成分です.中心力なので,動径方向の成分だけがあり,それに垂直な方向の成分は0になるわけです.
なお極座標では,
はそれぞれ天頂角方向と方位角方向の力の成分です.中心力なので,動径方向の成分だけがあり,それに垂直な方向の成分は0になるわけです.
なお極座標では,
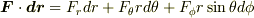 になることに注意しましょう.
になることに注意しましょう.
ありがとうございました.
hajime さんのレス (2006/07/06(Thu) 01:09)
yamaさん,mNejiさんありがとうございました.つまり,
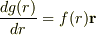 とおけばいいってことですよね.
ベクトルに関してはこれから頑張っていきたいと思います.
とおけばいいってことですよね.
ベクトルに関してはこれから頑張っていきたいと思います.
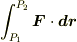 の値が始点と終点のrの値だけで決まることを極座標で示すのはどうでしょうか.
の値が始点と終点のrの値だけで決まることを極座標で示すのはどうでしょうか.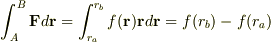
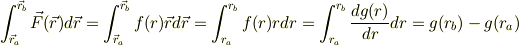
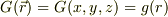 について,微分量を考える;
について,微分量を考える;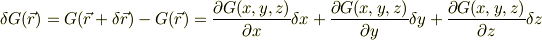
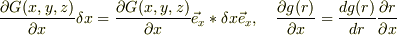 に注意すれば;
に注意すれば;