POTYOMUKIN さんの書込 (2006/07/02(Sun) 10:20)

物体が対数らせん（等角らせん）r=e^(aφ)を描いて運動し，その加速度はつねに原点に向かっている．そのとき，加速度の大きさは距離の3乗に反比例することを示せ．という問題なのですが， 自分はニュ−トン運動方程式より，（書き方が分からないので一回微分をｆ＾[1]としました．） m(r^[2]-r｛φ＾[1]｝＾２＝F・・・・・・? m(rφ＾[2]+2ｒ＾[1]φ＾[1]）＝0・・・・・? r=e^(aφ) ｒ＾[1]＝ae^(aφ)φ＾[1]＝arφ＾[1] ｒ＾[2]＝a^(2)e^(aφ){φ^[1]}^2+ae^(aφ)φ^[2]=a^(2)rφ^[1]^2+arφ^[2] ?に代入 m(rφ^[2]+2arφ^[1]φ^[1])=0 φ＾[2]+2a｛φ＾[1]｝＾2＝0

までやってここから φ＾[1]＝ r＾[1]＝arφ＾[1]＝ ｒ＾[2]＝ で?に代入して F＝ 加速度＝F/ｍ＝ で求めようと方針を立てたのですが，

φ＾[2]+2a｛φ＾[1]｝＾2＝0・・・・? φ＾[1]＝ をもとられそうでうまくいきませんでした．とりあえず変数分離で，φ＾[1]＝ｙとおいて ?は ｙ＾[1]+2ay^2=0 −∫(2a)dt=∫｛1/（ｙ＾2）｝ｄｙ 2at=1/y+cでｃがどうなるのかなんか分かりませんでした． そもそもこの流れであっているのかが疑問です． だれか教えて下さい．お願いします．最終的な答えも教えてくれると助かります．

mNeji さんのレス (2006/07/02(Sun) 13:24)

はじめまして．

>等角らせん）r=e^(aφ)

これは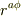， で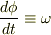， 一定，のこと？

もしそうならば

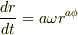
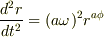
これらを，加速度の動径方向成分に入れるとどうなりますか？

yama さんのレス (2006/07/02(Sun) 13:45)

角速度は一定でないと思います． 加速度がつねに原点に向かっているのですから，角運動量が一定になるはずで，このことは?式から導くことができます．

mNeji さんのレス (2006/07/02(Sun) 14:21)

yamaさん:

なるほど，「等」角に目が行き過ぎたかと思います．反省．

すると，問題の出し方が意地悪いようにおもいます．たとえば

動径rが角度にのみ依存し 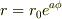で，中心力だけが働くばあいには，中心力 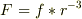であることを示せ．なお 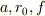は定数とする．

なんとなく さんのレス (2006/07/02(Sun) 15:47)

POTYOMUKINさん，こんにちは．

もう答えを出されている方もいるようなので，あまり出しゃばるのは何ですが．

>そもそもこの流れであっているのかが疑問です． >最終的な答えも教えてくれると助かります．

とのことですし，ご自分でもかなり考えられたようなので，流れのヒントと私の得た答えを書いておきます． 共に考えて頂いている方々への礼儀として，ちゃんとできたら，御報告されるのが宜しいかと・・・．

この問題は力を評価する記述も初期値条件もありませんから，それらの要らない解法が宜しいでしょう．軌道を極座標で表したとき，動径方向への加速度をｒのみの関数として記述すれば答えです． φ方向（の加速度）ベクトルは問題の中に書かれている条件より，「０」です． これはyamaさんが指摘されたとおり，角運動量ｈが保存することを導きます． r=exp(aφ）より，rの微分，角運動量一定の式よりφの微分がすべてｒの関数で表せます． 答えは私の計算が間違っていなければ， 加速度=（a^2・h^2）/(2r^3) (hは上の角運動量）となります． これから，確かに動径方向加速度〜r^-3となります．

ついでに，２番目の問題は，記述に少し混乱が見られる気がしますが，単位質量あたりの角運動量を，ｈ，近日点での太陽までの距離を，ｌ，その近傍まで来たときの太陽までの距離をｒとすれば，加速度はつまり単位質量あたりの，向心力と同じことを意味するので，-(h^2/l)/(r^2)はすなわち，引力です． 積分の必要はありませんが，エネルギー計算の方向はそれで合っていると思います．勿論E'>0なら双曲線ですね． では，がんばって下さい．

mNeji さんのレス (2006/07/02(Sun) 17:33)

POTYOMUKINさん：

確認結果をTexモードで書こうとしたのですが頓挫しました(泣)．

重要なところだけ書きます：

なお，丸に数字のマークはMac系の人では化けるので(1)などが安全です．

さて，(2)をどうするかが鍵です．これは外力の接線方向が無いことを意味しますね．従って，角運動量が保存します．それを反映したのが(2)です．辺々にrをかけて，r^2の時間微分を思い浮かべると；

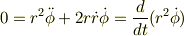
ですから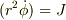

この関係を適宜使って，時間微分項をrで置き換えていけば...．

当然ですが，万有引力，クーロン力は皆，中心力ですから面積速度一定の法則に従いますね．

POTYOMUKIN さんのレス (2006/07/02(Sun) 17:36)

mNejiさん，yamaさん，なんとなくさん返信ありがとうございますおかげでなんとかなりそうです．

ｒ＾[1]＝ae^(aφ)φ＾[1]＝arφ＾[1]・・・・（4） ｒ＾[2]＝a^(2)e^(aφ){φ^[1]}^2+ae^(aφ)φ^[2]=a^(2)rφ^[1]^2+arφ^[2]・・・（5）

r＾（2）φ＾[1]＝ｈ φ＾[1]＝ｈ/r＾2・・・・・（6） をもちいて微分やって（4）からｒ＾[1]＝ah/rより φ＾[2]＝2ｈｒ＾[1]/ｒ＾3＝2ah^2/r^4・・・・・（7）

加速度＝ｒ＾[2]＝3a^(2)h^(2)/r^3 となって一応出ましたが，なんとなくさんの答え加速度=（a^2・h^2）/(2r^3)と違ってしまいました．どこか間違ってますか？

まだ自分はもう一つの問題が全然できていなかったりします．

なんとなく さんのレス (2006/07/02(Sun) 19:40)

こんにちは．

極座標を使った場合，速度はベクトルとして変換されます． 速度ベクトルV=Vx×i+Vy×j(直交座標系，i,jはx,y方向単位ベクトル）は， 極座標系では，V=Vr×ir+Vφ×jφ=r'×ir+rφ'×jφ('は微分)≠r'×ir+φ'×jφ となります．等式の中と右辺の違いは基底ベクトルの変換によるものです． 加速度もベクトルですから，極座標系では， a（加速度)=V'=dVr/dt×ir+Vr×d(ir)/dt+dVφ/dt×iφ+Vφ×d(iφ)/dt

=(r''-rφ'^2)×ir+(1/r)d/dt(r^2φ')×iφ

となります．ここはとても重要なところです．再学習をお勧めしますよ． この式から，前記のように，φ方向加速度=0から， (1/r)d/dt(r^2φ')=0，したがって，r^2φ'=定数（角運動量保存） が出てくるわけです． 以上から，動径(r)方向の加速度は，r''ではなくて，(r''-rφ'^2)を計算しなければなりません． なお，私も計算間違いしていたようで，答えは，-h^2(1+a^2)/r^3のようです． 加速度は動径方向と逆向きですから，（ベクトル的に）負でないとおかしいですね．

楕円の問題に関しては，角運動量の定義から速度を逆算してはどうでしょう． では，また．

POTYOMUKIN さんのレス (2006/07/02(Sun) 20:58)

返信ありがとうございます．じっくり復習しようと思います． （加速度) =-h^2(1+a^2)/r^3とでました．上の（7）を―付け忘れていたみたいです．

返信してくださったみなさん本当にありがとうございます．

もう一つの問題のほうを取り組み中です．