サイクロイド
サイクロイド
hajime さんの書込 (2006/06/27(Tue) 18:51)
サイクロイドの加速度を求め,その向きが中心を通ることを示せってどうやればいいのですかね??高校の頃やったような・・・向きを示すのはtanを使えばできると思ったのですが.そしてもう一つx=at,y=bt^2+ct+d(a,b,c,dは定数)であるときの加速度とその向きを求めよっていうおそらく超簡単な問題がイマイチよくわからないのですが.よろしくお願いします.
Re: サイクロイド
yama さんのレス (2006/06/27(Tue) 23:40)
サイクロイドの加速度という意味がよくわかりませんが,直線上を等速度で転がる円周上の1点の加速度のことでしょうか? その場合は,円の中心を原点とし,円とともに(回転はしないで)平行移動する座標系で考えるのが簡単です.この座標系では,円周上の点は等速円運動をするので,その加速度の向きは容易に分かるでしょう. この座標系は,元の座礁系に対して等速度運動をしているので,どちらの座標系でも加速度は同じになります.
2つ目の質問ですが,加速度の成分は
 で計算できます.向きは計算結果からすぐに分かるでしょう.
で計算できます.向きは計算結果からすぐに分かるでしょう.
Re: 無題
yama さんのレス (2006/07/02(Sun) 23:50)
違います.その計算結果は速度の向きです.
( 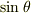 というのも間違っています.正しくは
というのも間違っています.正しくは 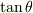 です.)
加速度を求めるのだから2階微分を計算しないといけません.
です.)
加速度を求めるのだから2階微分を計算しないといけません.
無題
hajime さんのレス (2006/07/02(Sun) 23:55)
すいません.LaTeXのコードを使うのにいっぱいいっぱいなもので打ち間違えていました.もちろんタンジェントですよね.では
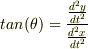 を求めればいいんですよね??
を求めればいいんですよね??
Re: 無題
hajime さんのレス (2006/07/02(Sun) 23:59)
この問題ではxの二回微分が0なんですが・・・解がないということですかね???
Re: 無題
yama さんのレス (2006/07/02(Sun) 23:59)
一般的には 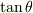 を求めるわけですが,この問題の場合は,成分を見ればすぐに向きが分かるはずです.
を求めるわけですが,この問題の場合は,成分を見ればすぐに向きが分かるはずです.
Re: 無題
hajime さんのレス (2006/07/03(Mon) 00:01)
すいません.まだ物理(数学)をよくわかっていないもので.できたら具体的に教えてもらうことは出来ないでしょうか??
Re: 無題
yama さんのレス (2006/07/03(Mon) 00:07)
ベクトルとして図示してみれば分かると思いますが,x成分が0ということは,加速度はy方向ということです. 向きは,bの正負によってy軸の正または負の向きになります.
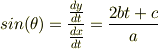
 の向きという解答で正しいでしょうか
の向きという解答で正しいでしょうか