角速度
角速度
mamu さんの書込 (2006/06/27(Tue) 00:25)
一つの直線上を一定の速さVで動く点Pと,直線からLの距離に点Oとがある. 点Pの点Oの周りの角速度を求めてください.また,点Oに関する面積速度を求め,それが一定であることを示せ. 高校三年生の僕にわかりやすく説明してほしいです.
Re: 角速度
mNeji さんのレス (2006/06/27(Tue) 03:30)
点Pが単位時間に進む距離はいつも一定でVになります.点PからV進んだ位置をQとし,三角形OPQを考えると,
点Oから直線までの距離は一定でL.これが三角形OPQの高さ.
一方点Pが直線上の何処にいても,PQ間の長さVは一定で,PQは三角形OPQの底辺のながさ.
故に,三角形OPQが単位時間に張る面積は1/2*L*Vでいつも一定.
Re: 角速度
yama さんのレス (2006/06/27(Tue) 10:04)
角速度は,Oを原点とする極座標でPの位置(r,θ)を表して,dθ/dt を求めればいいと思います.
別の方法として,面積速度を利用して求めることもできます.角速度をωとすると,面積速度は 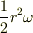 に等しいからです.
r=OP は変化しますが,L,V,tを用いて表しておくといいでしょう.
に等しいからです.
r=OP は変化しますが,L,V,tを用いて表しておくといいでしょう.
Re: 角速度
mamu さんのレス (2006/06/27(Tue) 23:45)
えーっと・・・最後はL,Vであらわすんですよね??うまくいかないので誰か答えを教えてほしいです.
Re: 角速度
yama さんのレス (2006/06/28(Wed) 00:09)
角速度は一定ではなく,時間とともに変化するので,L,V,t で表されることになります.
PがOに最も近づく時刻を0とすると, 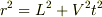 になることに注意しましょう.角速度は最終的には次のようになります.
になることに注意しましょう.角速度は最終的には次のようになります.
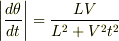
Re: 角速度
mNeji さんのレス (2006/06/28(Wed) 12:55)
話がそれますが,上の式は,以前この掲示板で出ている;
PHYSICさんの「定積分」の式に類似してますね.
例えば,原子核が荷電 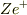 で原点
で原点 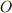 にいて,そこに電子が
にいて,そこに電子が 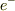 で,速さ
で,速さ  で,原子核の側面を距離
で,原子核の側面を距離  で通り抜ける時に受け取る,横方向のエネルギないしは運動量みたいな計算かも知れないですね.
で通り抜ける時に受け取る,横方向のエネルギないしは運動量みたいな計算かも知れないですね.
お昼時のコント:P)
Re: 角速度
mNeji さんのレス (2006/06/28(Wed) 15:18)
出かける前に気が付いたのでショート・コメントします.
単純にラザフォード散乱の方が考え易いですね.検索の最初に;
Rutherford scattering (Japanese)
が巧みに説明しているようです.
でも,高校の物理・数学の範囲でも近似計算はできるのでは?
Re: 角速度
yama さんのレス (2006/06/28(Wed) 15:20)
どうやらPHYSICさんの「定積分」の式は,電子の軌道を直線と見なした近似計算のようですね.
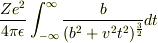 の被積分関数は,そのときに電子が受けるクーロン力の横方向の成分なので,時間で積分すれば,電子が受ける力積の横方向の成分になりますね.縦方向の力積は0なので,これは電子が受ける力積で,運動量変化にも等しいことになりますね.
しかし,運動量が変化すれば,電子の軌道が直線からずれるので,近似であることは明らかですね.
の被積分関数は,そのときに電子が受けるクーロン力の横方向の成分なので,時間で積分すれば,電子が受ける力積の横方向の成分になりますね.縦方向の力積は0なので,これは電子が受ける力積で,運動量変化にも等しいことになりますね.
しかし,運動量が変化すれば,電子の軌道が直線からずれるので,近似であることは明らかですね.
Re: 角速度
mNeji さんのレス (2006/06/28(Wed) 22:58)
yamaさん:
散乱の運動軌道を直線と超近似したとしても,遠方からVの速さで直線上を-無限大からちか原点に近づき,+無限大の方に飛び去るものの,Vに横方向の成分が付いたことと解釈できますね.
mamuさん:
とすると,yamaさんが示されたように,直線運動の間に「横方向の運動量が変化した事だけに着目する」と,散乱後の方向を決まったと解釈しなおせます.従って,散乱に必要な散乱断面積とか微分散乱断面積と言う量が計算できるはずです.
上に示した九州大学のサイトを見て感触を掴んだら,上に説明した超近似散乱法による散乱を計算してみたら面白いかもしれませんね.
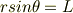
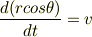
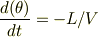
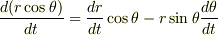 であることに注意しましょう.
であることに注意しましょう.